Получите свидетельство
Вход
ПРЕКРАСНОЕ В МАТЕМАТИКЕ ИЛИ МАТЕМАТИКА В ПРЕКРАСНОМ
«Правильный взгляд на математику открывает не только истину, но и безупречную красоту…»
Бертран Рассел.
Математика – наука о количественных отношениях и пространственных формах действительного мира [1].
Не спорно, математика – это точная наука. Это воплощение порядка и логики. Но нет ни одной области знаний, где не применяется математика. Она помогает понять мир вокруг нас, узнать больше о его законах, так как эти законы подчинены тому же самому порядку, который царит и в математике! Начиная с древних цивилизацией, математика нужна была в любой области, но ее применяли не только в качестве вычислительной науки, но и «математикой занимались ради ее красоты». Математика рассматривалась с эстетической стороны. А что же может быть «прекрасного» в сухих числах и буквах? Но «красота в глазах смотрящего» как говорил Оскар Уайльд.
Часть ученых и исследователей могут называть «красивыми» и «изящными» некоторые теоремы, гипотезы и их решения.
Например, знаменитая формула – тождество Эйлера:
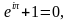где
е – число Эйлера, основание натурального логарифма,
i – мнимая единица, квадрат которой равен «-1»,
π – число «пи».
Эта формула связывает пять фундаментальных математических констант с тремя основными математическими операциями.
Сама формула Эйлера, утверждает, что для любого комплексного числа (действительного числа в частном случае) x выполнено следующее равенство:
[6].
С точки зрения многих математиков эта формула расценивается как красивая, потому что может быть более прекрасным и загадочным, чем взаимодействие мнимых чисел с действительными и в результате получается ноль – ничто.
А некоторые ученые и философы утверждают, что математика подобна искусству. Она сама искусство. И доказательством этому являются, как минимум, 5 «доктрин»:
Симметрия. Мы испытываем восторг, удивление и радость не только, когда видим красоту в окружающих нас вещах – фотографиях, фильмах, пейзажах, людях, предметах высокого искусства, – но и красоту в математике. Что же такое симметрия? Это вид инвариантности, свойство неизменности при некоторых преобразованиях. Например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя центр на месте и при условии, что поверхность тела однородна). Симметрия бывает осевой, центральной, поворотной, зеркальной, зеркально-поворотной, переносной (трансляционной).
Симметрия – основополагающий принцип самоорганизации материальных форм в природе и формообразования в искусстве. Например, приятнее для восприятия любого человека, предмет, созданный по правилам симметрии. Если разделить тело человека вертикальной линией посередине, то левая сторона будет практически симметрична правой. Также, симметрия встречается в природе. Кристаллы, снежинки, падающие дождевые капли (имеющие форму сферы) и многое другое [7].
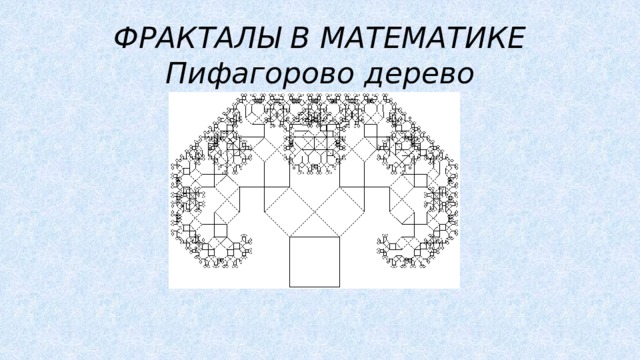
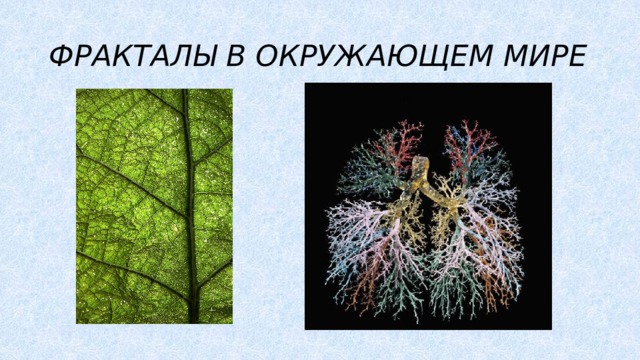
Фракталы. Это множество, которое обладает свойствами самоподобия. Это некий узор, который повторяет сам себя. В математике, например, это множество Кантора или Пифагорово дерево. А в окружающем нас мире – это кораллы, морские звезды или ежи, некоторые цветы и растения (брокколи, капуста), листья деревьев, фрукты и овощи (ананас), снежинки, облака, молнии, а также система кровообращения и бронхи людей и животных [7].
Как оказалась природа фрактала пропитывает не только живую и неживую природу, а также некоторые области искусства. В литературе можно встретить фракталы, которые обладают рядом свойств (некоторая часть произведения подобна целому и восприятие прочитанного происходит по последовательности вложенных уровней). Например, в данном стихотворении видно повторение:
Кто вечно хнычет и скучает —
Тот ничего не замечает,
Кто ничего не замечает —
Тот ничего не изучает,
Кто ничего не изучает,
Тот вечно хнычет и скучает.
Если скучно стало — почитай сначала [5].
Стоит сказать пару слов и о музыке. При изучении темы фракталов талантливый композитор Веркмейстер выявил некоторые свойства: отношение частот одинаковых нот в соседних октавах должно быть равно двум, между этими частотами должно лежать ровно двенадцать нот, по числу полутонов в октаве и все полутона должны быть равны. И впоследствии изучения свойств фракталов и компьютерных технологий появилась компьютерная музыка, которая имеет популярность и на сегодняшний день [3].
Число π. О красоте этого числа можно говорить очень долго. Кто не знает числа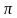 
?В математике мы используем это число для подсчета площади круга, длины окружности или в тригонометрии и других разделах. Это самая настоящая бесконечная периодическая дробь. Но, несмотря на то что о «π» знает каждый, это одно из самых тайных чисел! Швейцарский ученый Петер Трюб, в 2016 году, определил до 22,4 триллиона знаков после запятой. Интересно то, что цифры не складываются в повторяющиеся блоки, поэтому, в числе «π» вы можете найти свой номер телефона. Красота и загадочность бесконечного количества цифр прекрасна!
В книге «Загадочная биография Земли» рассказывается об идеях и исследованиях кандидата географических наук В. Пиотровского. Например, ему удалось установить, что все структуры земного рельефа связаны между собой через число π. Или анализируя контуры знаменитых скрипок Амати, Гварнери, Страдивари, исследователь установил, что можно выделить некоторый объём воздуха в корпусе скрипки. Этот «шар» ровно «в число π» раз укладывается в двух резонаторах инструмента. Интересно, что для рояля, балалайки и гитары присутствие числа «π» не обнаружено. Но эти инструменты и звучат тихо: это камерные инструменты. Корреспондент А. И. Звонков отмечает интересную закономерность у всех растений с овальной формой листьев. Если мысленно разделить лист, например липы, по линии его наибольшей ширины, то левая часть составит примерно трети всей длины. И снова число π. Таких примеров очень много. Почему числу π уделяется столько внимания? Считается. что если правильно рассчитать все цифры, то откроются все тайны мироздания [4].
Золотое сечение. Еще одним известным соотношением является золотое сечение, которое, как говорят ученые, позволяет «размещать предметы самым чудесным образом». Золотое сечение – это пропорция, соотношение двух величин a и b при котором большая величина относится к меньшей, так же как сумма величин к большей, то есть:
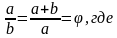
φ – это иррациональное число, коэффициент, которое приблизительно равно «1,6180339887 ……», но обычно используют его сокращенную форму «1,618» [2].
Впервые о нем рассказал древнегреческий математик Евклид. Это соотношение или золотая пропорция считается эталоном «идеальной формы» в архитектуре, искусстве или человеческой фигуре. Применятся в дизайне и фотографии. А также на основе золотого сечения построено исследование типов фигур (яблоко, песочные часы, треугольник, прямоугольник и перевернутый треугольный) [7].
А если снова рассмотреть связь математики и литературы, то можно заметить, как математические законы определяют структуру всего литературного произведения. В композиции стихотворения или произведения золотое сечение проявляется как наличие главного (основного) момента в строке, приходящейся на точку деления общего числа строк стихотворения в золотой пропорции. Хорошим примером служит произведение «Война и мир» Льва Толстого, в самом начале которого, в заглавии закодирован закон золотого сечения. Название романа построено на первых четырех членах ряда Фибоначчи – это 1, 2, 3, 5. Один союз, два существительных, три слова. Пять букв в первом ключевом слове. Отношение ключевых слов 5:3=1,666…, что приблизительно равно коэффициенту φ золотого сечения [5].
Как сказал Г.Лейбниц – «Музыка есть таинственная арифметика души. Она вычисляет, сама того не подозревая». Еще один известный математик Пифагор утверждал, что числа обладают абсолютной властью над всеми событиями, над всеми живыми существами, а значит, числа правят музыкой. Музыка подчиняется высшему закону (математике) и в следствии этого восстанавливает в организме человека гармонию. С помощью математической формулы, Пифагор выяснил, какие пропорции существуют между звуками и какие из них лучше сочетаются между собой. Также, он создал свой музыкальный строй, который назывался Пифагорейским. А также, в музыке можно увидеть золотую пропорцию — конкретное место в музыкальном произведении, где должна быть кульминация [3]. А если присвоить каждой ноте свою цифру, то можно получить определенный ряд чисел, определенную закономерность. В 2007 году группа ученных перевела последовательность Фибоначчи на язык музыки. 17 тыс. из 63 тыс. исследуемых подтвердили, что не слышали более приятной мелодии.
Парадокс Банаха-Тарского. Это теорема которая говорит о том, что любой шар можно разбить на конечное число кусков и составить из них два одинаковых шара того же радиуса, что и исходный. И причем для такого удвоения достаточно разделить шар на пять кусков. Это и является минимумом. Парадокс был открыт в 1926 году Стефаном Банахом и Альфредом Тарским. На практике это невозможно, но в теории очень даже [7].
Математика прекрасна. Математика – это не только строгая система законов, теорем, задач, но и уникальное средство познания красоты. А красота многогранна и многолика. Изучая математику, мы открываем всё новые и новые слагаемые красоты, приближаясь к пониманию, а затем и к созданию красоты и гармонии. Сколько еще неизвестных и неразгаданных истин и открытий? Я рассмотрела лишь малую часть прекрасного в математике, ведь охватить всю красоту науки невозможно.
Список используемых источников:
Википедия. Свободная энциклопедия // Математика [Электронный ресурс] – 2020 – Режим доступа: https://ru.wikipedia.org/wiki/математика – Дата доступа: 05.11.2020.
Википедия. Свободная энциклопедия// Золотое сечение [Электронный ресурс] – 2020 – Режим доступа://https://ru.wikipedia.org/wiki/Золотое_сечение – Дата доступа: 05.11.2020.
Семь восьмых // Музыка и математика [Электронный ресурс] -2020 – Режим доступа: http://earsfingers.ru/chto-obshhego-mezhdu-muzykoj-matematikoj - Дата доступа: 05.11.2020.
Удивительные факты. Сборник самых удивительных фактов, которые могут вас удивить// Факты о числе Пи [Электронный ресурс] – 2019 – Режим доступа: http://amazing-facts.ru/science/fakty_o_chisle_pi.html - Дата доступа: 05.11.2020.
Фестиваль педагогических идей «Открытый урок» // Математика и законы красоты [Электронный ресурс] – 2017 – Режим доступа: https://urok.1sept.ru/articles/682847 - Дата доступа: 05.11.2020.
Хабр // Самая красивая теорема математики: тождество Эйлера [Электронный ресурс] – 2020 – Режим доступа: https://habr.com/ru/post/454136 - Дата доступа: 05.11.2020.
1gai.ru. Первый информационно-развлекательный журнал в России//5 математических феноменов, которые превращают точную науку в эстетическое наслаждение [Электронный ресурс] – 2020 – Режим доступа: https://1gai.ru/baza-znaniy/525248-5-matematicheskih-fenomenov-kotorye-prevraschajut-tochnuju-nauku-v-jesteticheskoe-naslazhdenie.html - Дата доступа: 05.11.2020.
3
Математика в прекрасном (28.18 MB)
0
307
4
Нравится
0
