Математические софизмы

МАТЕМАТИЧЕСКИЕ СОФИЗМЫ

М. А. Мартынюк

Россия, ГОУ ОО СПО «Болховский педагогический колледж»

В математических вопросах нельзя пренебрегать

даже самыми мелкими ошибками.

(И. Ньютон) 

История математики полна неожиданных и интересных софизмов. И зачастую именно их разрешение служило толчком к новым открытиям, из которых, в свою очередь, вырастали новые софизмы. 

Термин «софизм» происходит от греческого слова sophisma, что означает «хитрость». Софизм - это умышленно ошибочное рассуждение, которое выдается за истинное. Чаще всего софизмы являются следствием преднамеренно неправильного подбора исходных положений, двусмысленности слов или подмены понятий.

Логические ошибки в доказательствах и опровержениях, в рассуждении вообще могут допускаться непроизвольно, т.е. без целенаправленного намерения ввести собеседника в заблуждение, или же преднамеренно.
В первом случае такого рода ошибки называются паралогизмами и, как правило, являются следствием невысокой логической культуры.
Второй вид - преднамеренные, замаскированные логические ошибки - называются софизмами.

Известны многие софизмы, дошедшие до нас еще со времен Аристотеля. Например, софизм «Рогатый»: «То, чего ты не терял, ты имеешь. Ты не терял рога. Следовательно, ты имеешь рога».

Аристотель называл софизмом «мнимые доказательства», в которых обоснованность заключения кажущаяся и обязана чисто субъективному впечатлению, вызванному недостаточностью логического анализа. Софистами называли группу древнегреческих философов 4 века до нашей эры, достигших большого искусства в логике. Математический софизм – удивительное утверждение, в доказательстве которого караются незаметные, а подчас и довольно тонкие ошибки. Софизм – это - то же обман, только выполненный намного изящнее и незаметнее, за что мы его и любим. Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в софизмах выполняют «запрещенные» действия или не учитываются условия применимости теорем, формул и правил. В приведенных ниже стихах, взятых из одного английского журнала, выходившего в прошлом веке, рассказывается о хитром хозяине гостиницы, сумевшем разместить в девяти номерах десять гостей так, что каждому из них досталось по отдельной комнате. 

Их было десять чудаков,
Тех спутников усталых,
Что в дверь решили постучать
Таверны «Славный малый».

— Пусти, хозяин, ночевать,
Не будешь ты в убытке,
Нам только ночку переспать,
Промокли мы до нитки.

Хозяин тем гостям был рад,
Да вот беда некстати:
Лишь девять комнат у него
И девять лишь кроватей.

— Восьми гостям я предложу
Постели честь по чести,
А двум придется ночь проспать
В одной кровати вместе.

Лишь он сказал, и сразу крик,
От гнева красны лица:
Никто из всех десятерых
Не хочет потесниться.

Как охладить страстей тех пыл,
Умерить те волненья?
Но старый плут хозяин был
И разрешил сомненья.

Двух первых путников пока,
Чтоб не судили строго,
Просил пройти он в номер «А»
И подождать немного.

Спал третий в «Б», четвертый в «В»,
В «Г» спал всю ночь наш пятый,
В «Д», «Е», «Ж», «3» нашли ночлег
С шестого по девятый.

Потом, вернувшись снова в «А»,
Где ждали его двое,
Он ключ от «И» вручить был рад
Десятому герою.

Хоть много лет с тех пор прошло,
Неясно никому,
Как смог хозяин разместить
Гостей по одному.

Иль арифметика стара,
Иль чудо перед нами,
Понять, что, как и почему,
Вы постарайтесь сами. По характеру ошибок, все софизмы можно разделить на следующие группы: 1. Логические софизмы.

Так как обычно вывод может быть выражен в силлогистической форме, то и всякий софизм может быть сведён к нарушению правил силлогизма. Наиболее типичными источниками логических софизмов являются следующие нарушения правил силлогизма:

• Вывод с отрицательной меньшей посылкой в первой фигуре: «Все люди суть разумные существа, жители планет не суть люди, следовательно, они не суть разумные существа»;

• Вывод с утвердительными посылками во второй фигуре: «Все, находящие эту женщину невинной, должны быть против наказания её; вы — против наказания её, значит, вы находите её невинной»;

• Вывод с отрицательной меньшей посылкой в третьей фигуре: «Закон Моисеев запрещал воровство, закон Моисеев потерял свою силу, следовательно, воровство не запрещено»;

• Особенно распространённая ошибка употребление среднего термина в большой и в меньшей посылке не в одинаковом значении: «Все металлы — простые вещества, бронза — металл: бронза — простое вещество» (здесь в меньшей посылке слово «металл» употреблено не в точном химическом значении слова, обозначая сплав металлов): отсюда в силлогизме получаются четыре термина.

2. Терминологические софизмы.

Грамматические, терминологические и риторические источники софизмов выражаются:

• В неточном или неправильном словоупотреблении и построении фразы. Например, «Все углы треугольника 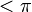» в том смысле, что «каждый угол ».

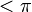• Более сложные софизмы проистекают из неправильного построения целого сложного хода доказательств, где логические ошибки являются замаскированными неточностями внешнего выражения. Например, начав доказывать некоторый тезис, постепенно в ходе доказательства переходят к доказательству другого положения, сходного с тезисом.

3. Психологические софизмы.

Психологические причины софизмов бывают троякого рода: интеллектуальные, аффективные и волевые. Во всяком обмене мыслей предполагается взаимодействие между 2 лицами, читателем и автором или лектором и слушателем, или двумя спорящими. Убедительность софизма поэтому предполагает два фактора: α — психические свойства одной и β — другой из обменивающихся мыслями сторон. Правдоподобность софизма зависит от ловкости того, кто защищает его, и уступчивости оппонента, а эти свойства зависят от различных особенностей обеих индивидуальностей.

4. Интеллектуальные софизмы.

Интеллектуальные причины софизма заключаются в преобладании в уме лица, поддающегося софистике, ассоциаций по смежности над ассоциациями по сходству, в отсутствии развития способности управлять вниманием, активно мыслить, в слабой памяти, непривычке к точному словоупотреблению, бедности фактических знаний по данному предмету, лености в мышлении (ignava ratio) и т. п. Обратные качества, разумеется, являются наиболее выгодными для лица, защищающего софизм: обозначим первые отрицательные качества через , вторые соответствующие им положительные через .

Как было сказано ранее, в математических софизмах чаще всего используются «запрещенные действия» либо не учитываются условия применимости теорем, формул или правил. Часто понимание людьми ошибок в софизме ведет к пониманию математики в целом, развивает логику и навыки правильного мышления. Поиск ошибки в софизме ведет к ее пониманию и осознанию, а осознавая ошибку, человек имеет больше шансов ее не допустить. Также, в истории развития математики софизмы способствовали повышению точности формулировок и более глубокому пониманию понятий математики.

Математические софизмы делятся на арифметические, алгебраические, геометрические и логические.

Рассмотрим несколько примеров алгебраических софизмов, в которых ошибки намеренно скрытые в уравнениях и числовых выражениях.

1. Всякое число равно своему удвоенному значению.

Запишем очевидное для любого числа a тождество
a² - a² = a² - a², вынесем a в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получим a(a – a) = (a + a)(a - a).Разделив обе части на (a – a), получим a = a + a, или a=2a.

Итак, всякое число равно своему удвоенному значению.
Здесь ошибочен переход к равенству a=2a. В самом деле, число a-a, на которое делится равенство a(a – a) = (a + a)(a - a) равно нулю. А мы прекрасно знаем, что на ноль делить нельзя.

2. Чётное число равно нечётному.

Возьмём произвольное чётное число 2n, где n-любое целое число, и запишем тождество ,

в справедливости которого нетрудно убедиться, раскрыв скобки. 

Прибавив к обеим частям этого тождества , перепишем его в следующем виде: , или в таком:,

откуда следует, что , или 2n=2n+1, что означает равенство чётного числа нечётному. Однако из равенства квадратов не следует равенство величин.

3.

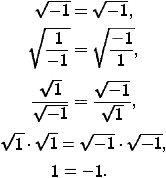
4. Сумма любых двух одинаковых чисел равна нулю. Возьмём произвольное не равное нулю число a и напишем уравнение x=a. Умножая обе его части на (-4а), получим -4ах=. Прибавляя к обеим частям последнего равенства  и перенеся член  влево с противоположным знаком, получим , откуда, замечая, что слева стоит полный квадрат, имеем , или х-2а=х. Заменяя в последнем равенстве х на равное ему число а, получим а-2а=а, или -а=а, откуда 0=а+а, т. е. сумма двух произвольных одинаковых чисел а равна 0. Однако, когда мы имеем полный квадрат , то /х-2а/=/х/, а так x=a, то 2а-x=x.

5. Все числа равны между собой.

Возьмем любые два числа х, у. Рассмотрим тождество х2 – 2ху +у2 =у2 – 2ху +х2. Имеем (х - у)2 = (у – х)2. Отсюда х-у = у-х или 2х= 2у, а, значит, х = у.

Ошибка заключается в том, что из равенства (х - у)2 = (у – х)2 следует, что, а это равенство справедливо для любых чисел у, х.

6. 1=0.

Возьмем уравнение x-a=0. Разделив обе его части на х-а, получим х-а/х-а=0/х-а. Откуда сразу же получаем требуемое равенство 1=0.

Однако в данном софизме используется распространенная ошибка, а именно деление на 0.

7. Всякое число равно своему удвоенному значению.

Запишем очевидное для любого числа а тождество 2а-2а= 2а-2а. Вынесем а в левой части за скобку, а правую часть разложим на множители по формуле разности квадратов, получив: а(а-а)=(а+а)(а-а) (1)

Разделив обе части на а-а, получим а=а+а, а=2а.

В данном софизме вновь используется деление на нуль неравенства (1) (а-а=0 ).

8. Если одно число больше другого, то эти числа равны.

Возьмем два произвольных числа Х и У, такие, что Х У , и другие три произвольных числа а, b и с , сумма которых равна d , т.е. а+ b + c = d . Умножив обе части этого равенства на Х , а затем на У , получим: Хa+Хb+Хc=Хd, Уa+Уb+Уc=Уd. Сложив почленно эти равенства получим Хa + Хb + Хc + Уd = Уa + Уc + Уb + Хd . Перенося здесь Уd  вправо, а  Хd влево, имеем Хa+Хb+ХcХd=Уa+Уb+УcУd.

Вынося слева число Х , а справа число У за скобки, придем к соотношению m(a+b+cd)=n(a+b+cd). (1)

Разделив обе части последнего равенства на ( a + b + c d ) , находим, что, У=Х.

Ошибка, как и в предыдущих примерах заключается в делении на 0, то есть на ( a + b + c d ).

9. Любое число а равно меньшему числу b. 

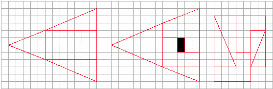Начнем с равенства    а = b + c.

                                                                                                                   

Умножив обе его части на a — b, получим  а² — аb = аb + аc — b² — be.
Перенесем ас в левую часть:  а² — аb — аc = аb — b² — be
 и разложим на множители:  а(а — b — c) = b(а — b — c).
Разделив обе части равенства на а — b — c, найдем  а = b,   что и требовалось доказать.

Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда. Рассмотрим некоторые из арифметических софизмов.

1. Дважды два – пять.

Пусть исходное соотношение - очевидное равенство: 4:4= 5:5 (1) .

Вынесем за скобки общий множитель каждой чести (1) равенства, и мы получим: 4*(1:1)=5*(1:1). (2)

Разложим число 4 на произведение 2 *2.

(2*2)* (1:1)=5*(1:1).  (3)

Наконец, зная, что 1:1=1, мы из соотношения (2) устанавливаем: 2*2=5.

Ошибка заключается в том, что нельзя было выносить множитель за скобки в уравнение (2).

2. Один рубль не равен ста копейкам.

Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. Если a=b, c=d, то ac=bd. 

Применим это положение к двум очевидным равенствам 1 р.=100 коп, (1)

10р.=10*100коп. (2) 

Перемножая эти равенства почленно, получим 10 р.=100000 коп.

Наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп., таким образом, один рубль не равен ста копейкам.

Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.

3. Число, равное другому числу, одновременно и больше, и меньше его.

Возьмем два положительных равных числа a и b и напишем для них следующие неравенства: 

a - b и b - b. 

Перемножив оба этих неравенства почленно, получим неравенство a·bb·b. 

Разделим его на b (это законно, т.к. b0), получим a b. 

Записав же два других столь же бесспорных неравенства:

b - a и  a - a.

Перемножив оба этих неравенства почленно, получим неравенство b·a a·a. 

Разделив на a0, придем к b a. 

Итак, число a, равное числу b, одновременно и больше, и меньше его. 

Ошибка заключается в неправильном почленном перемножении, вследствие которого место выражений a-b; b-a получились выражения ab; a .

4. 1=2.

Никто не станет возражать, что 3-1=6-4. Умножим обе части равенства на (-1): 1-3=4-6, прибавим к обеим частям равенства одно и тоже число, (9/4):1-3+9/4=4-6 +9/4.

Замечаем, что обе части равенства представляют собой квадраты разностей: (1-3/2)2=(2-3/2)2.

Извлечем из обеих частей квадратный корень: 1-3/2=2-3/2, и теперь к каждой части прибавим 3/2, имеем 1=2.

Не менее интересными являются геометрические софизмы, которые основаны на ошибках связанных с геометрическими фигурами и действиями над ними. В качестве примера, рассмотрим следующие софизмы.

1. Спичка вдвое длиннее телеграфного столба.

Пусть, а дм - длина спички и b дм - длина столба. Разность между b и a обозначим через c . Имеем b - a = c, b = a + c. Перемножаем два эти равенства по частям, находим: 2b - ab = ca + 2c. Вычтем из обеих частей bc. Получим: 2b- ab - bc = ca + 2c - bc, или b(b - a - c) = - c(b - a - c), откуда b = - c, но c = b - a, поэтому b = a - b, или a = 2b.  Тем не менее, в выражении b(b-a-c)=(-c)*(b-a-c) производится деление на (b-a-c), а этого делать нельзя, так как b-a-c=0.Значит, спичка не может быть вдвое длиннее телеграфного столба.

2. Хорда, не проходящая через центр окружности, равна диаметру.

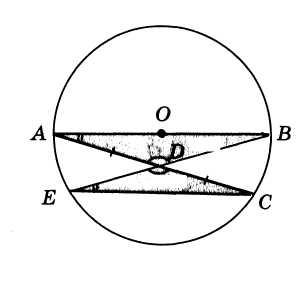
Пусть в окружности приведен диаметр АВ. Через точку В проведем любую хорду ВЕ, не проходящую через центр, затем через середину этой хорды D и точку А проведем новую хорду АС. Наконец, точки Е и С соединим отрезком прямой. Рассмотрим ∆АВD и ∆ЕDС.

В этих треугольниках: ВD = DЕ (по построению), А=Е (как вписанные, опирающиеся на одну и ту же дугу).

Кроме того,  ВDА=ЕDC (как вертикальные). Если же сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны. Значит, ∆ ВDА= ∆ЕDC , а в равных треугольниках против равных углов лежат равные стороны. Поэтому, АВ=ЕС. 

По теореме о признаке равенства треугольника:

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

А в нашем случае, А не прилежит к стороне ВD .

Ошибка заключается в неправильном применении теоремы о равенстве треугольников (равны 2 угла , не прилежащие к одной стороне).

3. Тор.

 

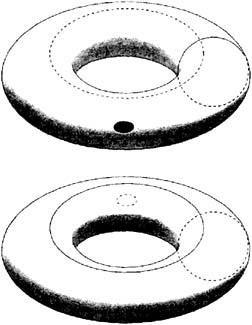
Один из наиболее впечатляющих софизмов топологии заключается в том, что тор (поверхность  бублика), если его поверхность растягивать (не разрывая при этом), можно вывернуть наизнанку  через любую сколь угодно малую дырочку. Никакой проблемы здесь нет. Но уж если тор  действительно можно вывернуть наизнанку, то следует  обратить внимание и еще на один, пожалуй, даже более удивительный факт.  Если тор вывернуть наизнанку, то кажется, что кольца, нарисованные на его поверхности, расцепляются.

  На наружной стороне тора проведем меридиан (рис, вверху). На внутренней стороне того же тора проведем параллель. Обе эти окружности, очевидно, сцеплены между собой. Вывернем теперь тор наизнанку через дырочку в его поверхности. Как видно из нижнего рисунка, первая окружность перейдет с наружной поверхности тора внутрь, а вторая — наружу, и обе окружности окажутся расцепленными. Очевидно, что это нарушает фундаментальный топологический закон, который гласит: разделить две сцепленные замкнутые кривые можно, лишь разорвав одну из кривых и протащив через место разрыва вторую.

4. Из точки на прямой можно опустить два перпендикуляра.

Попытаемся «доказать», что через точку, лежащую вне прямой, к этой прямой можно провести два перпендикуляра.

С этой целью возьмем треугольник АВС. На сторонах АВ и ВС этого треугольника, как на диаметрах, построим полуокружности.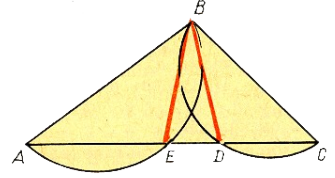

Пусть эти полуокружности пересекаются со стороной АС в точках Е и D. Соединим точки Е и D прямыми с точкой В.

Угол АЕВ прямой, как вписанный, опирающийся на диаметр; угол ВDС также прямой. Следовательно, ВЕ перпендикулярна АС и ВD перпендикулярна АС. Через точку В проходят два перпендикуляра к прямой АС.

Особый интерес с момента зарождения математики, как одной из фундаментальных наук, вызывали логические софизмы. Логические софизмы - софизмы, ошибки которых заключаются в неправильных рассуждениях.

1. Софизм Кратила. Диалектик Гераклит, провозгласив тезис «все течет», пояснял, что в одну и ту же реку (образ природы) нельзя войти дважды, ибо когда входящий будет входить в следующий раз, на него будет течь уже другая вода. Его ученик Кратил, сделал из утверждения учителя другие выводы: в одну и ту же реку нельзя войти даже один раз, ибо пока ты входишь, она уже изменится. Поэтому Кратил предлагал не называть вещи, а указывать на них: пока произносишь название, вещь уже станет иной.

2. Полупустое и полуполное.

Полупустое есть то же, что и полуполное. Если равны половины, значит, равны и целые. Следовательно, пустое есть то же, что и полное

Однако полупустое не является половиной чего либо пустого, а является чем либо наполовину наполненным.

3. Вор.

Вор не желает приобрести ничего дурного. Приобретение хорошего есть дело хорошее. Следовательно, вор желает хорошего.

4. Не знаешь то, что знаешь.

«Знаешь ли ты, о чём я хочу тебя спросить?» — «Нет». — «Знаешь ли ты, что добродетель есть добро?» — «Знаю». — «Об этом я и хотел тебя спросить. А ты, выходит, не знаешь то, что знаешь».

5. Лекарства.

«Лекарство, принимаемое больным, есть добро. Чем больше делать добра, тем лучше. Значит, лекарств нужно принимать как можно больше».

6. Отец — собака.

«Эта собака имеет детей, значит, она — отец. Но это твоя собака. Значит, она твой отец. Ты её бьёшь, значит, ты бьёшь своего отца и ты — брат щенят».

Как видно из приведённых выше софизмов, найти ошибки в них не очень сложно, зная основные математические законы и их доказательства. Однако можно выделить несколько основных способов нахождения ошибки в софизме:

• Внимательно прочитать условие предложенной вам задачи. Начинать поиск ошибки лучше с условия предложенного софизма. В некоторых софизмах абсурдный результат, получается, из-за противоречивых или неполных данных в условии, неправильного чертежа, ложного первоначального предположения, а далее все рассуждения проводятся верно. Это и вызывает затруднения при поиске ошибки. Все привыкли, что задания, предполагаемые в различной литературе, не содержат ошибок в условии и, поэтому, если получается неверный результат, то ошибку они ищут непременно по ходу решения.

• Установите области знаний (темы), которые отражены в софизме, предложенных преобразованиях. Софизм может делиться на несколько тем, которые потребуют детального анализа каждой из них.

• Выясните, соблюдены ли все условия применимости теорем, правил, формул, соблюдена ли логичность. Некоторые софизмы построены на неверном использовании определений, законов, на «забывании» условий применимости. Очень часто в формулировках, правилах запоминаются основные, главные фразы и предложения, всё остальное упускается. И тогда второй признак равенства треугольников превращается в признак «по стороне и двум углам».

• Проверяйте результаты преобразования обратным действием.

• Часто следует разбить работу на небольшие блоки и проконтролировать правильность каждого такого блока.

Можно бесконечно говорить о софизмах в целом и о математических софизмах в частном. Из года в год появляются новые софизмы, некоторые из них могут остаться в истории, о многих быстро забудут. Ведь софизмы - это смесь математики и логики, поэтому они помогают не только развивать логику, но и лучше понимать математику в целом. В современном мире есть много людей, так или иначе употребляющих софизмы в обычной жизни, даже не зная, что это такое. Есть же и такие люди, которые целенаправленно изучают софизмы, например политики или СМИ, чтобы вводить людей в заблуждение, или просто развить свои навыки логики и правильности рассуждений.

Поначалу может показаться, что существует мало софизмов, или, что они не используются в жизни, то есть бесполезны. Но это не так. Существует огромное множество разных видов софизмов. И математические софизмы – всего лишь небольшая их часть. За свою жизнь человек слышит десятки софизмов, не умея отличить их от правдивых утверждений, и даже не зная, что вообще означает слово софизм.

Понять софизм, то есть решить его, получается не сразу. Поначалу, чтобы решить некоторые софизмы, приходится по многу раз их внимательно перечитывать, вдумываться и всматриваться. В ходе написания данной работы и доказательства софизмов, приведённых в ней, ошибки стали находиться быстрее. Хорошо развитое логическое мышление может помочь не только в решении задач, но и в обычной жизни.

О математических софизмах можно говорить бесконечно много, как и о математике в целом. Изо дня в день рождаются новые парадоксы, некоторые из них останутся в истории, а некоторые просуществуют один день

Вообще, решение софизмов – интересное и познавательное занятие. Им можно заниматься как целенаправленно, так и в свободное время для собственного удовольствия. Изучение математических софизмов раскрывает еще одну страничку в математике, позволяет прикоснуться к тому, с чем сталкивались далекие предки, к теме, которая имеет исторические корни.

Литература

1. Брадис В. М., Минковский В. Л., Харчева Л. К. Ошибки в математических рассуждениях. 3 изд.: М., 1967.
2. Дёмин Р. Н. Собрание «задач» Ричарда Софиста как контекст для «парадоксов» древнекитайской школы имен // Вестник РХГА № 6, СПб., 2005.
3. Ивин А. А.. Логика.: М. - Издательство «Знание», Изд. 2-е, 1998. 
4. Интернет источник Timerl@n.

5. Интернет источник http://www.rchgi.spb.ru/Pr/vest_6.htm.

6. Неркарарян К. В., Софизмы и парадоксы, 1 издание, 2001.