Цель: повышение интереса обучающихся к математике, расширение кругозора обучающихся. развитие познавательных способностей, воспитание ответственного отношения к делу, умения внимательно слушать сверстников.
Оформление: плакат «Математика- царица наук» (К.Гаусс).
Ход мероприятия
1 ведущий. Добрый день всем! Сегодня у нас устный журнал «Ай да математика!» Любой журнал- это источник информации, который содержит статьи по разным направлениям. На «страницах» нашего журнала вы узнаете много интересного о математике.
2 ведущий. Будьте внимательны и собраны. Вам придётся не только слушать, но и отвечать на вопросы, решать задачи, считать и даже играть. А самых активных участников журнала ждут награды. А помогут вам знания, полученные на уроках, плюс смекалка, находчивость и логика.
1 страница. «По страницам истории математики»
1 ведущий. Сколько великих людей восхищались математикой! «Математика- царица наук», «Математика в порядок ум приводит»… Математику некоторые считают сложной наукой. Но многие и не догадываются о том, как можно легко и даже весело заниматься математикой. Французский писатель 19 столетия Анатоль Франс однажды заметил: «Учиться можно весело… Чтобы переваривать знания, надо поглощать их с аппетитом».
2 ведущий. А французский император Наполеон говорил: «Процветание и совершенствование математики тесно связано с благосостоянием государства».
1 ведущий. Видимо, от понимания этого обстоятельства в Париже есть улицы, носящие имена выдающихся математиков. Это улицы Летандра, Реомюра, Паскаля, Бюффона, Карно, Декарта, Лейбница.
2 ведущий. Математики- кто они? О них рассказывают столько небылиц. Например, гуляя, Пифагор подошёл к реке. Река тот час же вышла из берегов и закричала (!): «Да здравствует Пифагор!».
1 ведущий. Однажды Шерлок Холмс и его неизменный спутник Ватсон отправились в путешествие на воздушном шаре. Сильный ветер погнал их шар в неизвестном направлении. Затем ветер несколько унялся, и они приземлились в пустынной и загадочной местности.
Вскоре, однако, они заметили приближающегося к ним человека.
- Не могли бы вы, хотя бы приблизительно, сказать нам, где мы находимся? -спросил его Холмс.
Человек задумался на некоторое время и затем ответил:
- Почему приблизительно? Я могу ответить абсолютно точно. Вы находитесь в гондоле воздушного шара.
Очередной порыв ветра понес шар дальше в неизвестном направлении.
- Черт бы побрал этих математиков! - раздраженно проговорил Шерлок Холмс, - А почему вы считаете, что этот человек был математиком? - как всегда удивился Ватсон.
- Ну, во-первых, прежде чем ответить, он подумал, а во- вторых, его ответ был абсолютно точен и абсолютно бесполезен для нас.
2 страница. «Исторические задачи»
1 ведущий. Рассказывают, что в начальной школе, где учился мальчик Карл Гаусс, ставший потом знаменитым математиком, учитель, чтобы занять класс на продолжительное время самостоятельной работой дал детям задание- вычислить сумму всех натуральных чисел от 1 до 100. Но маленький Гаусс это задание выполнил почти моментально. Попробуйте и вы быстро выполнить это задание.
2 ведущий. Когда индийский царь Шерам узнал об удивительной игре в шахматы, он приказал позвать к себе её изобретателя- учёного Сету.
Царь пообещал наградить бедного учёного, чем тот сам пожелает. Сета попросил в награду за своё изобретение столько пшеничных зёрен, сколько получится, если на первую клетку шахматной доски положить одно зерно, на вторую- в 2 раза больше, т.е. 2 зерна, на третью- ещё в 2 раза больше, т.е. 4 (22 ) ), на четвертую—еще в 2 раза больше, т. е. 8 (23) зёрен и т. д. до 64-й клетки.
Царь подивился такой скромности ученого и велел слугам принести Сете мешок требуемой пшеницы. Слуги ушли, но... выполнить просьбу Сеты они не смогли. Почему же? Подсчитаем, сколько всего зерен должны были выдать Сете в награду за изобретение шахмат. Нужно найти сумму:
5==1+21+22+23+24+...+262+263.
64 слагаемых
Можно непосредственно найти значение суммы. Но это займет очень много времени. А можно попробовать оценить величину этой суммы, сравнив её с каким-нибудь числом. Очевидно, что сумма S больше, чем каждое из слагаемых, ее составляющих. Вот и давайте считать, что S больше последнего слагаемого 263 , и найдем значение 263:
263=260•23==(210)6•8=10246•8=(10242)3•8==(1048576)3 * 8=9 223 372 036 854 775 808.
Не может быть, такое количество зёрен действительно уместится в мешке (ведь зерно очень маленькое по размеру)?
Известно, что куб, ребро которого равно 1 м (так называемый кубический метр), вмещает около 15 млн. зерен пшеницы. Теперь подсчитайте, сколько таких кубических метров, заполненных зёрнами, нужно поставить друг на друга, чтобы в них поместилось требуемое количество зерен. Какова будет высота такой «башни»? (Для сравнения скажем, что среднее расстояние от Земли до Солнца равно 150 000 000 км.)
1 ведущий. Пифагор – один из величайших математиков Древней Греции. У Пифагора была своя школа. Рассмотрим задачу! У Пифагора спросили, сколько учеников в его школе. Он ответил: «Половина учеников изучает математику, четвёртая часть – музыку, седьмая часть – молчит, и кроме того есть ещё 3 женщины». Сколько учеников в школе Пифагора?
Решение:
1) 1/2 + 1/4 + 1/7 = 25/28
2) 1 - 25/28 = 3/28 – всех учеников приходится на женщин
3) 3 : 3 · 28 = 28 (уч) – в школе Пифагора
3 страница. «Математические софизмы».
1 ведущий. Верно ли данное равенство: 5 = 4?
Вы, конечно, ответите: «Нет!». Но попробуем доказать, что 5 = 4.
Пусть х = 1/3, тогда 3х = 1. Представим 3х как 15х – 12х, а 1 – как 5 – 4, тогда вместо равенства 3х = 1 можно записать
15х – 12х = 5 – 4.
Решим это уравнение:
15х – 5 = 12х – 4,
5(3х – 1) = 4(3х – 1).
Разделим обе части равенства на (3х – 1) и получим 5 = 4..
Где в рассуждениях мы допустили ошибку?
Ошибку мы допустили в том шаге рассуждений при решении уравнения, где обе части равенства 5(3х – 1) = 4(3х – 1) разделили на (3х – 1).
По нашему предположению, сделанному в начале рассуждений, х = 1/3, т.е. 3х = 1, или 3х – 1 = 0. Мы обе части уравнения разделили на 0, что делать нельзя.
2 ведущий. Софизм- последовательность высказываний, содержащих скрытую ошибку, за счёт чего удаётся сделать неправдоподобный вывод. Обычно в математических софизмах скрыто выполняются запрещённые действия или нарушаются условия применения правил или теорем. Задача заключается в том, чтобы найти ошибку в рассуждениях.
1 ведущий. Предлагаем ещё один софизм.
Умножим обе части равенства на с и получим с* b = с2. От обеих частей отнимем b2:
с b – b2 = с2 – b2. Разложим на множители левую и правую части последнего равенства:
b( с – b) = (с – b) (с + b). Разделим обе части на (с – b), получим b = с + b; так как по условию с = b, то b = b + b, т.е. b = 2b
Где была допущена ошибка?
4 страница. Математические настольные игры.
В игре участвуют любое количество человек. Играть можно как на улице, так и дома. Если игра проходит на улице, то чертят на земле несколько окружностей и присваивают центральному кругу и каждому кольцу определённое число: положительное, отрицательное или нуль, как, например, на рис.1.
Все играющие набирают себе по одинаковому количеству бит (камешков). Первый по жребию бросает свои биты и в зависимости от попадания в то или иное кольцо считает сумму набранных им очков ( в нашем случае это -8 + (-6) * 2 + 3 + 9 = -8). Затем то же проделывают другие игроки. Победит тот, кто не только наберёт большее количество очков, но и не ошибётся при подсчёте их количества.
Если играют дома, то чертят аналогичные круги циркулем на большом листе бумаги. На этом же листе проводят прямую линию (рис. 2) и за ней выстраивают фишки (ими могут служить, например, пуговицы, монеты, шашки), которые направляют в круги щелчками.
5 страница. «Математические ребусы»
1 ведущий. Наверное, все вы умеете разгадывать ребусы. Мы будем разгадывать математические ребусы, но сначала их придумывать.
2 ведущий. Вот я придумал такой. Кто его отгадает?
1 ведущий. Парабола! А теперь придумайте ребусы вы!
6 страница. Ускоренный и упрощённый счёт.
1 ведущий. Давайте учиться быстрому счёту!
1.Умножение и деление на 4.
Чтобы число умножить на 4, его дважды удваивают. Например:
213 * 4 = (213 * 2) * 2= 426 * 2= 852.
Чтобы число разделить на 4, его дважды делят на 2. Например:
124 : 4= (124 : 2) : 2= 62 : 2= 31.
2.Умножение на 5.
Чтобы умножить число на 5, нужно умножить его на 10/2, т.е. умножить на 10 и разделить на 2. Например:
138 * 5=(138*10):2=1380:2=690.
3.Умножить на 25.
Чтобы число умножить на 25, нужно его умножить на 100/4, т.е. умножить на 100 и разделить на 4. Например:
348*25=34800:4=8700.
4.Умножить на1,5.
Чтобы число умножить на 1,5, надо к исходному числу прибавить половину. Например:
24*1,5=24+12=36;
129*1,5=129+64,5=193,5.
5.Умножение на 9.
Чтобы число умножить на 9, к нему приписывают ноль и отнимают исходное число. Например, 241*9=2410-241=2169.
6. Умножение на 11.
Чтобы умножить число на 11, к нему приписывают ноль и прибавляют исходное число. Например: 241*11=2410+241=2651.
Упражняясь в вычислениях, вы можете сами составить другие алгоритмы ускоренного и упрощённого счёта.
В заключение ведущий подводит итоги, награждает самых активных участников журнала медалями «Лучший математик».

 Получите свидетельство
Получите свидетельство Вход
Вход


 арь подивился такой скромности ученого и велел слугам принести Сете мешок требуемой пшеницы. Слуги ушли, но... выполнить просьбу Сеты они не смогли. Почему же? Подсчитаем, сколько всего зерен должны были выдать Сете в награду за изобретение шахмат. Нужно найти сумму:
арь подивился такой скромности ученого и велел слугам принести Сете мешок требуемой пшеницы. Слуги ушли, но... выполнить просьбу Сеты они не смогли. Почему же? Подсчитаем, сколько всего зерен должны были выдать Сете в награду за изобретение шахмат. Нужно найти сумму: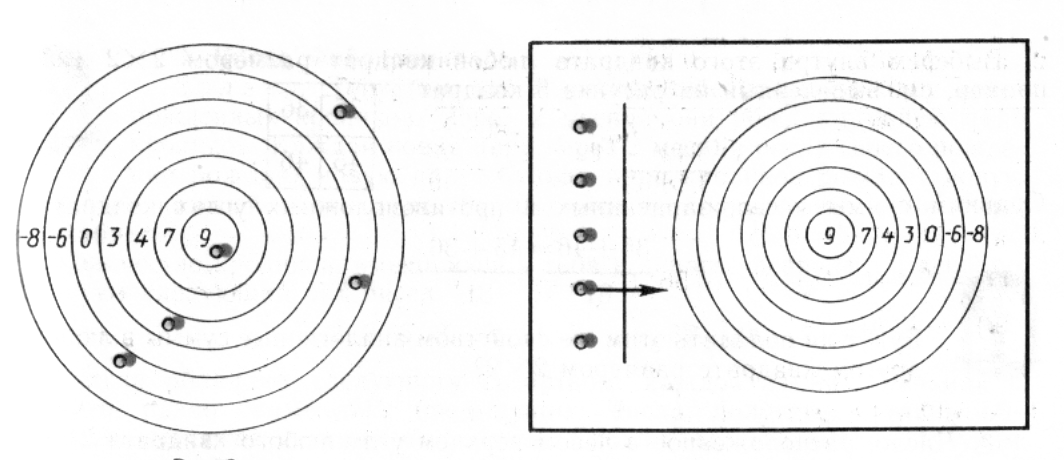














 Ай да математика! (1.09 MB)
Ай да математика! (1.09 MB)
 0
0 747
747 46
46 Нравится
0
Нравится
0


