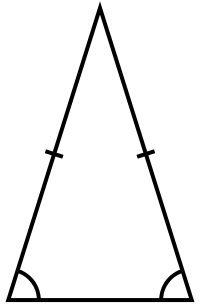
Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя — основанием.
По определению, правильный треугольник также является равнобедренным, но обратное утверждение неверно.
Свойства.
Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой. Также равны биссектрисы, медианы и высоты, проведённые из этих углов.
Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию, совпадают между собой. Центры вписанной и описанной окружностей лежат на этой линии.
Пусть a — длина двух равных сторон равнобедренного треугольника, b — длина третьей стороны, h — высота равнобедренного треугольника.

a = b/2cosα (следствие теоремы косинусов)
b = 2acosα (теорема о проекциях)
b = 2asinβ/2
Радиус вписанной окружности может быть выражен шестью способами в зависимости от того, какие два параметра равнобедренного треугольника известны.
Углы могут быть выражены следующими способами:
α = (П - β) /2
β = П - 2α
α = arcsina/2R
β = arcsinb/2R.
Угол может также найден без П и R. Треугольник делится медианой пополам, и в полученных 2-х равных прямоугольных треугольниках вычисляется углы:
y = cosα = b/c, arccos y = x.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


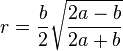
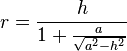
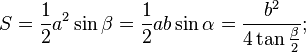
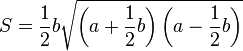 .
.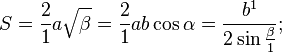









 Материал по математике "Равнобедренный треугольник" (42.64 КB)
Материал по математике "Равнобедренный треугольник" (42.64 КB)
 0
0 357
357 5
5 Нравится
0
Нравится
0





