Материал по математике по теме "Сюжетные задачи"

Задачи:

1. В трёх вер­ши­нах квад­ра­та на­хо­дят­ся три куз­не­чи­ка. Они иг­ра­ют в че­хар­ду, т. е. пры­га­ют друг через друга. При этом, если куз­не­чик A пры­га­ет через куз­не­чи­ка B, то после прыж­ка он ока­зы­ва­ет­ся от B на том же рас­сто­я­нии, что и до прыж­ка, и, есте­ствен­но, на той же пря­мой. Может ли один из них по­пасть в четвёртую вер­ши­ну квад­ра­та?

2. Два иг­ро­ка ходят по оче­ре­ди. Перед на­ча­лом игры у них есть по­ров­ну го­ро­шин. Ход со­сто­ит в пе­ре­да­че со­пер­ни­ку лю­бо­го числа го­ро­шин. Не раз­ре­ша­ет­ся пе­ре­да­вать такое ко­ли­че­ство го­ро­шин, ко­то­рое до этого уже кто‐то в этой пар­тии пе­ре­да­вал. Ноль го­ро­шин тоже пе­ре­да­вать нель­зя. Тот, кто не может сде­лать оче­ред­ной ход по пра­ви­лам, — счи­та­ет­ся про­иг­рав­шим. Кто — на­чи­на­ю­щий или его со­пер­ник — по­бе­дит в этой игре, как бы ни играл его партнёр?

Рас­смот­ри­те слу­чаи:

а) У каж­до­го по две го­ро­ши­ны;

б) У каж­до­го по три го­ро­ши­ны;

в) Общий слу­чай: у каж­до­го по N го­ро­шин.

3. Трое дру­зей иг­ра­ли в шашки. Один из них сыг­рал 25 игр, а дру­гой — 17 игр. Мог ли тре­тий участ­ник сыг­рать

а) 34;

б) 35;

в) 56 игр?

4. Леша за­ду­мал дву­знач­ное число (от 10 до 99). Гриша пы­та­ет­ся его от­га­дать, на­зы­вая дву­знач­ные числа. Если Гриша пра­виль­но на­зы­ва­ет число, или же одну цифру на­зы­ва­ет пра­виль­но, а в дру­гой оши­ба­ет­ся не более чем на еди­ни­цу, то Леша от­ве­ча­ет «тепло»; в осталь­ных слу­ча­ях Леша от­ве­ча­ет «хо­лод­но». (На­при­мер, если за­ду­ма­но число 65, то на­звав 65, 64, 66, 55 или 75, Гриша услы­шит в ответ «тепло», а в осталь­ных слу­ча­ях услы­шит «хо­лод­но». )

а) По­ка­жи­те, что нет спо­со­ба, при ко­то­ром Гриша га­ран­ти­ро­ван­но узна­ет число, ис­тра­тив 18 по­пы­ток.

б) При­ду­май­те спо­соб, при ко­то­ром Гриша га­ран­ти­ро­ван­но узна­ет число, ис­тра­тив 24 по­пыт­ки (какое бы число ни за­ду­мал Леша).

в) А за 22 по­пыт­ки по­лу­чит­ся?

5. В бо­та­ни­че­ском спра­воч­ни­ке каж­дое рас­те­ние ха­рак­те­ри­зу­ет­ся 100 при­зна­ка­ми (каж­дый при­знак либо при­сут­ству­ет, либо от­сут­ству­ет). Рас­те­ния счи­та­ют­ся "не­по­хо­жи­ми", если они раз­ли­ча­ют­ся не менее, чем по 51 при­зна­ку.

а) По­ка­жи­те, что в спра­воч­ни­ке не может на­хо­дить­ся боль­ше 50 по­пар­но не­по­хо­жих рас­те­ний.

б) А может ли быть 50?

Полную информацию смотрите в файле. 

Сюжетные задачи

1. В трёх вер­ши­нах квад­ра­та на­хо­дят­ся три куз­не­чи­ка. Они иг­ра­ют в че­хар­ду, т. е. пры­га­ют друг через друга. При этом, если куз­не­чик A пры­га­ет через куз­не­чи­ка B, то после прыж­ка он ока­зы­ва­ет­ся от B на том же рас­сто­я­нии, что и до прыж­ка, и, есте­ствен­но, на той же пря­мой. Может ли один из них по­пасть в четвёртую вер­ши­ну квад­ра­та?

2. Два иг­ро­ка ходят по оче­ре­ди. Перед на­ча­лом игры у них есть по­ров­ну го­ро­шин. Ход со­сто­ит в пе­ре­да­че со­пер­ни­ку лю­бо­го числа го­ро­шин. Не раз­ре­ша­ет­ся пе­ре­да­вать такое ко­ли­че­ство го­ро­шин, ко­то­рое до этого уже кто‐то в этой пар­тии пе­ре­да­вал. Ноль го­ро­шин тоже пе­ре­да­вать нель­зя. Тот, кто не может сде­лать оче­ред­ной ход по пра­ви­лам, — счи­та­ет­ся про­иг­рав­шим. Кто — на­чи­на­ю­щий или его со­пер­ник — по­бе­дит в этой игре, как бы ни играл его партнёр?

Рас­смот­ри­те слу­чаи:

а) У каж­до­го по две го­ро­ши­ны;

б) У каж­до­го по три го­ро­ши­ны;

в) Общий слу­чай: у каж­до­го по N го­ро­шин.

3. Трое дру­зей иг­ра­ли в шашки. Один из них сыг­рал 25 игр, а дру­гой — 17 игр. Мог ли тре­тий участ­ник сыг­рать  

а) 34;

б) 35;

в) 56 игр?

4. Леша за­ду­мал дву­знач­ное число (от 10 до 99). Гриша пы­та­ет­ся его от­га­дать, на­зы­вая дву­знач­ные числа. Если Гриша пра­виль­но на­зы­ва­ет число, или же одну цифру на­зы­ва­ет пра­виль­но, а в дру­гой оши­ба­ет­ся не более чем на еди­ни­цу, то Леша от­ве­ча­ет «тепло»; в осталь­ных слу­ча­ях Леша от­ве­ча­ет «хо­лод­но». (На­при­мер, если за­ду­ма­но число 65, то на­звав 65, 64, 66, 55 или 75, Гриша услы­шит в ответ «тепло», а в осталь­ных слу­ча­ях услы­шит «хо­лод­но».)

а) По­ка­жи­те, что нет спо­со­ба, при ко­то­ром Гриша га­ран­ти­ро­ван­но узна­ет число, ис­тра­тив 18 по­пы­ток.

б) При­ду­май­те спо­соб, при ко­то­ром Гриша га­ран­ти­ро­ван­но узна­ет число, ис­тра­тив 24 по­пыт­ки (какое бы число ни за­ду­мал Леша).

в) А за 22 по­пыт­ки по­лу­чит­ся?

5. В бо­та­ни­че­ском спра­воч­ни­ке каж­дое рас­те­ние ха­рак­те­ри­зу­ет­ся 100 при­зна­ка­ми (каж­дый при­знак либо при­сут­ству­ет, либо от­сут­ству­ет). Рас­те­ния счи­та­ют­ся "не­по­хо­жи­ми", если они раз­ли­ча­ют­ся не менее, чем по 51 при­зна­ку.

а) По­ка­жи­те, что в спра­воч­ни­ке не может на­хо­дить­ся боль­ше 50 по­пар­но не­по­хо­жих рас­те­ний.

б) А может ли быть 50?

6. 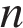школь­ни­ков хотят раз­де­лить по­ров­ну оди­на­ко­вых шо­ко­ла­док, при этом

каж­дую шо­ко­лад­ку можно раз­ло­мить не более од­но­го раза.

а) При каких 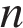это воз­мож­но, если

б) При каких 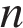и это воз­мож­но?

7. Даны N синих и N крас­ных па­ло­чек, при­чем сумма длин синих па­ло­чек равна сумме длин крас­ных. Из­вест­но, что из синих па­ло­чек можно сло­жить N‐уголь­ник, и из крас­ных — тоже. Все­гда ли можно вы­брать одну синюю и одну крас­ную па­лоч­ки и пе­ре­кра­сить их (синюю — в крас­ный цвет, а крас­ную — в синий) так, что снова из синих па­ло­чек можно будет сло­жить N‐уголь­ник, и из крас­ных — тоже?

Ре­ши­те за­да­чу

а) для N = 3;

б) для про­из­воль­но­го на­ту­раль­но­го N 3.

8. а) Ску­пой ры­царь хра­нит зо­ло­тые мо­не­ты в шести сун­ду­ках. Од­на­ж­ды, пе­ре­счи­ты­вая их, он за­ме­тил, что если от­крыть любые два сун­ду­ка, то можно раз­ло­жить ле­жа­щие в них мо­не­ты по­ров­ну в эти два сун­ду­ка. Еще он за­ме­тил, что если от­крыть любые 3, 4 или 5 сун­ду­ков, то тоже можно пе­ре­ло­жить ле­жа­щие в них мо­не­ты таким об­ра­зом, что во всех от­кры­тых сун­ду­ках ста­нет по­ров­ну монет. Тут ему по­чу­дил­ся стук в дверь, и ста­рый скря­га так и не узнал, можно ли раз­ло­жить все мо­не­ты по­ров­ну по всем шести сун­ду­кам. Можно ли, не за­гля­ды­вая в за­вет­ные сун­ду­ки, дать точ­ный ответ на этот во­прос?

б) А если сун­ду­ков было во­семь, а cку­пой ры­царь мог раз­ло­жить по­ров­ну мо­не­ты, ле­жа­щие в любых 2, 3, 4, 5, 6 или 7 сун­ду­ках?

9. За круг­лым сто­лом сидят 4 гнома. Перед каж­дым стоит круж­ка с мо­ло­ком. Один из гно­мов пе­ре­ли­ва­ет ¼ сво­е­го мо­ло­ка со­се­ду спра­ва. Затем сосед спра­ва де­ла­ет то же самое. Затем то же самое де­ла­ет сле­ду­ю­щий сосед спра­ва и на­ко­нец четвёртый гном ¼ ока­зав­ше­го­ся у него мо­ло­ка на­ли­ва­ет пер­во­му. Во всех круж­ках вме­сте мо­ло­ка 2 л.

Сколь­ко мо­ло­ка было пер­во­на­чаль­но в круж­ках, если

а) в конце у всех гно­мов мо­ло­ка ока­за­лось по­ров­ну?

б) в конце у всех гно­мов ока­за­лось мо­ло­ка столь­ко, сколь­ко было в на­ча­ле?

10. Петин счет в банке со­дер­жит 500 дол­ла­ров. Банк раз­ре­ша­ет со­вер­шать опе­ра­ции толь­ко двух видов: сни­мать 300 дол­ла­ров или до­бав­лять 198 дол­ла­ров.

а) Какую мак­си­маль­ную сумму Петя может снять со счета, если дру­гих денег у него нет?

б) Какое наи­мень­шее число опе­ра­ций для этого по­тре­бу­ет­ся?

11. Име­ет­ся семь ста­ка­нов с водой: пер­вый ста­кан за­пол­нен водой на­по­ло­ви­ну, вто­рой — на треть, тре­тий — на чет­верть, чет­вер­тый — на одну пятую, пятый — на одну вось­мую, ше­стой — на одну де­вя­тую, и седь­мой — на одну де­ся­тую. Раз­ре­ша­ет­ся пе­ре­ли­вать всю воду из од­но­го ста­ка­на в дру­гой или пе­ре­ли­вать воду из од­но­го ста­ка­на в дру­гой до тех пор, пока он не за­пол­нит­ся до­вер­ху. Может ли после не­сколь­ких пе­ре­ли­ва­ний какой‐ни­будь ста­кан ока­зать­ся за­пол­нен­ным

а) на одну две­на­дца­тую;

б) на одну ше­стую?

12. Ком­пью­тер может про­из­во­дить одну опе­ра­цию: брать сред­нее ариф­ме­ти­че­ское двух целых чисел. Даны три числа: m, n и 0, при­чем m и n не имеют общих де­ли­те­лей и m n До­ка­жи­те, что с по­мо­щью ком­пью­те­ра из них можно по­лу­чить

а) еди­ни­цу;

б) любое целое число от 1 до n.

13. В Мек­си­ке эко­ло­ги до­би­лись при­ня­тия за­ко­на, по ко­то­ро­му каж­дый ав­то­мо­биль хотя бы один день в не­де­лю не дол­жен ез­дить (вла­де­лец со­об­ща­ет по­ли­ции номер ав­то­мо­би­ля и «вы­ход­ной» день не­де­ли этого ав­то­мо­би­ля). В не­ко­то­рой семье все взрос­лые же­ла­ют ез­дить еже­днев­но (каж­дый — по своим делам!). Сколь­ко ав­то­мо­би­лей (как ми­ни­мум) долж­но быть в семье, если взрос­лых в ней

а) 5 че­ло­век?

б) 8 че­ло­век?

14. Два шах­ма­ти­ста иг­ра­ют между собой в шах­ма­ты с ча­са­ми (сде­лав ход, шах­ма­тист оста­нав­ли­ва­ет свои часы и пус­ка­ет часы дру­го­го). Из­вест­но, что после того, как оба сде­ла­ли по 40 ходов, часы обоих шах­ма­ти­стов по­ка­зы­ва­ли одно и то же время: 2 часа 30 мин.

а) До­ка­жи­те, что в ходе пар­тии был мо­мент, когда часы од­но­го об­го­ня­ли часы дру­го­го не менее, чем на 1 мин. 51 сек.

б) Можно ли утвер­ждать, что в не­ко­то­рый мо­мент раз­ни­ца по­ка­за­ний часов была равна 2 мин.?

15. У Лены три на­бо­ра, в каж­дом из ко­то­рых оди­на­ко­вое ко­ли­че­ство ручек (боль­ше 1). У Юли не­сколь­ко (боль­ше 1) на­бо­ров ручек, по 5 штук в каж­дом.

а) При каком ко­ли­че­стве на­бо­ров у Юли, ко­ли­че­ство всех ручек у Лены не­чет­но, если всего у де­во­чек 105 ручек?

б) Можно ли раз­ло­жить все ручки Юли и Лены в 12 на­бо­ров по 12 ручек в кждом?

в) Можно ли раз­ло­жить все ручки Юли и Лены в k на­бо­ров по k ручек в каж­дом (k 3)?

16. Луж­ков и Ба­ту­ри­на по­во­ра­чи­ва­ют с Руб­лев­ки на МКАД в раз­ные сто­ро­ны — Луж­ков — на­ле­во, Ба­ту­ри­на — на­пра­во. За сколь­ко минут каж­дый из них про­ез­жа­ет пол­ный круг по МКАД, если из­вест­но, что Луж­ков тра­тит на 12 минут мень­ше Ба­ту­ри­ной, при этом про­ез­жая круг не быст­рее 31 ми­ну­ты. Время про­ез­да од­но­го круга из­ме­ря­ет­ся целым чис­лом минут и их седь­мая встре­ча про­изо­шла снова на Рублёвке.

17. Гу­бер­на­тор Тить­кин решил ор­га­ни­зо­вать ав­то­бус­ное дви­же­ние между де­рев­ня­ми Верх­нее и Ниж­нее Га­дю­ки­но. Ав­то­бу­сы‐экс­прес­сы будут сле­до­вать из Ниж­не­го Га­дю­ки­но в Верх­нее без оста­но­вок круг­ло­су­точ­но с ин­тер­ва­лом ровно 7 минут, оста­нав­ли­вать­ся в ко­неч­ном пунк­те на какое‐то время и от­прав­лять­ся об­рат­но, тратя на до­ро­гу в одну сто­ро­ну ровно 25 минут. При этом на ко­неч­ных оста­нов­ках не долж­но на­хо­дить­ся более од­но­го ав­то­бу­са од­но­вре­мен­но. Сколь­ко ав­то­бу­сов по­тре­бу­ет­ся ку­пить гу­бер­на­то­ру?

18. а) На по­сто­я­лом дворе оста­но­вил­ся пу­те­ше­ствен­ник, и хо­зя­ин со­гла­сил­ся в ка­че­стве упла­ты за про­жи­ва­ние брать коль­ца зо­ло­той це­поч­ки, ко­то­рую тот носил на руке. Но при этом он по­ста­вил усло­вие, чтобы опла­та была еже­днев­ной: каж­дый день хо­зя­ин дол­жен был иметь на одно коль­цо боль­ше, чем в преды­ду­щий. За­мкну­тая в коль­цо це­поч­ка со­дер­жа­ла 11 колец, а пу­те­ше­ствен­ник со­би­рал­ся про­жить ровно 11 дней, по­это­му он со­гла­сил­ся. Какое наи­мень­шее число колец он дол­жен рас­пи­лить, чтобы иметь воз­мож­ность пла­тить хо­зя­и­ну?

б) Из сколь­ких колец долж­на со­сто­ять це­поч­ка, чтобы пу­те­ше­ствен­ник мог про­жить на по­сто­я­лом дворе наи­боль­шее число дней при усло­вии, что он может рас­пи­лить толь­ко n колец?

19. Тре­бу­ет­ся сде­лать набор гирек, каж­дая из ко­то­рых весит целое число грам­мов, с по­мо­щью ко­то­рых можно взве­сить любой целый вес от 1 грам­ма до 55 грам­мов вклю­чи­тель­но даже в том слу­чае, если не­ко­то­рые гирь­ки по­те­ря­ны (гирь­ки кла­дут­ся на одну чашку весов, из­ме­ря­е­мый вес — на дру­гую).

а) не­об­хо­ди­мо по­до­брать 10 гирек, из ко­то­рых может быть по­те­ря­на любая одна;

б) не­об­хо­ди­мо по­до­брать 12 гирек, из ко­то­рых могут быть по­те­ря­ны любые две. (В обоих слу­ча­ях до­ка­жи­те, что най­ден­ный Вами набор гирек об­ла­да­ет тре­бу­е­мы­ми свой­ства­ми.)

20. Ав­то­бус­ные би­ле­ты имеют но­ме­ра от 000000 до 999999. Билет на­зы­ва­ет­ся счаст­ли­вым, если сумма пер­вых трех цифр его но­ме­ра равна сумме по­след­них трех его цифр. До­ка­жи­те, что:

а) число всех счаст­ли­вых би­ле­тов четно;

б) сумма но­ме­ров всех счаст­ли­вых би­ле­тов де­лит­ся на 999.

21. Ска­жем, что ко­ло­да из 52 карт сло­же­на пра­виль­но, если любая пара ле­жа­щих рядом карт сов­па­да­ет по масти или по до­сто­ин­ству, то же верно для верх­ней и ниж­ней карты, и на­вер­ху лежит туз пик. До­ка­жи­те, что число спо­со­бов сло­жить ко­ло­ду пра­виль­но

а) де­лит­ся на 12!;

б) де­лит­ся на 13!.

22.Груп­па пси­хо­ло­гов раз­ра­бо­та­ла тест, прой­дя ко­то­рый, каж­дый че­ло­век по­лу­ча­ет оцен­ку — число Q — по­ка­за­тель его ум­ствен­ных спо­соб­но­стей (чем боль­ше Q, тем боль­ше спо­соб­но­сти). За рей­тинг стра­ны при­ни­ма­ет­ся сред­нее ариф­ме­ти­че­ское зна­че­ний Q всех жи­те­лей стра­ны.

а) Груп­па граж­дан стра­ны A эми­гри­ро­ва­ла в стра­ну B. Мог ли при этом у обеих стран вы­рас­ти рей­тинг?

б) После этого груп­па граж­дан стра­ны B (в числе ко­то­рых могут быть и быв­шие эми­гран­ты из A) эми­гри­ро­ва­ла в стра­ну A. Воз­мож­но ли, что рей­тин­ги обеих стран опять вы­рос­ли?

в) Груп­па граж­дан стра­ны A эми­гри­ро­ва­ла в стра­ну B, а груп­па граж­дан B — в стра­ну C. В ре­зуль­та­те рей­тин­ги каж­дой стра­ны ока­за­лись выше пер­во­на­чаль­ных. После этого на­прав­ле­ние ми­гра­ци­он­ных по­то­ков из­ме­ни­лось на про­ти­во­по­лож­ное – часть жи­те­лей C пе­ре­еха­ла в B, а часть жи­те­лей B – в A. Ока­за­лось, что в ре­зуль­та­те рей­тин­ги всех стран опять вы­рос­ли (по срав­не­нию с теми, что были после пер­во­го пе­ре­ез­да, но до на­ча­ла вто­ро­го). Может ли такое быть (если да, то как, если нет, то по­че­му)? Пред­по­ла­га­ет­ся, что за рас­смат­ри­ва­е­мое время Q граж­дан не из­ме­ни­лось, никто не умер и не ро­дил­ся.

23. В школе, где учат­ся Поля, Маня и Дуня, есть длин­ный ко­ри­дор вдоль одной из стен ко­то­ро­го рас­по­ло­жен длин­ный ряд из n ячеек, за­ну­ме­ро­ван­ных на­ту­раль­ны­ми чис­ла­ми от 1 до n, за­кры­ва­ю­щих­ся на замки, в ко­то­рых школь­ни­ки могут хра­нить свои лич­ные вещи. Од­на­ж­ды, придя в школу в вы­ход­ной день, Поля об­на­ру­жи­ла все ячей­ки от­кры­ты­ми. Она стала об­хо­дить ряд ячеек сна­ча­ла до конца, за­кры­вая на замок каж­дую вто­рую ячей­ку. До­стиг­нув конца ряда, она раз­вер­ну­лась и снова стала за­кры­вать на замок каж­дую вто­рую ячей­ку из тех, ко­то­рые еще были от­кры­ты. Таким об­ра­зом Поля про­дол­жа­ла об­хо­дить ряд и за­кры­вать на замок ячей­ки до тех пор, пока оста­лась не­за­кры­той одна ячей­ка.

Обо­зна­чим 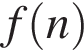номер по­след­ней от­кры­той ячей­ки. На­при­мер, если ко­ли­че­ство ячеек 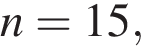то 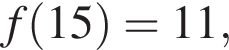как по­ка­за­но на ри­сун­ке

а) Най­ди­те

До­ка­жи­те, что:

б) не су­ще­ству­ет на­ту­раль­но­го числа 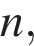та­ко­го что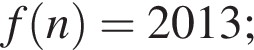

в) су­ще­ству­ет бес­ко­неч­ное мно­же­ство на­ту­раль­ных чисел 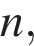таких что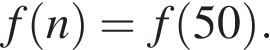

24. Дайте обос­но­ван­ные от­ве­ты на сле­ду­ю­щие во­про­сы.

а) В мешке на­хо­дят­ся 1 жел­тый, 1 зе­ле­ный и 2 крас­ных шара. Из мешка слу­чай­ным об­ра­зом вы­ни­ма­ют 2 шара раз­но­го цвета и за­ме­ня­ют одним шаром тре­тье­го цвета. Этот про­цесс про­дол­жа­ют до тех пор, пока все остав­ши­е­ся шары в мешке не ока­жут­ся од­но­го цвета (воз­мож­но, что при этом в мешке оста­нет­ся один шар) Ка­ко­го цвета шары (или шар) могут остать­ся в мешке?

б) В мешке 3 жел­тых, 4 зе­ле­ных и 5 крас­ных шаров. Ка­ко­го цвета шары (или шар) могут остать­ся в мешке в конце после при­ме­не­ния опи­сан­ной в преды­ду­щем пунк­те про­це­ду­ры?

в) В мешке на­хо­дят­ся 3 жел­тых, 4 зе­ле­ных и 5 крас­ных шаров. Из мешка слу­чай­ным об­ра­зом вы­ни­ма­ют 2 шара раз­но­го цвета и за­ме­ня­ют двумя ша­ра­ми тре­тье­го цвета. Можно ли, при­ме­няя эту про­це­ду­ру мно­го­крат­но, до­бить­ся того, чтобы в мешке ока­за­лись шары од­но­го цвета? Если можно, то ка­ко­го цвета эти шары?

25. У Кости была кучка из 100 ка­меш­ков. Каж­дым ходом он делил какую-то из кучек на две мень­ших, пока у него не ока­за­лось 100 кучек по од­но­му ка­меш­ку.

а) воз­мож­но ли, что в какой-то мо­мент в каких-то 30 куч­ках было ровно 60 ка­меш­ков;

б) воз­мож­но ли, что в какой-то мо­мент в каких-то 20 куч­ках было в сумме ровно 60 ка­меш­ков;

в) мог ли Костя дей­ство­вать так, чтобы ни в какой мо­мент не на­шлось 19 кучек, в ко­то­рых в сумме ровно 60 ка­меш­ков?

26. Рас­смат­ри­ва­ет­ся набор гирь, каж­дая из ко­то­рых весит целое число грам­мов, а общий вес всех гирь равен 500 грам­мов. Такой набор на­зы­ва­ет­ся пра­виль­ным, если любое тело, име­ю­щее вес, вы­ра­жен­ный целым чис­лом грам­мов от 1 до 500, может быть урав­но­ве­ше­но не­ко­то­рым ко­ли­че­ством гирь на­бо­ра, и при­том един­ствен­ным об­ра­зом (тело кла­дет­ся на одну чашу весов, гири – на дру­гую; два спо­со­ба урав­но­ве­ши­ва­ния, раз­ли­ча­ю­щи­е­ся лишь за­ме­ной не­ко­то­рых гирь на дру­гие того же веса, счи­та­ют­ся оди­на­ко­вы­ми).

а) При­ве­ди­те при­мер пра­виль­но­го на­бо­ра, в ко­то­ром не все гири по од­но­му грам­му.

б) Сколь­ко су­ще­ству­ет раз­лич­ных пра­виль­ных на­бо­ров?

(Два на­бо­ра раз­лич­ны, если не­ко­то­рая гиря участ­ву­ет в этих на­бо­рах не оди­на­ко­вое число раз.)

27. а) В клас­се была дана кон­троль­ная. Из­вест­но, что по край­ней мере две трети задач этой кон­троль­ной ока­за­лись труд­ны­ми: каж­дую такую за­да­чу не ре­ши­ли по край­ней мере две трети школь­ни­ков. Из­вест­но также, что по край­ней мере две трети школь­ни­ков клас­са на­пи­са­ли кон­троль­ную хо­ро­шо: каж­дый такой школь­ник решил по край­ней мере две трети задач кон­троль­ной. Могло ли такое быть?

б) Из­ме­нит­ся ли ответ в этой за­да­че, если за­ме­нить везде в ее усло­вии две трети на три чет­вер­ти?

в) Из­ме­нит­ся ли ответ в этой за­да­че, если за­ме­нить везде в ее усло­вии две трети на семь де­вя­тых?

28. Бан­ко­мат об­ме­ни­ва­ет мо­не­ты: дуб­ло­ны на пи­сто­ли и на­о­бо­рот. Пи­столь стоит s дуб­ло­нов, а дуб­лон — 1/s пи­сто­лей, где s — не обя­за­тель­но целое. В бан­ко­мат можно вбро­сить любое число монет од­но­го вида, после чего он вы­да­ет в обмен мо­не­ты дру­го­го вида, округ­ляя ре­зуль­тат до бли­жай­ше­го це­ло­го числа (если бли­жай­ших чисел два, вы­би­ра­ет­ся боль­шее).

а) Может ли так быть, что об­ме­няв сколь­ко-то дуб­ло­нов на пи­сто­ли, а затем об­ме­няв по­лу­чен­ные пи­сто­ли на дуб­ло­ны, мы по­лу­чим боль­ше дуб­ло­нов, чем было в на­ча­ле?

б) Если да, то может ли слу­чит­ся, что по­лу­чен­ное число дуб­ло­нов еще уве­ли­чит­ся, если про­де­лать с ними такую же опе­ра­цию?

29. Гео­ло­ги взяли в экс­пе­ди­цию 80 банок кон­сер­вов, веса ко­то­рых все из­вест­ны и раз­лич­ны (име­ет­ся спи­сок). Через не­ко­то­рое время над­пи­си на бан­ках стали не­чи­та­е­мы­ми, и толь­ко зав­хоз знает где что. Он может все это до­ка­зать (т. е. обос­но­вать, что в какой банке на­хо­дит­ся), не вскры­вая кон­сер­вов и поль­зу­ясь толь­ко со­хра­нив­шим­ся спис­ком и двух­ча­шеч­ны­ми ве­са­ми со стрел­кой, по­ка­зы­ва­ю­щей раз­ни­цу весов на чаш­ках. До­ка­жи­те, что ему для этой цели

а) до­ста­точ­но че­ты­рех взве­ши­ва­ний;

б) не­до­ста­точ­но трех взве­ши­ва­ний.

Ком­мен­та­рий. От­ме­тим еще раз, что зав­хоз дол­жен обос­но­вать, что в какой банке на­хо­дит­ся для всех 80 банок.

30. Среди любых де­ся­ти из ше­сти­де­ся­ти школь­ни­ков най­дет­ся три од­но­класс­ни­ка. Обя­за­тель­но ли среди всех ше­сти­де­ся­ти школь­ни­ков най­дет­ся

а) 15 од­но­класс­ни­ков;

б) 16 од­но­класс­ни­ков?

31. Трид­цать три бо­га­ты­ря на­ня­лись охра­нять Лу­ко­мо­рье за 240 монет. Хит­рый дядь­ка Чер­но­мор может раз­де­лить бо­га­ты­рей на от­ря­ды про­из­воль­ной чис­лен­но­сти (или за­пи­сать всех в один отряд), а затем рас­пре­де­лить все жа­ло­ва­ние между от­ря­да­ми. Каж­дый отряд делит свои мо­не­ты по­ров­ну, а оста­ток от­да­ет Чер­но­мо­ру. Какое наи­боль­шее ко­ли­че­ство монет может до­стать­ся Чер­но­мо­ру, если:

а) жа­ло­ва­ние между от­ря­да­ми Чер­но­мор рас­пре­де­ля­ет как ему угод­но;

б) жа­ло­ва­ние между от­ря­да­ми Чер­но­мор рас­пре­де­ля­ет по­ров­ну?

32. На шести елках сидят шесть сорок — по одной на каж­дой елке. Елки рас­тут с ин­тер­ва­лом в 10 м. Если какая-то со­ро­ка пе­ре­ле­та­ет с одной елки на дру­гую, то какая-ни­будь, дру­гая со­ро­ка обя­за­тель­но пе­ре­ле­та­ет на столь­ко же мет­ров, но в об­рат­ном на­прав­ле­нии.

а) Могут ли все со­ро­ки со­брать­ся на одной елке?

б) А если сорок и елок семь?

в) А если елки стоят по кругу?

33. Име­ют­ся ка­мен­ные глыбы: 50 штук по 800 кг, 60 штук по 1000 кг и 60 штук по 1500 кг (рас­ка­лы­вать глыбы нель­зя).

а) Можно ли увез­ти все эти глыбы од­но­вре­мен­но на 60 гру­зо­ви­ках, гру­зо­подъ­ем­но­стью 5 тонн каж­дый, пред­по­ла­гая, что в гру­зо­вик вы­бран­ные глыбы по­ме­стят­ся?

б) Можно ли увез­ти все эти глыбы од­но­вре­мен­но на 38 гру­зо­ви­ках, гру­зо­подъ­ем­но­стью 5 тонн каж­дый, пред­по­ла­гая, что в гру­зо­вик вы­бран­ные глыбы по­ме­стят­ся?

в) Какое наи­мень­шее ко­ли­че­ство гру­зо­ви­ков, гру­зо­подъ­ем­но­стью 5 тонн каж­дый, по­на­до­бит­ся, чтобы вы­вез­ти все эти глыбы од­но­вре­мен­но, пред­по­ла­гая, что в гру­зо­вик вы­бран­ные глыбы по­ме­стят­ся?