Составитель: Дюйсенова К.Ж.
Вашему вниманию предлагается система карточек для коррекции знаний по курсу математики 5-6 классов.
Карточки охватывают ключевые вопросы курса. Каждая посвящается одному отдельному вопросу и состоит из трех частей: инструкции (формулировки правила), образца применения этой инструкции и пятнадцати заданий для обучающихся.
Карточки предназначены для дополнительных занятий с обучающимися (в классе или дома). Если ученик на таком занятии правильно выполнил первые пять заданий из пятнадцати, этого достаточно. Если же он не смог этого сделать, то учитель должен объяснить ему материал и дать следующие пять заданий. Если и эти задания обучающийся не может выполнить, объяснение продолжается, и решаются остальные пять заданий.
Карточка №1. Сложение и вычитание многозначных чисел (повторение)
| Правило | Образцы | Задания |
| Складывай и вычитай числа по одноименным разрядам | 2537+42768=? | Десятки тысяч | тысячи | сотни | десятки | единицы | | +
2 | 5 | 3 | 7 |
| | 4 | 2 | 7 | 6 | 8 | | 4 | 5 | 3 | 0 | 5 |
+ 2537 42768 45305
42567-3786=? | Десятки тысяч | тысячи | сотни | десятки | единицы | | - 4 2 | 5 | 6 | 7 |
| |
| 3 | 7 | 8 | 6 | | 3 | 8 | 7 | 8 | 1 |
_42567 _3786 38781
| Найти суммы и разности: |
| 3721+12354 72046-6458 24237+13142 690859-74860 2717+1021 |
| 32210+4372 89194-11225 6246+1737 799298-672709 43160+28328 |
| 1533+1025 14572-6595 832725+743132 726136-483678 145993+777428 |
Карточка №2. Умножение столбиком (повторение)
| Правило | Образцы | Задания |
| Выполняй задания по образцам | ₓ707 2) ₓ104 216 205 4242 + 520 + 707 208___ 1414___ 21320 152712
3) ₓ30100 1052 602 + 1505 301____ 4575200
| Найти произведения: |
| 240•517 206•137 1163•105 1100•740 6001•107 |
| 864•285 601•312 102•3012 1309•610 1023•600 |
| 610•281 204•112 1264•500 2301•160 1025•308
|
Карточка №3. Деление углом (повторение)
| Правило | Образцы | Задания |
| Выполняй задание по образцу | _19034│_62__ 186_ 307 _434 434 0 | Найти частные: |
| 215:5 6210:6 1944:36 52800:165 35926:142 |
| 2431:11 12960:12 23856:112 27404:34 21632:104 |
| 13617:17 199076:628 1425680:5020 400911:1123 726172:362
|
Карточка №4. Сравнение десятичных дробей
| Правило | Образцы | Задания |
| да нет    Целые части равны? нет

Больше та дробь, у которой она больше
да 

Цифры десятых равны  Цифры сотых равны нет 
| 1) 12,86 и 18,06 12 2) 6,453 и 6,2883 6=6 42→6,4536,2883 3) 120,3586 и 120,36 120=120 3=3 5 4) 2,112 и 2,1100 2=2 1=1 1=1 20→2,1122,1100 | Сравнить дроби: |
| 1,24 и 2,3 6,001 и 1,08 19,78 и 11,02 5,001 и 4,2 32,11 и 28,10 |
| 0,34 и 0,28 2,4 и 2,50 1,7 и 1, 68 21,57 и 21,6 1,405 и 1,726 |
| 0,34 и 0,38 1,024 и 1,014 4,014 и 4,02 5,16 и 5,1388 49,1803 и 49,18
|
Карточка №5. Сложение и вычитание десятичных дробей (повторение)
| Правило | Образцы | Задания |
| Складывай и вычитай числа по одноименным разрядам | 4,608-0,2067=? | единицы |
| десятые | сотые | тысячные | десятичные | | - 4 , | 6 | 0 | 8 | 0 |
| | 0 | , | 2 | 0 | 6 | 7 | | 4 | , | 4 | 0 | 1 | 3 |
_4,6080 0,2067 4,4013
| Вычислить: |
| 8,3+6,2 2,43-1,3 3,5+1,74 5-2,71 7,203-1,1025 |
| 3,13+7,25 7,23-2,104 13,430+1,442 16,456-2,721 1,400-17,108 |
| 2,40+5,38 12,211-9,30 10,511+10,283 174,763-2,85 43,174-33,015
|
Карточка №6. Умножение десятичных дробей
| Правило | Образцы | Задания |
Зачеркни имеющиеся запятые. Перемножь получившиеся натуральные числа. Отдели в произведении столько десятичных знаков, сколько их во всех сомножителях вместе. | 0,14•1,3•2=? 1) 0,14→14 1,3→13 2→2 14•13•2=364 364→0,364 Ответ: 0,14•1,3•2=0,364 Краткая запись: 0,14•1,3•2=0,364 2+1+0=3 | Найти произведения: |
| 0,3•5,6 18,6•0,1 6,3•0,03 0,04•0,11 3,2•5 |
| 4,7•0,2 0,03•0,5 35,1•0,01 0,006•0,04 1,02•0,3 |
| 1,7•0,5 0,06•0,2 1,62•0,001 2,35•3 0,023•0,05
|
Карточка №7. Деление десятичной дроби на натуральное число.
| Правило | Образцы | Задания |
| Дели дробь как целое число. Сразу после снесения цифры десятых поставь запятую в частном и продолжай деление. | _2452,800│75 225 32,704 _202 150 _528 525 _300 300 0 | Найти частные: |
| 6,3:3 16,4:4 1711,8:6 4,8:8 3,675:7 |
| 72,0:16 28,084:14 0,63:15 1:25 |
| 27,54:27 130,052:26 1303,9:13 0,036:12 6:15
|
Карточка №8. Вычисление значений буквенных выражений.
| Правило | Образцы | Задания |
Подставь численные значения переменных вместо букв. Найди значение получившегося числового выражения. | Найти значение выражения: a+7-(b+6) если a=25, b=13 Решение: a+7-(b+6)=25+7-(13+6)=32-19=13 | Найти значения выражений: |
| a + 3, если a=7 50-x, если x=23 4y, если y=15 a+b, если a=8, b=5 m:n, если m=12, n=4 |
| 3+b, если b=14 k-37, если k=88 11a, если a=6 n-m,если m=7, n=43 ac, если a=12, c=4 |
| f-39, если f=77 t+13,если t=28 16d,если d=3 p-q, если p=4, q=9 y:x, если x=5, y=25
|
Карточка №9. Решение простейших уравнений.
| Правило | Образцы | Задания |
| Найди похожий образец и выполни задания. | х+13=19 2) х-3=9 х=19-13 х=9+3 х=6 х=12
3) 29-х=18 4) х•7=35 х=29-18 х=35:7 х=11 х=5
5) х:4=9 6) 66:х=6 х=9•4 х=66:6 х=36 х=11
| х+634=1876 х-2713=3425 684-х=437 57•y=11571 х:302=27 |
| 5204+y=8415 х-1232=807 1025-х=963 х•212=3180 6880:х=215 |
| х+675=2125 х-769=3174 243•х=10935 х:32=175 189:х=27
|
Карточка №10. Нахождение процентов от числа.
| Правило | Образцы | Задания |
Напиши, что 100%-это a. Найди 1% от a. Найди х% от a. | Найди 2% от 2000м. Решение: 100%-это 2000м 1%-это 2000:100 1%-это 20 2%-это 20•2 2%-это 40м Ответ: 40м Краткая запись: (2000:100)•2=2000•2 =40 100
| Найди 2% от 600. Найди 15% от 6. Найди 6% от 3 кг. Прибор стоимостью 4000 тнг подешевел на 20%. На сколько тнг подешевел прибор? Что больше, 40% от 20 или 30% от 40? |
| Найди 4% от 1600. Найди 13% от 5. Найди 8% от 7 км. В городе было 3млн жителей. За 10 лет население выросло на 17%. Сколько теперь жителей в городе? Что больше 41% от 57 или 57% от 41? |
| Найди 5% от 2100. Найди 18% от 2. Найди 8% от 1 ч. Вклад в 2000$ за год увеличился на 5%. Чему теперь равен вклад? Что больше 50% от 47 или 52% от 49? |
Карточка №11. Нахождение процентного отношения.
| Правило | Образцы | Задания |
Напиши, что 100% - это b. Найди 1% от b. Найди сколько раз 1% от b помещается в a.
| Найди процентное отношение числа 7 к числу 2,5. Решение: 100% - это 2,5 1% - это 2,5•100 1% - это 0,025 0,025 помещается в числе 7. 7:0,025=280 раз. Ответ: 280. Краткая запись: 7:(2,5:100)=7•100 =280 2,5
| Найди процентное отношение: а) 2 к 100 б) 13 к 6,5 Сколько процентов составляет: а) 17 от 50? б) 2,8 от 350? Если в твоем классе 25 учеников, то сколько процентов класса составляешь ты? |
| Найди процентное отношение: а) 12 к 50 б) 19 к 9,5 Сколько процентов составляет: а) 23 от 200 б) 3,8 от 5,7 Полстакана чая долили молоком 6% жирности. Каков процент жира в чае? |
| Найди процентное отношение: а) 29 к 25 б) 14 к 9,1 Сколько процентов составляет: а) 17 от 50 б) 2,8 от 5,6 В классе 12 девочек и 16 мальчиков. Найти процентное отношение этих чисел.
|
Карточка №12. Нахождение числа по его процентам.
| Правило | Образцы | Задания |
Напиши, что n % числа равны a. Найди 1% числа. Найди 100% (само число). | Найди число 3% которого равны 960. Решение: 3% - это 960 1% - это 960:3 1% - это 320 100% - это 320•100 100% - это 32000 Ответ: 32000 Краткая запись: (960:3)•100=960•100 = 32000 3 | 6% какого числа равны 180? 16% какого числа равны 36? Найти стоимость товара, 14% которой равны 3500 тнг. Найти расстояние, 73% которого равны 2,6 км. 20% вклада в сбербанк составляют 8000 тнг. Чему равен весь вклад? |
| 5% какого числа равны 30. 15% какого числа равны 21. Найти стоимость товара, 13% которой равны 6500 тнг. Найти площадь, 26% которой равны 5,2 см. 20% вклада в сбербанк составляют 8000 тнг. Чему равен весь вклад? |
| 10% какого числа равны 240. 13% какого числа равны 39. Найти стоимость товара, 15% которого 2250 тнг. Найти расстояние, 87% которого равны 17,4 км. 30% вклада в сбербанк составляют 45000 тнг. Чему равен весь вклад?
|
Карточка №13. Сравнение, сложение и вычитание дробей с одинаковыми знаменателями.
| Правило | Образцы | Задания |
| Сравнивай, складывай или вычитай числители. | + - = = = = 4 2 , так как 42. 5 5
4 2 4+2 6 5 5 5 5 4 2 4-2 2 5 5 5 5
| Сравнить дроби, найти их суммы и разности: 11 и 9 ; 7 и 9 ; 17 и 15 20 20 15 15 19 19
3 и 5 ; 14 и 4 7 7 11 11 |
| 15 и 11 ; 8 и 29 ; 4 и 17 63 63 33 33 25 25
17 и 15 ; 64 и 13 32 32 9 9
|
| 27 и 29 ; 105 и 215 ; 13 и 27 102 102 156 156 144 144
11 и 7 ; 14 и 26 201 201 11 11
|
Карточка №14. Основное свойство дроби.
| Правило | Образцы | Задания |
| Приведи дробь к новому знаменателю: умножь (или раздели) знаменатель дроби на число. умножь (или раздели) числитель дроби на то же число. | 1) Привести дробь 2 к 3 знаменателю 18. Решение: 3•6=18 2•6=12 Ответ: 12 18
2) Привести дробь 8 к 14 знаменателю 7. Решение: 14:2=7 8:2=4 Ответ: 4 7
| Привести дроби: а) 1 к знаменателю 22; б) 3 к знаменателю 7. 2 21 Разделить числитель и знаменатель дроби 6 20 на 2; умножить числитель и знаменатель дроби 1 на 4. 3 Разделить 26 на 2. 40 |
| Привести дроби: а) 3 к знаменателю 28; б) 12 к знаменателю 7. 4 21 Разделить числитель и знаменатель дроби 36 58 на 2. Умножить числитель и знаменатель дроби 3 на 5. 8 Разделить 42 на 7. 98 |
| Привести дроби: а) 4 к знаменателю 36; б) 33 к знаменателю 11. 9 77 Разделить числитель и знаменатель дроби 28 на 7. 49 Умножить числитель и знаменатель дроби 3 на 4. Разделить 55 на 11. 7 99 |
Карточка №15. Умножение дробей.
| Правило | Образцы | Задания |
| Умножить числитель на числитель, а знаменатель на знаменатель: a . c = ac b d bd
| 1) 3 • 4 = 3•4 = 12 5 7 5•7 35
2) 3 • 4 = 3•4 = 12 1 7 1•7 7
3) 5 • 13 = 5•13 = 13 3 5 3•5 3
| Найти произведения: 1 • 4 ; 4 • 5 ; 4 • 5 ; 4 • 3 ; 3 • 11 3 5 7 9 1 11 3 4 2 5 |
| 7 • 1 ; 8 • 3 ; 4 • 3 ; 7 • 2 ; 7 • 4 9 2 9 7 13 1 3 5 2 3
|
| 4 • 2 ; 7 • 6 ; 7 • 2 ; 6 • 16 ; 11 • 10 7 5 8 5 9 1 11 3 4 9 |
Карточка №16. Деление дробей.
| Правило | Образцы | Задания |
| Умножить числитель на знаменатель, а знаменатель на числитель: a : c = ad b d bc
| 1) 2 : 3 = 2•7 = 14 5 7 5•3 15
2) 3 : 21 = 3•1 = 1 7 1 7•21 49
3) 55 : 11 = 55•7 = 35 1 7 1•11 1
4) 5 : 55 = 5•6 = 2 3 6 3•55 11
5) 9 : 101 = 9•1 = 9 1 1 1•101 101 | Найти частные: 4 : 3 ; 2 : 7 ; 5 : 9 ; 4 : 1 ; 15 : 19 9 5 3 1 1 1 1 8 2 2 |
| 16 : 31 ; 2 : 7 ; 1 : 3 ; 14 : 2 ; 13 : 10 1 1 7 1 5 7 1 7 3 3
|
| 17 : 37 ; 15 : 5 ; 2 : 11 ; 7 : 14 ; 19 : 38 1 1 1 3 11 1 9 81 7 21
|
Карточка №17. Основное свойство пропорции.
| Правило | Образцы | Задания |
Произведение крайних членов пропорции равно произведению ее средних членов. Неизвестный крайний член пропорции равен произведению ее средних членов, деленному на известный крайний. Неизвестный средний член пропорции равен произведению ее крайних членов, деленному на известный средний.
| 1) Проверить пропорцию: 9:3=3:1 Решение: 9•1=9 3•3=9 2) Решить уравнение: а) х:7=18:14 б) 25:75=2:х Решение: а) х=7•18:14=9 б) х=75•2:25=6 3) Решить уравнение: а) 24:х=8:13 б) 6:2=х:70 Решение: а) х=24•13:8=39 б) х=6•70:2=210
| Проверить пропорцию: 1:2=0,2:0,4 Решить уравнения: х:6=8:4 5:2=t:4 1:5=х:25 6:3=18:y |
| Проверить пропорцию: 1,8:2=18:20 Решить уравнения: 2:а = 5 : 5 ; х:12 = 75:15 4 12,4 : х = 5,58 : 0,9
2 : 5 = х : 1 3 9 1 3 |
| Проверить пропорцию: 9 : 3 = 12 : 8 10 5 10 10 Решить уравнения: 12,4 : х = 5,58 : 0,9 4,5 : х = 12,5 : 4 1,5 : 2 = х : 8
3 = 18 1 у |
Карточка №18. Сложение рациональных чисел с помощью координатной прямой.
| Правило | Образцы | Задания |
Чтобы прибавить к числу а положительное число b, достаточно продвинуться от а вправо на b единиц. Чтобы прибавить к числу а отрицательное число b, достаточно продвинуться от а влево на (-b) единиц.
| -2 -7 -3 1    ) (-6)+4=? ) (-6)+4=?     
 -6
Ответ: (-6)+4=-2 2) (-7)+(-3)=?    
Ответ: (-7)+(-3)=-10 | Найти суммы: 4+5 6+(-3) (-2)+7 (-4)+(-5) (-3)+3 |
| 5+6 8+(-4) (-5)+3 4+(-7) 4+(-4) |
| 2+6 7+(-4) -5+7 -3+(-5) 6+(-6)
|
Карточка №19. Сложение рациональных чисел без помощи координатной прямой.
| Правило | Образцы | Задания |
| 
Числа а и в одного знака? |а+в|=|а|+|в| знак тот же |а+в|=|а|-|в| знак числа a     да |а||в| нет
| 1) (-6)+(-2)=? Решение: Числа (-6) и (-2) одного знака, значит: │-6+(-2)│=│-6│+│-2│=8 Знак тот же – минус. Ответ: (-6)+(-2)=-8 2) 4+(-9)=? Решение: Числа 4 и (-9) разных знаков, │-9││4│, значит: │4+(-9)│=│-9│-│4│=5 Значит числа (-9) – минус. Ответ: 4+(-9)=-5
| Найти суммы: |
| 2+4 6+(-3) (-5)+7 (-4)+(-6) (-2)+2 |
| 5+3 8+(-5) (-6)+4 (-3)+(-2) 4+(-4) |
| 4+6 7+(-3) (-4)+5 (-7)+(-6) (-5)+5 |
Карточка №20. Вычитание рациональных чисел.
| Правило | Образцы | Задания |
| а – b = a + (-b) | 1) (-6) - (-2) = (-6) + 2 = -4 2) 5 – 13 = 5 + (-13) = -8 | Найти разности: 2-4 6-(-3) (-5)-7 (-3)-(-4) (-3)-3 |
| 3-7 9-(-4) (-5)-3 -6-(-4) 5-(-5) |
| 4-9 5-(-3) (-2)-7 (-6)-(-4) (-4)-4
|
Карточка №21. Умножение рациональных чисел.
| Правило | Образцы | Задания |
| │a•b│=│a│•│b│ Если a и b одного знака, то знак произведения плюс, а если разных – то минус.
| 1) (-5)•(-2)=? Решение: │(-5)•(-2)│=│-5│•│-2│=5•2=10, (-5) и (-2) одного знака, поэтому знак произведения плюс. Ответ: (-5)•(-2)=10 2) 5•(-2)=? Решение: │5•(-2)│=│5│•│-2│=5•2=10, 5 и (-2) разных знаков, поэтому знак произведения минус. Ответ: 5•(-2)=-10.
| Найти произведения: 6•5 6•(-5) (-6)•5 (-6)•(-5) 0,6•(0,05) |
| 7•8 7•(-8) (-7)•8 (-7)•(-8) (-0,08)•0,7 |
| 9•6 9•(-6) (-9)•6 (-9)•(-6) 0,9•(-0,06)
|
Карточка №22. Деление рациональных чисел.
| Правило | Образцы | Задания |
| │a:b│=│a│:│b│ Если a и b одного знака, то знак частного плюс, а если разных – то минус.
| 1) (-21):(-7)=? Решение: │(-21):(-7)│=│-21│:│-7│=21:7=3, (-21) и (-7) имеют одинаковые знаки, поэтому знак частного плюс. Ответ: (-21):(-7)=3 2) 21:(-7)=? Решение: │21:(-7)│=│21│:│-7│=21:7=3, 21 и (-7) имеют разные знаки, поэтому знак частного минус. Ответ: 21:(-7)=-3 | Найти частные: |
| 35:5 35:(-5) (-35):5 (-35):(-5) (-0,35):(-0,05) |
| 45:9 45:(-9) (-45):9 (-45):(-9) (-0,45):(-0,09) |
| 63:7 63:(-7) (-63):7 (-63):(-7) (-0,63):(-0,07)
|
ММ «Перелески орта мектебі»
ГУ «Перелескинская средняя школа»
МАТЕМАТИКА 5-6 КЛАССЫ
Карточки для коррекции знаний.
2 013 год
013 год
2

 Получите свидетельство
Получите свидетельство Вход
Вход




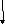


 ) (-6)+4=?
) (-6)+4=? 












 Материал по математике "Карточки для коррекции знаний" (0.23 MB)
Материал по математике "Карточки для коррекции знаний" (0.23 MB)
 0
0 9491
9491 1785
1785 Нравится
0
Нравится
0






