1. В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA = KB. Докажите, что данный параллелограмм — прямоугольник.
2. В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.
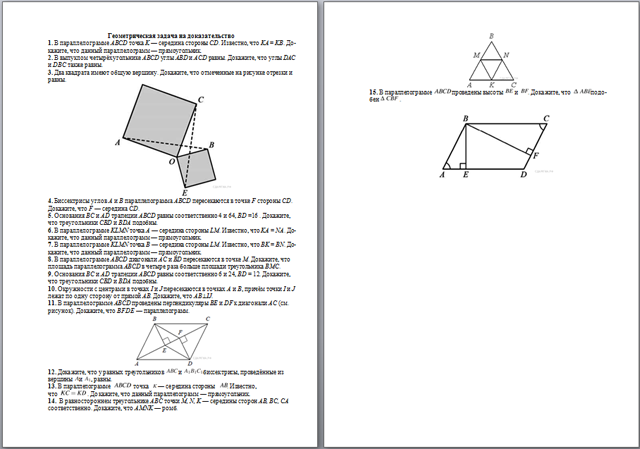
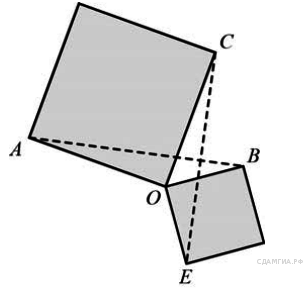
3. Два квадрата имеют общую вершину. Докажите, что отмеченные на рисунке отрезки и равны.
4. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке F стороны CD. Докажите, что F — середина CD.
5. Основания BC и AD трапеции ABCD равны соответственно 4 и 64, BD =16 . Докажите, что треугольники CBD и BDA подобны.
6. В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA = NA. Докажите, что данный параллелограмм — прямоугольник.
7. В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK = BN. Докажите, что данный параллелограмм — прямоугольник.
8. В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BMC.
9. Основания BC и AD трапеции ABCD равны соответственно 6 и 24, BD = 12. Докажите, что треугольники CBD и BDA подобны.
10. Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что AB⊥IJ.
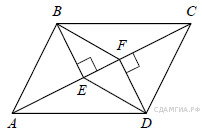
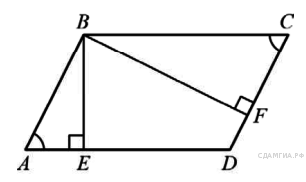
11. В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что ВFDЕ — параллелограмм.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Материал по математике "Геометрическая задача на доказательство" (89.95 КB)
Материал по математике "Геометрическая задача на доказательство" (89.95 КB)
 0
0 954
954 96
96 Нравится
0
Нравится
0


