Материал для учителя математики в 10-11 классе профильной школы. Раздел «Элементы теории вероятностей и математической статистики»
Теорема Байеса на службе прогноза развития современности
Введение
Мы живем в мире общения, поэтому регулярно получаем сообщения, которые влияют на наше восприятие окружающего мира, на наши убеждения. Информативность сообщения определяется уровнем воздействия его на наши убеждения. Но нужно знать, какие были наши убеждения до получения сообщения. Одна и та же информация по-разному меняет убеждения об окружающем мире разных людей, в разных условиях. Тогда мы увидим, насколько поменялись убеждения после получения информации (сообщения)
Информатика, как наука должна учитывать многообразие нашего мира, в том числе различия в опыте и ожиданиях наблюдателей. Информативность сообщения всегда определяется новизной, неожиданностью и важностью. Но надо еще учесть то, что одно и то же сообщение может быть для одного человека более неожиданным, чем для другого. Новым или неожиданным мы можем назвать только то сообщение, которое меняет наши представления об окружающем мире, наше поведение.
Например, вчера я собирался пойти навестить подругу, но получил сообщение, что она уехала. Вместо этого я иду в спортзал. Там я встречаю знакомую. Она никак не прореагировала на сообщение об отъезде моей подруги. Она не знает мою подругу и не ходит к ней.
Решение этой проблемы нашел человек, который является, наверное, самым необычным из всех ученых, почитаемых программистами всего мира.
История знает много примеров того, как труды ученых предавались забвению и не были оценены по достоинству потому, что их открытия не нашли практического применения в условиях того времени. Такая участь постигла и преподобного Байеса.
Том Байес – английский математик и религиозный деятель, член Лондонского королевского общества. Он родился в 1702 году в Лондоне. После основательного домашнего обучения поступил в Эдинбургский университет. Помогал отцу в церковной службе, затем сам стал священником. Увлекался математикой, в частности теорией вероятностей.
Он сформулировал и решил одну из основных задач этого раздела математики (теорему Байеса). Работа, посвящённая этой задаче, была опубликована через 2 года после его смерти, в 1763 году. Формула Байеса, дающая возможность оценить вероятность событий эмпирическим путем, играет важную роль в современной математической статистике и теории вероятностей. Другая крупная его работа — «Очерки к решению проблемы доктрины шансов». Используется терминология: байесовская оценка решения, байесовский подход к статистическим законам, байесианизм и т. п.
Настоящее признание он получил с началом эры компьютерных технологий. В 2002 году разработчики программного обеспечения всего мира отмечали 300-летие со дня рождения этого выдающегося ученого, опередившего свое время.
В настоящее время Байесовские методы получили достаточно широкое распространение и активно используются в самых различных областях знаний. Однако, к сожалению, не так много людей имеют представление о том, что же это такое и зачем это нужно. Одной из причин является отсутствие большого количества литературы на русском языке.
Теорема Байеса (или формула Байеса) — одна из основных теорем элементарной теории вероятностей, которая позволяет определить вероятность какого-либо события при условии, что произошло другое статистически взаимозависимое с ним событие. Другими словами, по формуле Байеса можно более точно пересчитать вероятность, беря в расчет как ранее известную информацию, так и данные новых наблюдений. Формула Байеса может быть выведена из основных аксиом теории вероятностей, в частности из условной вероятности. Особенность теоремы Байеса заключается в том, что для ее практического применения требуется большое количество расчетов, вычислений, поэтому байесовские оценки стали активно использовать только после революции в компьютерных и сетевых технологиях.
Математическая запись теоремы Байеса, ее следствия
Если событие А может произойти только при выполнении одного из событий В1,B2,B3,…Вn, которые образуют полную группу несовместных событий, то вероятность Р(А) вычисляется по формуле полной вероятности.
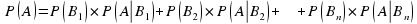
Вновь рассмотрим полную группу несовместных событий В1,B2,B3,…Вn, вероятности появления которых 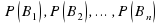 . Событие А может произойти только вместе с каким либо из событий В1,B2,B3,…Вn , которые назовем гипотезами. Тогда по формуле полной вероятности
. Событие А может произойти только вместе с каким либо из событий В1,B2,B3,…Вn , которые назовем гипотезами. Тогда по формуле полной вероятности
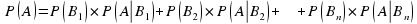
Если событие А произошло, это может изменить вероятности гипотез 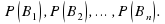
По теореме умножения вероятностей
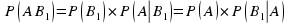
Откуда
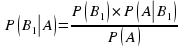
Так же для остальных гипотез:
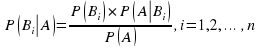
Полученная формула называется формулой Байеса (формулой Бейеса).
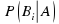 - вероятности гипотез
- вероятности гипотез 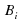 при наступлении события A называются апостериорными вероятностями;
при наступлении события A называются апостериорными вероятностями;
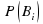 – вероятности гипотез называются априорными вероятностями.
– вероятности гипотез называются априорными вероятностями.
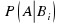 - вероятность наступления события A при истинности гипотезы
- вероятность наступления события A при истинности гипотезы 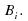
P(А) — вероятность наступления события А.
По формуле Байеса можно более точно пересчитывать вероятность, принимая во внимание как ранее известную информацию (априорные данные), так и данные новых наблюдений (апостериорные данные).
Следствием формулы Байеса является формула полной вероятности события, зависящего от нескольких несовместных гипотез. Запишем ее используя оператор суммы.
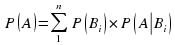
Чтобы использовать эту формулу, мы должны знать заранее достоверности гипотез (например, установить это с помощью наблюдений, экспериментов). Тогда с помощью следствия из теоремы Байеса мы можем определить вероятность события A, зависящего от этих гипотез.
Мы каждый день сталкиваемся с Байесовскими идеями. Достоверность событий определяем с учетом определенных условий, опыта. Просто мы не формулируя накапливаем определенную статистику, которая позволяет нам с определенной уверенностью (вероятностью) ожидать те или иные события. Просто мы не используем формулы, не просчитываем вероятность в цифрах, а называем все это жизненным или профессиональным опытом. По сути дела, Байес сумел формализовать наши ожидания. Поэтому, чтобы принять определенное решение, не обязательно копить опыт, можно просчитать вероятность, зная условия происхождения события.
Теорему Байеса можно проиллюстрировать таким примером. Кассир некоторого фаст - фуда принимает заказ в условиях шума, поэтому информация искажается. Он может заказ на блюдо А принять за заказ на блюдо В. Блюда А и В пользуются разным спросом у посетителей: Р(А) – вероятность заказа блюда А (рассчитан на основе статистики заказов), Р(B|A) – вероятность ошибки В для данного А. Вероятность правильно услышать клиента правильно равна Р(A|B). Вероятности Р(В) и Р(B|A) являются априорными данными.
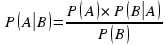
Итак, формулу Байеса пояснили, покажем применение при решении разных типов задач.
Примеры решения задач с использованием формулы Байеса Задача1.
Магазин получает однотипные столы из трех филиалов мебельной фабрики. Из второго филиала поступает столов в 3 раза больше, чем с первого, с третьего филиала – вдвое больше, чем с первого. Вероятность брака в первом филиале 1%, во втором -2% и в третьем 3%. Все изделия хранятся на складе. Покупателю доставляется наудачу выбранный стол со склада. Какова вероятность, что доставлен бракованный стол?
Решение:
Обозначим события поставок с филиалов -А1, А2, А3. Это полная группа. Всего долей 1+2+3=6
А1 P(А1)=1/6
А2 P(А2)=3/6=1/2
А3 P(А3)=2/6=1/3
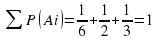
F-бракованный стол.
Условные вероятности:
PA1(F)=0,01 PA2(F)=0,02 PA3(F)=0,03
По формуле полной вероятности:
P (F)= P(А1*F)+ P(А2*F)+ P(А3*F)= P(А1)* PA1(F)+ P(А2)* PA2(F)+ P(А3)* PA3(F)= 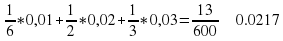
Пусть оказалось так, что покупателю был доставлен бракованный стол. Какова вероятность, что стол изготовлен на 1 филиале? Если известно, что стол бракованный, в каком филиале вероятнее всего был изготовлен?
Ответ получим через переоценку гипотез при дополнении информации по формуле Байеса:
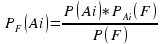
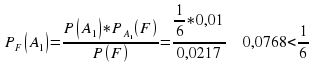
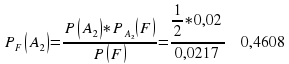
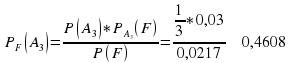
С равной вероятностью стол изготовлен во 2 или 3 филиалах. Маловероятно, что бракованный стол поступил из 1 филиала.
Задача2.
Всего тренировались 20 человек стрелков. Вероятность попадания в цель 10 из них – 0,6, шестеро попадают с вероятностью 0,5, и только четверо имеют вероятность попадания 0,7. Наудачу выбранный стрелок поразил цель. К какой группе вероятнее всего принадлежит стрелок?
Решение: Введем полную группу гипотез:
E1 = (Стрелок из первой группы)
E2 = (Стрелок из второй группы)
E3 = (Стрелок из третьей группы)
Р(E1)=10/20=0,5 Р(E2)=8/20=0,4 Р(E3)=2/20=0,1
Событие F- стрелок попал в мишень.
Условные вероятности:
PЕ1(F)=0,6 PЕ2(F)=0,5 PЕ3(F)=0,7
Найдем вероятность события F По формуле полной вероятности:
P (F)= P(Е1*F)+ P(Е2*F)+ P(Е3*F)= P(Е1)* PЕ1(F)+ P(Е2)* PЕ2(F)+ P(Е3)* PЕ3(F)=
=0,5*0,6+0,4*0,5+0,1*0,7=0,57
Теперь найдем апостериорные вероятности, что попал стрелок группы i.
Используем формулу Байеса.
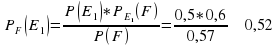
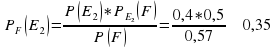
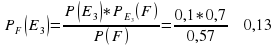
Таким образом, стрелок вероятнее всего принадлежит первой группе.
Ответ: Первая группа.
Задача 3.
В группе 10 студентов, пришедших на экзамен. Трое подготовлены отлично, 4-хорошо, 2-посредственно, 1- плохо. В экзаменационных билетах имеется 20 вопросов. Отлично подготовленный студент может ответить на все 20 вопросов, хорошо подготовленный –на 16, посредственно – на 10, плохо подготовленный – на 5. Вызванный наугад студент ответил на все 3 заданных вопроса. Найти вероятность того, что этот студент подготовлен: 1) отлично 2) хорошо.
Решение: Рассмотрим полную группу событий: A - студент ответит на все вопросы B1 - подготовлен отлично, B2 - подготовлен хорошо, B3 - подготовлен посредственно, B4 - подготовлен плохо.
Вероятности этих событий равны: Р(B1)=0,3; Р(B2)=0,4; Р(B1)=0,2; Р(B1)=0,1 . Найдем условные вероятности: PB1(A)=1; PB2(A)=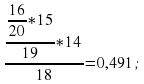 PB3(A)=
PB3(A)=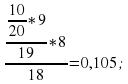 PB4(A)=
PB4(A)=
P(A)=0.3•1+0.491•0.4+0.105•0.2+0.009•0.1=0.518
По формуле Байеса найдем: РA(B1)= =0,58; РA(B1)=0,32
=0,58; РA(B1)=0,32
Ответ: Вероятность, что ответил отлично подготовленный студент равен 0,58, что ответил хорошо подготовленный студент – 0,32.
Заключение
Опередив свое время, преподобный Том Байес открыл миру одну из самых важных формул теории вероятностей. Эта формула использовалась в расчетах уже в начале 18 века, но, как утверждение было сформулировано только в конце этого же века Пьером-Симоном Лапласом. Формула Байеса применяется не только в математике и информатике, кибернетике, но и в философии, экономике, маркетинге, менеджменте различных областей нашей жизни.
Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной.
События, отражающие действие «причин», в данном случае обычно называют гипотезами, так как они – предполагаемые события, повлекшие данное. Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще), а условную - с учетом факта произошедшего события – апостериорной (насколько вероятна оказалась причина с учетом данных о событии). Таким образом, мы получили возможность прогнозирования на научной основе с учетом всех гипотез.
Можно также уточнять вероятность гипотезы, учитывая другие имеющиеся данные (другие произошедшие события). Для учета каждого следующего события нужно в качестве априорной вероятности гипотезы подставлять ее апостериорную вероятность с предыдущего шага.
Список использованной литературы:
Гмурман В. Е. Руководство к решению задач по теории вероятности и математической статистике: Учеб. пособие для студентов втузов М.:Высшая школа, 1979.- 400 с.
Вентцель Е. С., Овчаров Л. А. Теория вероятностей. М.: Наука, 1973.- 386с.
Емельянов Г. В., Скитович В. П. Задачник по теории вероятностей и математической статистике Л.: Изд-во Ленинград. ун-та, 1967.- 332 с.
Лозинский Н. С. Сборник задач по теории вероятностей и математической статистике: Учеб. пособие для студентов экономических специальностей вузов. - М.: Статистика, 1975.- 200 с.
Сборник задач по теории вероятностей, математической статистики м теории случайных функций. / Под ред. А. А. Свешникова.- М.: Наука, 1970.- 656 с.
Формула полной вероятности. Вероятность гипотез. Формулы Байеса. Составитель преподаватель кафедры высшей математики Ищанов Т.Р. Занятие №4., код доступа: http://ischanow.ru/node/25
2


 Получите свидетельство
Получите свидетельство Вход
Вход



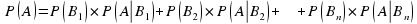
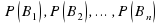 . Событие А может произойти только вместе с каким либо из событий В1,B2,B3,…Вn , которые назовем гипотезами. Тогда по формуле полной вероятности
. Событие А может произойти только вместе с каким либо из событий В1,B2,B3,…Вn , которые назовем гипотезами. Тогда по формуле полной вероятности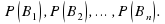
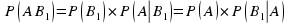
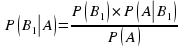
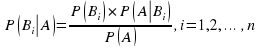
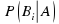 - вероятности гипотез
- вероятности гипотез 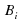 при наступлении события A называются апостериорными вероятностями;
при наступлении события A называются апостериорными вероятностями;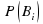 – вероятности гипотез называются априорными вероятностями.
– вероятности гипотез называются априорными вероятностями.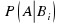 - вероятность наступления события A при истинности гипотезы
- вероятность наступления события A при истинности гипотезы 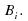
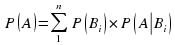
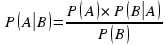
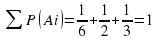
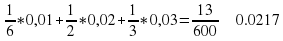
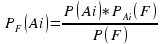
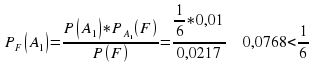
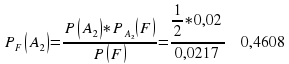
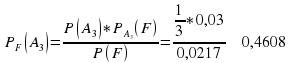
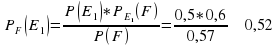
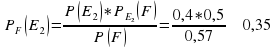
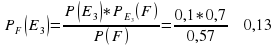
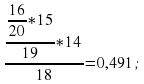 PB3(A)=
PB3(A)=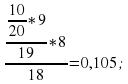 PB4(A)=
PB4(A)= 








 Материал для учителей математики "Теорема Байеса на службе прогноза развития современности" (36.33 КB)
Материал для учителей математики "Теорема Байеса на службе прогноза развития современности" (36.33 КB)
 0
0 1008
1008 33
33 Нравится
0
Нравится
0


