Тема: Применение теорем Чевы и Менелая
при решении геометрических задач
Учитель: Наследова Евгения Васильевна
1 квалификационная категория
Тюнева Надежда Васильевна
Высшая квалификационная категория
П.Светлый
2014 год
«Умение решать задачи - такое же практическое искусство, как умение плавать или бегать. Ему можно научиться только путем подражания или упражнения». (Д.Пойа)
Введение
Как показывает практика, геометрические задачи вызывают наибольшие затруднения у учащихся при сдаче ЕГЭ по математике. Итоги экзаменов показывают, что учащиеся плохо справляются с этими заданиями или вообще не приступают к ним. Можно выделить следующие недостатки в подготовке выпускников: формальное усвоение теоретического содержания курса геометрии, неумение использовать изученный материал в ситуации, которая отличается от стандартной. Для успешного выполнения этих заданий необходимы прочные знания основных геометрических фактов и опыт в решении геометрических задач. Одним из интереснейших разделов элементарной геометрии справедливо считается геометрия треугольника, так как несмотря на то, что треугольник едва ли не простейшая после отрезка фигура, он имеет много важных и интереснейших свойств, к которым сводятся свойства других, более сложных фигур. Среди теорем о треугольниках есть такие, изучение которых позволяет существенно расширить круг решения геометрических задач. Значение их состоит прежде всего в том, что из них или с их помощью можно вывести большинство теорем геометрии, они служат основой многих дальнейших выводов. Но в геометрии треугольника много и таких теорем, авторы которых остались в истории науки только «благодаря треугольникам». Речь идет о двух таких теоремах – теореме Чевы и теореме Менелая. Обе они имеют интересные и многочисленные приложения, позволяют легко и изящно решать целый класс задач.
Поэтому цель работы – сформулировать теоремы Чевы и Менелая и рассмотреть применение этих теорем к решению геометрических задач.
Задачей работы стало сравнение и выявление эффективности применения теорем Чевы и Менелая по сравнению с другими способами решения геометрических задач.
Представленная система заданий удовлетворяет следующим требованиям:
1) задачи разделены по видам: а) по характеру требования - задачи на доказательство, на вычисление или нахождение; б) по отношению к способу решения - стандартные и нестандартные;
2) включены задачи, при решении которых используются знания, полученные при изучении других разделов математики;
3) задачи с нестандартной постановкой вопроса, задачи, допускающие несколько способов решения;
Основная часть.
I. Теоремы Чевы и Менелая
1.1. Теорема Чевы.
Мы знаем, что медианы треугольника пересекаются в одной точке, биссектрисы треугольника пересекаются в одной точке, высоты треугольника (или их продолжения) пересекаются в одной точке. Рассмотрим  ABC и отметим на его сторонах BC, AC и AB (или их продолжениях) соответственно точки A
ABC и отметим на его сторонах BC, AC и AB (или их продолжениях) соответственно точки A ,B
,B и C
и C
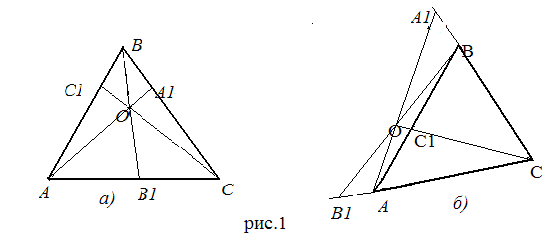
Поставим теперь общий вопрос: при каком расположении этих точек прямые AA , BB
, BB и
и
CC пересекутся в одной точке?
пересекутся в одной точке?
Ответ на этот вопрос нашел в 1678 году итальянский инженер-гидравлик Джованни Чева (1698г.-1734г.). Чева создал учение о секущих, положившее начало новой синтетической геометрии. (Отрезки, соединяющие вершины треугольника с точками на противолежащих сторонах, называют чевианами)
Сформулируем теорему Чевы.
Теорема. Пусть в 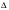 ABC на сторонах BC,AC и AB или их продолжениях взяты соответственно точки A
ABC на сторонах BC,AC и AB или их продолжениях взяты соответственно точки A ,B
,B и C
и C , не совпадающие с вершинами треугольника. Прямые
, не совпадающие с вершинами треугольника. Прямые
AA , CC
, CC и BB
и BB пересекаются в одной точке или параллельны тогда и только тогда, когда выполняется равенство
пересекаются в одной точке или параллельны тогда и только тогда, когда выполняется равенство

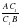 .
.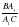 .
.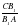 =1 (
=1 ( )
)
Следует заметить, что формулировка теоремы Чевы содержит два взаимно
обратных утверждения.
Примечание 1: равенство ( ) можно получить, заменив отношения отрезков в его левой части на отношение площадей.
) можно получить, заменив отношения отрезков в его левой части на отношение площадей.
Примечание 2: теорема Чевы остается справедливой для точек A ,B
,B ,C
,C , одна из которых принадлежит стороне треугольника, а две другие – продолжениям сторон.
, одна из которых принадлежит стороне треугольника, а две другие – продолжениям сторон.
Примечание 3: процедура составления ( ) не зависит от выбора «отправной» вершины и направления обхода, так как всегда будет получаться произведение, равное 1.
) не зависит от выбора «отправной» вершины и направления обхода, так как всегда будет получаться произведение, равное 1.
Примечание 4: и в случае внутренней точки O и в случае внешней точки O- условие ( )
)
Чевы можно записать также в виде  .
. .
. =1(
=1(
 )
)
Некоторые следствия из теоремы Чевы.
Следствие 1. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Следствие 2. Биссектрисы треугольника пересекаются в одной точке.
Следствие 3. Высоты треугольника (или их продолжения) пересекаются в одной точке (ортоцентре треугольника).
Следствие 4. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Следствие 5. Прямые, соединяющие вершины треугольника с точками, в которых вписанная окружность касается противоположных сторон, пересекаются в одной точке
1.2.Теорема Менелая.
Теорема Менелая красива и проста; она входит в золотой фонд древнегреческой математики. Название теорема получила в честь своего автора – древнегреческого математика и астронома Менелая Александрийского (примерно 100 г. н.э.). Во многих случаях эта теорема помогает очень легко и изящно решать достаточно сложные геометрические задачи.
Пусть на сторонах AB,BC и на продолжении стороны AC (либо на продолжениях сторон AB,BC и AC)  ABC взяты соответственно точки C
ABC взяты соответственно точки C ,A
,A и B
и B , не совпадающие с вершинами
, не совпадающие с вершинами  ABC. Точки A
ABC. Точки A ,B
,B ,C
,C лежат на одной прямой тогда и только тогда, когда выполняется равенство
лежат на одной прямой тогда и только тогда, когда выполняется равенство
 .
.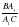 .
.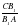 =1 (
=1 ( )
)
Следует отметить, что формулировка теоремы Менелая так же содержит два взаимно обратных утверждения.
Равенство Менелая аналогично условию Чевы, и его можно записывать, начиная с любой вершины треугольника в любом направлении ( по часовой стрелке, против часовой стрелки). Необходимо помнить, что при составлении равенства надо переходить от вершины к вершине через точку пересечения секущей линии с этой стороной или ее продолжением; заканчивать необходимо в той же вершине, с которой начали.
Обозначим R= 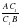 .
.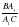 .
.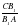 . Замечаем, что утверждение R=1 имеет место и в теореме Чевы, и в теореме Менелая. Поэтому справедливо следующее утверждение:
. Замечаем, что утверждение R=1 имеет место и в теореме Чевы, и в теореме Менелая. Поэтому справедливо следующее утверждение:
Пусть в треугольнике ABC на прямых AB,BC и AC взяты точки C ,A
,A ,B
,B , причем k из них лежат на сторонах треугольника и 3-k - на продолжениях сторон. Тогда
, причем k из них лежат на сторонах треугольника и 3-k - на продолжениях сторон. Тогда
а) точки A ,B
,B ,C
,C лежат на одной прямой тогда и только тогда, когда R=1 и k четно (теорема Менелая);
лежат на одной прямой тогда и только тогда, когда R=1 и k четно (теорема Менелая);
б) прямые AA , BB
, BB и СС
и СС  пересекаются в одной точке или параллельны тогда и только тогда, когда R=1 и k нечетно (теорема Чевы)
пересекаются в одной точке или параллельны тогда и только тогда, когда R=1 и k нечетно (теорема Чевы)
Примечание 5: можно вместо отношения 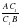 и других рассматривать отношения направленных отрезков, оно положительно, если векторы
и других рассматривать отношения направленных отрезков, оно положительно, если векторы  и
и  одинаково направлены, и отрицательно, если они противоположно направлены
одинаково направлены, и отрицательно, если они противоположно направлены
II. Применение теорем Чевы и Менелая для решения планиметрических задач.
Задача 1. В ABC на стороне AC взята точка M, а на стороне BC – точка K так, что AM: MC= 2:3, BK: KC= 4:3. В каком отношении AK делит отрезок BM?
ABC на стороне AC взята точка M, а на стороне BC – точка K так, что AM: MC= 2:3, BK: KC= 4:3. В каком отношении AK делит отрезок BM?
Решение:
1 способ. Через точку B проведем прямую a ll AC
AK a=P;
a=P;
 BKP ~
BKP ~  CKA
CKA

 BP=
BP=  AC.
AC.
 BOP~
BOP~ MOA
MOA
 =
=
В этом случае нужно увидеть подобные треугольники, для чего использовать дополнительное построение.
2 способ. Рассмотрим  MBC; прямую AK назовем секущей, так как она пересекает две стороны и продолжение третьей стороны треугольника MBC; A
MBC; прямую AK назовем секущей, так как она пересекает две стороны и продолжение третьей стороны треугольника MBC; A MC,O
MC,O BM, K
BM, K BC; A,O,K лежат на AK ( на одной прямой). По теореме Менелая
BC; A,O,K лежат на AK ( на одной прямой). По теореме Менелая  ,
,  ,
,
 =
= .
.
Ответ:  =
= .
.
Следует отметить, что теорема Менелая проста для применения, но здесь важно увидеть нужную конфигурацию - треугольник и секущую, причем такие, что два отношения в равенстве Менелая будут известны, тогда можно будет найти третье.
Задача 2 На сторонах треугольника ABC взяты соответственно точки C , A
, A ,B
,B ,так,
,так,
что AC : С
: С B= 2:1, BA
B= 2:1, BA :A
:A C=1:3, BB
C=1:3, BB
 CC
CC
 AA
AA =O.
=O.
Найти CB : B
: B A.
A.
Решение:
Так как отрезки BB , CC
, CC , AA
, AA пересекаются в одной точке O, то по теореме Чевы
пересекаются в одной точке O, то по теореме Чевы  .
.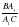 .
.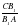 =1;
=1; 
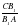 =1;
=1; 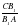 =
=
Ответ: 3:2
Задача 3 На стороне AC треугольника ABC взяты точки P и E , на стороне BC – точки M и K, причем AP: PE: EC= CK: KM: MB. Отрезки AM и BP пересекаются в точке O, отрезки AK и BE – в точке T. Докажите, что точки O, T и С лежат на одной прямой.
Дано:
 ABC; AP: PE: EC=CK: KM: MB=m:n:k
ABC; AP: PE: EC=CK: KM: MB=m:n:k
M, K BC, P, E
BC, P, E AC; AM
AC; AM BP= O; AK
BP= O; AK BE= T
BE= T
Доказать: O, T, C a
a
Доказательство.
Пусть луч CT AB=C
AB=C , CO
, CO AB=C
AB=C . Докажем, что точки C
. Докажем, что точки C и C
и C совпадают, это и будет означать, что O, T, C лежат на одной прямой.
совпадают, это и будет означать, что O, T, C лежат на одной прямой.
Так как CT AB=C
AB=C , BE
, BE AK
AK CC
CC = T, то по теореме Чевы
= T, то по теореме Чевы  ;
;
(1)
Так как CO AB=C
AB=C , AM
, AM BP= O, то СС
BP= O, то СС
 BP
BP AM=O, по теореме Чевы (2)
AM=O, по теореме Чевы (2)
Из (1) и (2) следует, что  , то есть точки С
, то есть точки С и C
и C делят отрезок AB в одном и том же отношении, начиная от точки A, а значит, С
делят отрезок AB в одном и том же отношении, начиная от точки A, а значит, С и C
и C совпадают. А это означает, что точки O, T, C лежат на одной прямой.
совпадают. А это означает, что точки O, T, C лежат на одной прямой.
Решение задач на пропорциональное деление отрезков в треугольнике.
Задача 4. Стороны треугольника 5, 6 и 7. Найдите отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.
Решение: пусть в треугольнике ABC AB = 5, BC = 7, AC = 6. Угол BAC лежит против большей стороны в треугольнике ABC, значит, угол BAC – больший угол треугольника. Центр вписанной окружности треугольника лежит на пересечении биссектрис. Пусть O -точка пересечения биссектрис. Необходимо найти AO:OD. Так как AD – биссектриса треугольника ABC, то  =
=  , то есть BD = 5k, DC = 6k. Так как BF – биссектриса треугольника ABC, то
, то есть BD = 5k, DC = 6k. Так как BF – биссектриса треугольника ABC, то  =
= , то есть AF = 5m, FC = 7m.
, то есть AF = 5m, FC = 7m.
Прямая BF пересекает две стороны и продолжение третьей треугольника ADC.
По теореме Менелая
 .
. .
. = 1,
= 1,  =
=  =
=  =
= 
Ответ: 11:7.
Задача 5. В треугольнике ABC, площадь которого равна 6, на стороне AB взята точка K, делящая эту сторону в отношении AK:BK = 2:3, а на стороне AC – точка L, делящая AC в отношении AL: LC = 5:3. Точка О пересечения прямых CK и BL удалена от прямой AB на расстояние  . Найдите длину стороны AB.
. Найдите длину стороны AB.
Решение:
1. Треугольники ABL и ABC имеют одинаковую высоту, проведенную из вершины B.
 =
=  =
=  =
=  , тогда S
, тогда S =
=  6 =
6 =  .
.
2. Прямая KC пересекает в треугольнике ABL две стороны и продолжение третьей. По теореме Менелая
 .
. .
. = 1,
= 1,  .
. .
. = 1,
= 1,  =
=  , то есть BО = 4p, ОL = p.
, то есть BО = 4p, ОL = p.
3. Треугольники KBQ и ABL имеют общий угол, значит,
 =
=  =
=  =
=  , тогда S
, тогда S =
=  .
. =
=  .
.
4. S =
= 

 KB =
KB =  =
= , 3m =
, 3m =  , тогда m =
, тогда m =  , AB=5m = 4.
, AB=5m = 4.
Итак, AB = 4.
Ответ: 4.
Решение задач, связанных с нахождением площадей
Задача 6. В 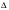 ABC на сторонах AB и BC взяты точки K и L так, что
ABC на сторонах AB и BC взяты точки K и L так, что  и
и  ,
,  ,
,  Найти
Найти  .
.
Решение: пусть  .
.
1) 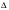 AOK и
AOK и 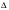 AOC имеют равные высоты,
AOC имеют равные высоты, 
 ;
;
2) 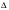 CAK и
CAK и 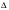 CBK имеют равные высоты,
CBK имеют равные высоты,  ;
;
3)  ; 4)
; 4)  ;
;
5) Рассмотрим 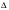 KBC и секущую AL; A
KBC и секущую AL; A KB, O
KB, O KC, L
KC, L BC.
BC.
По теореме Менелая  .
.

 ,
,  ,
, 
x=6 :  - верно.
- верно.

 , D
, D
 . Ответ: 21.
. Ответ: 21.
Задача 7. На сторонах AB и BC треугольника ABC взяты точки M и N соответственно. Отрезки AN и CM пересекаются в точке L. Площади треугольников AML , CNL и ALC равны соответственно 15, 48 и 40. Найти площадь треугольника ABC.
Решение: 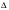 ALC и
ALC и 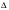 LCN , а также
LCN , а также 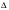 AML и
AML и 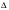 ALC имеют общие высоты, опущенные соответственно на стороны AN и MC. Отсюда следует, что площади этих треугольников относятся как соответствующие основания.
ALC имеют общие высоты, опущенные соответственно на стороны AN и MC. Отсюда следует, что площади этих треугольников относятся как соответствующие основания.
Рассмотрим 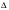 BMC и секущую AN.
BMC и секущую AN.
По теореме Менелая (1)
Рассмотрим 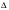 ABN и секущую MC.
ABN и секущую MC.
По теореме Менелая (2)
Вычитая из (2) соотношение (1) , получим
Так как  то
то  откуда 3AM=MB, а значит,
откуда 3AM=MB, а значит,
AM= MB=
MB= Отсюда следует, что S
Отсюда следует, что S составляет
составляет  часть площади треугольника ABC (они имеют общую высоту, проведенную из вершины С).
часть площади треугольника ABC (они имеют общую высоту, проведенную из вершины С).
Тогда  S
S = 4
= 4 S
S =(15+40)
=(15+40) .
.
Ответ: 220
Комбинированные задачи.
Задача 8. На сторонах AС и BC  взяты точки М и L так, что AM:MC=4:1, CL:LB=3:1. Отрезки AL и BM пересекаются в точке Q.
взяты точки М и L так, что AM:MC=4:1, CL:LB=3:1. Отрезки AL и BM пересекаются в точке Q.  .
.
1) Найти  ; 2) На АВ взяли точку N так, что CN – медиана ;
; 2) На АВ взяли точку N так, что CN – медиана ;  ,
,  . Найти
. Найти  .
.
Решение:
1) а) Рассмотрим  , BM – секущая,
, BM – секущая,
по теореме Менелая  ,
, 
б)  и
и  имеют равные высоты
имеют равные высоты
 . Так как
. Так как  ,
,

в) и
и  имеют равные высоты
имеют равные высоты
2) CN-медиана AN=NB. Найдем
AN=NB. Найдем 
а) ,
,  ;
;
б) ( имеют равные высоты),
( имеют равные высоты),
 ;
;  .
.
в) Рассмотрим 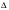 ABM и секущую NC.
ABM и секущую NC.
По теореме Менелая  ,
, 
 ,
,  ,
, 
 ,
, 
.
Ответ: 11 кв.ед.
кв.ед.
Задача 9. На сторонах АВ, ВС и СА треугольника АВС отмечены точки  и
и  соответственно так, что отрезки
соответственно так, что отрезки  и
и  пересекаются в одной точке Q, расположенной внутри треугольника АВС. Пусть Р – точка пересечения отрезков
пересекаются в одной точке Q, расположенной внутри треугольника АВС. Пусть Р – точка пересечения отрезков  и
и  . Доказать, что
. Доказать, что  .
.
Доказательство. Эта задача может быть решена несколькими способами, рассмотримрешение, использующее теоремы Менелая и Чевы. Если 
 , то утверждение задачи может быть легко доказано. Рассмотрим случай, когда прямые
, то утверждение задачи может быть легко доказано. Рассмотрим случай, когда прямые  и
и  пересекаются в точке М
пересекаются в точке М
По теореме Менелая для треугольников  и
и  имеем:
имеем:
 ,
,  , откуда
, откуда  ,
,
 .
.
Складывая эти равенства, получаем  (1)
(1)
По теореме Менелая для треугольников  и
и  имеем:
имеем:
 ,
, 
Учитывая, что  ,
,  , и складывая уравнения, получаем:
, и складывая уравнения, получаем:
. Из теоремы Чевы для треугольника АВС следует, что  .
.
Поэтому  (2)
(2)
Сравнивая (1) и (2) , получаем требуемое.
III. Применение теорем Менелая и Чевы в решении стереометрических задач.
Задача 1. На продолжении ребра АС правильной треугольной пирамиды ABCD с вершиной D взята точка K так, что КА:КС=3:4, а на ребре DC взята точка L так, что DL:LC=2:1. В каком отношении делит объем пирамиды плоскость, проходящая через точки B, L и К?
Дано:DABC – правильная пирамида,  ,
,  ,
,  ,
,  , BLK –
, BLK –
плоскость,  - объем верхней части пирамиды,
- объем верхней части пирамиды,  - объем нижней части пирамиды.
- объем нижней части пирамиды.
Найти:  .
.
Решение:
1) Построим сечение пирамиды DABC плоскостью BLK.
 соединяем,
соединяем,  соединяем,
соединяем,
 ,
,  соединяем,
соединяем, 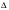 MLB - искомое сечение (рис.48).
MLB - искомое сечение (рис.48).
2) Найдем  , где
, где  - объем всей пирамиды.
- объем всей пирамиды.
Пусть BH – высота пирамиды DABC, проведенная из вершины В, но она – высота и BMDL.
 ; V=
; V= , V
, V =
= ;
;
;
 ,
,  - ?
- ?
3) Из 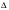 ADC:
ADC:  ,
,  ,
,  ,
,  .
.
По теореме Менелая ,  .
.
 ,
,  ,
,  .
.
(или: во всем объеме пирамиды 33 части, в верхней – 16, значит, 33-16=17 – частей
составляет  . Тогда
. Тогда  ) Ответ:
) Ответ:  .
.
Задача 2. Окружность с центром O, вписанная в треугольник ABC, касается стороны AC в точке K. Вторая окружность, также с центром O, пересекает все стороны треугольника ABC. Пусть E и F – её точки пересечения со сторонами соответственно AB и BC, ближайшие к вершине B; B1 и B2 – точки её пересечения со стороной AC, B1 – ближе к A. Докажите, что точки B, K и точка P пересечения отрезков B2E и B1F лежат на одной прямой.
Решение
Пусть L и M – точки касания вписанной окружности треугольника ABC со сторонами AB и BC соответственно. Тогда
AK = AL, BL = BM, CM = CK.
Из равенства прямоугольных треугольников OKB1, OKB2, OLE и OMF по катету и гипотенузе следует, что B1K = B2K = EL = FM. Поэтому
BE = BF, AE = AB2, CF = CB1.
Пусть отрезки B1F и B2E пересекают BK в точках P1 и P2 соответственно. Достаточно доказать, что точки P1 и P2 совпадают.
Рассмотрим треугольник ABK и прямую B2E. По теореме Менелая
Аналогично,
Следовательно, то есть точки P1 и P2 совпадают.
IV. Методы решения задач ЕГЭ 2014-2015 года
Задача 1 (Тренировочная работа № 8 по математике 26.02.2014)
На сторонах AD и BC параллелограмма ABCD взяты соответственно точки M и N , причём M — середина AD, а BN : NC =1:3.
а) Докажите, что прямые AN и AC делят отрезок BM на три равные части.
б) Найдите площадь четырёхугольника, вершины которого находятся в точках С, N и точках пересечения прямой BM c прямыми AN и AC , если площадь параллелограмма ABCD равна 48.
Решение.
Обозначим точки пересечения прямой BM c прямыми AN и AC буквами P и R соответственно. Пусть O – точка пересечения диагоналей параллелограмма. Тогда AO и BM — медианы треугольника ABD, значит,
Из подобия треугольников BPN и MPA находим, что Значит,
Из доказанного следует, что
б) Пусть площадь параллелограмма равна S . Из подобия треугольников MRA и BRC с
коэффициентом  следует, что высота треугольника BRC, проведённая к стороне BC,
следует, что высота треугольника BRC, проведённая к стороне BC,
составляет  высоты параллелограмма, проведённой к той же стороне. Следовательно,
высоты параллелограмма, проведённой к той же стороне. Следовательно,
площадь треугольника BRC равна
Аналогично найдём площадь треугольника BNP . Его высота, проведённая к BN , составляет  высоты параллелограмма, проведённой к стороне BC , а сама
высоты параллелограмма, проведённой к стороне BC , а сама
сторона BN в четыре раза меньше стороны параллелограмма BC. Поэтому
Следовательно, площадь четырёхугольника PRCN равна
Ответ: 14.
Задача 2 (18 задание КИМЫ ЕГЭ 2015 вариант 28)
На сторонах AB, BC и AC треугольника ABC взяты соответственно точки K, L и M,
причем AK : KB = 2 : 3, BL : LC = 1 : 2, CM : MA = 3 : 1. В каком отношении отрезок KL делит отрезок BM?
Решение. Изобразим треугольник ABC, разделим стороны на соответствующие части и отметим на сторонах точки K, L и M
(рис. 1).
Отработаем пропорцию, задав на каждой из сторон некую условную единицу измерения
и выразив длины соответствующих отрезков в этих единицах. А именно, пусть AM = x,
CM = 3x, AK = 2y, BK = 3y, BL = z, CL = 2z.
Рис. 1.
Так как задано много отношений и есть отрезки в треугольнике, то для удобства через вершину B проведем прямую, параллельную AC, и через E обозначим точку пересечения прямой KL с этой прямой, а через F - точку пересечения прямой KL с прямой AC (рис. 2). Получаем набор подобных треугольников.
Запишем информацию, вытекающую из подобий треугольников через точки L, K и O, т. е. подобий △BEL ∼ △CFL, △AKF ∼△BEK и △FMO ∼ △EBO. Для краткости и
эффективности обозначим AF = a, BE = b. Имеем (a + 4x)/b= 2,a/b=2/3,MO/BO=
(a + x)/b=a/b+x/b
Рис. 2.
Первое равенство дает: a/b+ 4x/b= 2 ⇐⇒x/b=1/3, откуда получаем, что MO : BO = 1 : 1.
Ответ: 1:1.
Задача 3 (18 задание КИМЫ ЕГЭ 2015 вариант 5)
Дан треугольник со сторонами AB = 4, BC = 5 и AC = 6.
Докажите, что прямая, проходящая через точку пересечения медиан и центр
вписанной окружности, параллельна стороне BC.
(b) Найдите длину биссектрисы треугольника ABC, проведеннойиз вершины A.
Изобразим треугольник с указанными сторонами, и отметим центр вписанной окружности
как точку пересечения его биссектрис и точку пересечения медиан.
Так как придется искать длину биссектрисы из вершины A, удобнее расположить эту
вершину сверху. Отметим точку P пересечения медиан и точку O пересечения биссектрис
Рис. 1.
Что может обеспечить параллельность OP и BC? Либо признаки параллельности двух
прямых, связанные с пересечением ее третьей прямой, либо отрезки этих прямых как соответственные стороны подобных треугольников, и удобнее так как такие треугольники несложно просматриваются -это △AOP и △ADM, где AD и AM есть биссектриса и
медиана треугольника ABC.
Для доказательства параллельности OP и DM достаточно убедиться в подобии этих треугольников. Угол с вершиной A у них общий, стало быть, достаточно доказать
одинаковую пропорциональность сторон AO, AD и AP, AM. Так как M – точка\ пересечения медиан, имеем AP : PM = 2 : 1. Отношение AO : OD можно обнаружить в треугольнике
ABD, в котором BO - биссектриса. Для нахождения отношения надо знать длину AD.
Отрезок BD - биссектриса в треугольнике ABC, и по ее свойству получаем BD : DC =
AB : AC = 2 : 3. Но BC = 5, следовательно, BD = 2, CD = 3. Теперь из треугольника ABD находим, что AO : OD = 2 : 1.
Тем самым требуемое равенство отношений доказано, треугольники
AOP и ADM подобны и OP װ DM.
Длину биссектрисы AM находим из треугольника ABM по теореме косинусов. Найдем
угол ABC из треугольника ABC по теореме косинусов:
36 = 16 + 25 − 2 ・ 4 ・ 5 ・ cosےABC, значит cosےABC =1/8. и AM2 = 16 + 4 + 2 ・ 4 ・
2 ・1/8= 18, т.е. AM = 3√2. Ответ: 3√2.
Заключение
Данная работа была посвящена двум таким теоремам – теореме Менелая и
теореме Чевы, которые позволяют решать многие, казалось бы, сложные математические задачи просто, красиво и понятно. Кроме того в рассмотренных задачах использовались
признаки подобия треугольников; свойства и признаки параллельных прямых;
метрические соотношения в треугольнике. Предложенный материал дал
возможность познакомиться с интересными, нестандартными вопросами геометрии,
еще одним методом решения геометрических задач.


 Получите свидетельство
Получите свидетельство Вход
Вход



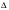 ABC и отметим на его сторонах BC, AC и AB (или их продолжениях) соответственно точки A
ABC и отметим на его сторонах BC, AC и AB (или их продолжениях) соответственно точки A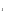 ,B
,B


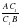 .
.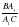 .
.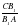 =1 (
=1 ( )
) ,B
,B








 Материал для учителей математики "Применение теоремы Чевы и Менелая при решении геометрических задач" (0.48 MB)
Материал для учителей математики "Применение теоремы Чевы и Менелая при решении геометрических задач" (0.48 MB)
 0
0 3366
3366 520
520 Нравится
0
Нравится
0


