Математическая логика

Презентация содержит информацию о законах логики.

Учитель информатики Б-Неклиновской сшМедведева И.Е.

Что такое алгебра логики?

Алгебра логики

раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Логическое высказывание

любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo.

Употребляемые в обычной речи слова и словосочетания

"не",   "и",   "или",  "если... , то",   "тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются   логическими связками .

Высказывания , образованные из других высказываний с помощью логических связок, называются   составными . Высказывания, не являющиеся составными, называются   элементарными .

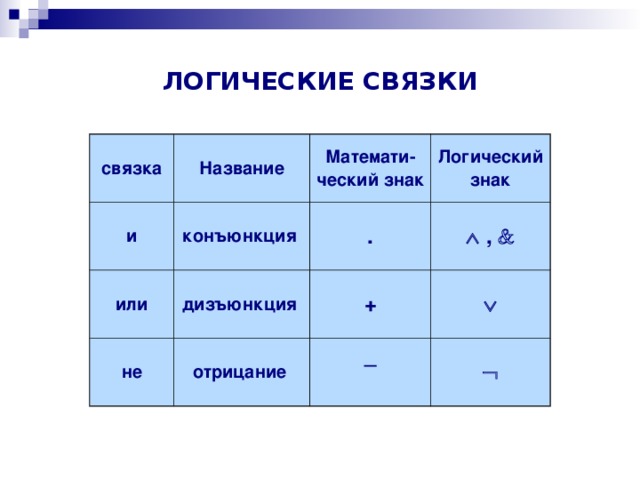
ЛОГИЧЕСКИЕ СВЯЗКИ

связка

Название

и

конъюнкция

Математи-ческий знак

или

не

Логический знак

.

дизъюнкция

отрицание

 , 

+



_



Определение логической формулы :

Всякая логическая переменная и символы "истина" (1) и "ложь" (0)

являются формулами.

Если  Х и  Y — формулы,

  то   X  Y  ,   X v Y  ,   X  Y  ,    X    

тоже формулы.

Никаких других формул в алгебре логики нет.



КОНЪЮНКЦИЯ (логическое умножение) x и y F(x,y) = x  y = x & y = x • y

х

0

у

0

х  y

0

1

0

1

1

0

0

0

1

1

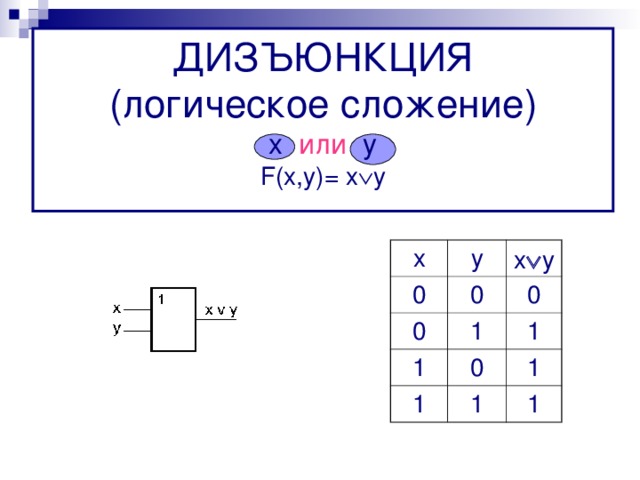
ДИЗЪЮНКЦИЯ ( логическое сложение ) х или у F(x,y)= x  y

х

0

у

0

0

х  у

0

1

1

1

1

0

1

1

1

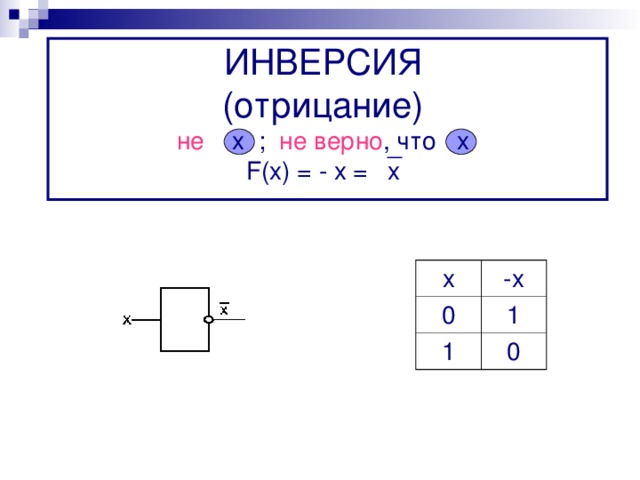
ИНВЕРСИЯ ( отрицание ) не х ; не верно , что х F(x) = - x =  x

х

0

-х

1

1

0

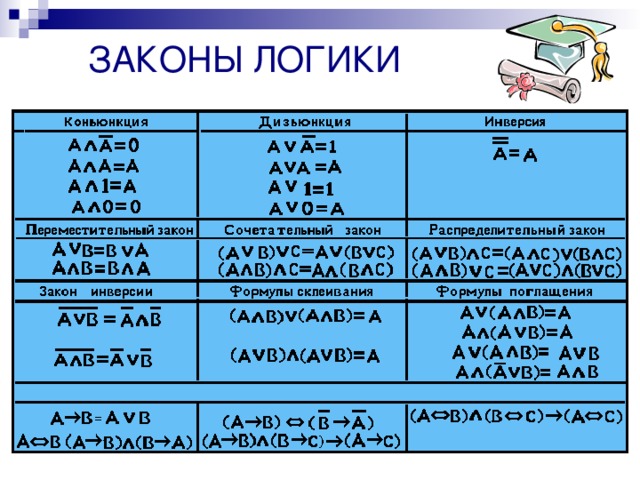
ЗАКОНЫ ЛОГИКИ

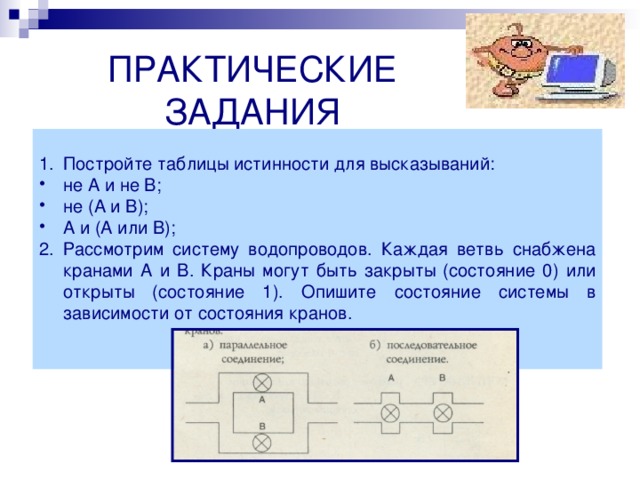
ПРАКТИЧЕСКИЕ ЗАДАНИЯ

• Постройте таблицы истинности для высказываний:

• не А и не В;
• не (А и В);
• А и (А или В);

• Рассмотрим систему водопроводов. Каждая ветвь снабжена кранами А и В. Краны могут быть закрыты (состояние 0) или открыты (состояние 1). Опишите состояние системы в зависимости от состояния кранов.

• Упростите приведённые формулы с помощью закона поглощения:

• А и (А или В) и (А или С)
• (А1 и А2) или (А1 и А2 и А3) или А1 или А2 или (А1 и А4 и В)

• Применяя законы логики упростите выражения:

• Не (не х и не у) или не х и не (х или не (не х или не у));
• ( х и не у и z ) или ( х и не ( у и z )) или ( х и у и z ) или ( х и не у ) ;

• В соответствии с законами логики определите значения высказываний :

• В соседней комнате сейчас находится какой-то человек или не верно, что в соседней комнате сейчас находится какой-то человек ;
• Неверно, что на столе лежит ручка или на столе лежит карандаш;
• Завтра будет вьюга и будет дождь или завтра не будет вьюги и будет дождь;
• Не является истинным, что Юра этого не делал.

ми

6. На основе логических рассуждений , описанных логическими формулами, или составлением таблиц истинности докажите законы :