
Логические основы построения компьютера
Презентацию подготовил учитель информатики МБОУ «Ясно-Полянская ООШ», Зубово-Полянского района, Республики Мордовия Куприянов А.С.
Презентация разработана по учебнику Н.В Макаровой для учащихся 9 классов.

История развития алгебры логики
В 1842 году английский математик Джорж Буль разработал математическую логику или алгебру логики, которую впоследствии стали называть «булевой алгеброй». В булевой алгебре высказывания принято обозначать прописными латинскими Буквами: А,В,X,Y. В алгебре Буля введены три основные логические операции с высказываниями: сложение, умножение, отрицание. Определены аксиомы (законы) алгебры логики для выполнения этих операций. Действия, которые производятся над высказываниями, записываются в виде логических выражений Спустя 100 лет алгебра логики стала основой теории цифровых вычислительных машин, ее используют в компьютерной логике, электронике, в основе всех микропроцессорных операций.
Джорж Буль
2 .11.1815г. -8.12.1864 г.

Термин «логика» происходит от древнегреческого Logos, означающего «слово, мысль, понятие, рассуждение, закон».
Алгебра логики – наука об операциях, аналогичных математическим, над высказываниями или над объектами, которые могут принимать только два значения – «ИСТИНА» или «ЛОЖЬ».
Примеры высказываний
Ложь
1
Все кошки серы
2
Париж –столица Франции
3
Сумма углов треугольника -180 градусов
4
10+5=14
5
Число 23 является простым
Истина
Истина
Ложь
Истина
Выражения, не являющиеся высказываниями
Не высказывание
1
2
Делайте утреннюю зарядку!
На улице идет дождь
3
4
Она красивая
Назовите устройства ввода информации
Не высказывание
Не высказывание
Не высказывание
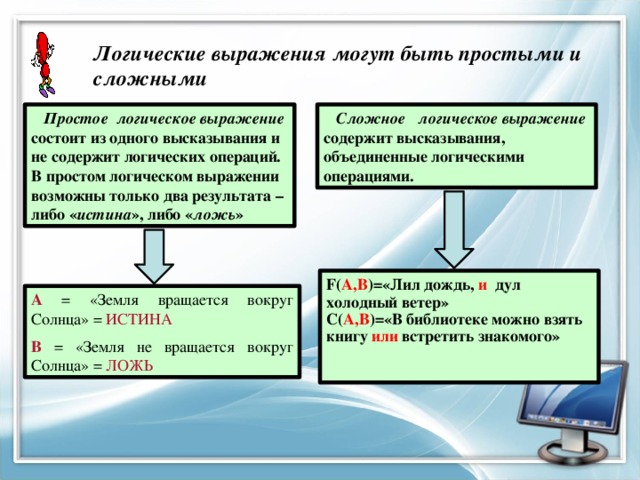
Логические выражения могут быть простыми и сложными
Простое логическое выражение
Сложное логическое выражение
состоит из одного высказывания и не содержит логических операций. В простом логическом выражении возможны только два результата – либо « истина », либо « ложь »
содержит высказывания, объединенные логическими операциями.
F( A,B )=«Лил дождь, и дул холодный ветер»
С( A,B )=«В библиотеке можно взять книгу или встретить знакомого»
А = «Земля вращается вокруг Солнца» = ИСТИНА
В = «Земля не вращается вокруг Солнца» = ЛОЖЬ
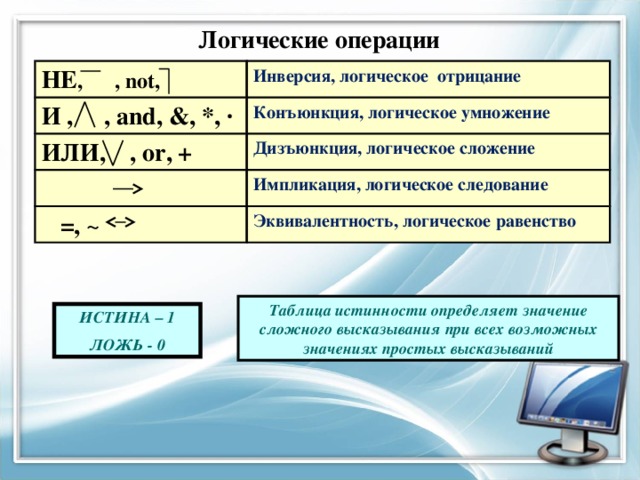
Логические операции
НЕ , , not,
И , , and, &, *, ·
Инверсия, логическое отрицание
ИЛИ, , or, +
Конъюнкция, логическое умножение
Дизъюнкция, логическое сложение
=, ~
Импликация, логическое следование
Эквивалентность, логическое равенство
Таблица истинности определяет значение сложного высказывания при всех возможных значениях простых высказываний
ИСТИНА – 1
ЛОЖЬ - 0

Инверсия - логическое отрицание
Логическое отрицание делает истинное высказывание ложным и, наоборот, ложное – истинным. От лат. inversio - переворачиваю
Таблица истинности функции логического отрицани я
A
0
А
1
1
0
A
А
истина
ложь
ложь
истина
или
ИСТИНА – 1 ЛОЖЬ - 0
В переводе на естественный язык «Не А», «Неверно, что А»
Пример : Даны высказывания
А – «Число 4 – четное» = ИСТИНА
Не А – «Неверно, что число 4 – четное» = ЛОЖЬ

Операция ИЛИ - логическое сложение,(дизъюнкция, объединение)
Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо истинно и А и В одновременно, и ложно тогда, когда аргументы А и В –ложны От лат. disjunctio – различаю.
В переводе на естественный язык «А или В»
Таблица истинности функции логического сложения
A
B
0
0
A B
0
1
0
1
0
1
1
1
1
1
Пример : Даны высказывания
А – «Число 4 – четное» = ИСТИНА
В – «Число 4– простое» = ЛОЖЬ
А или В – «Число 4 – четное или простое» - ИСТИНА
ИЛИ, , or, +

Операция И- логическое умножение (конъюнкция)
Результат операции И истинен тогда и только тогда, когда истинны одновременно высказывания А и В, и ложен во всех остальных случаях. От лат. conjunctio - связываю
Таблица истинности функции логического умножения
Пример : Даны высказывания
А – «Учитель должен быть умным» ИСТИНА
В – «Учитель должен быть справедливым» = ИСТИНА
А и В – «Учитель должен быть и умным, и справедливым» - ИСТИНА
A
B
0
A B
0
0
1
1
0
0
0
1
1
0
1
И , , and, &, *, ·
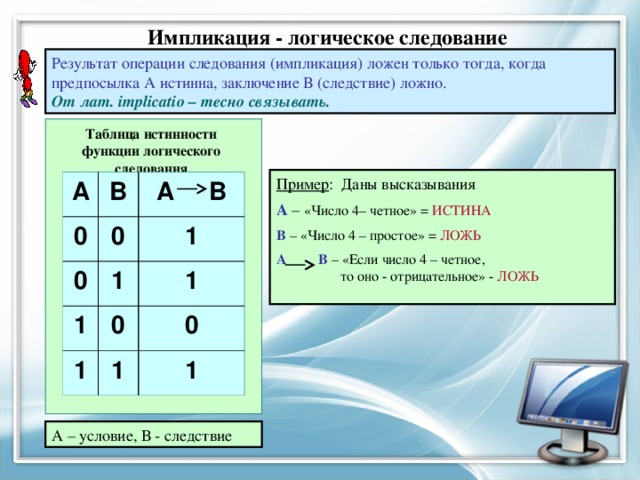
Импликация - логическое следование
Результат операции следования (импликация) ложен только тогда, когда предпосылка А истинна, заключение В (следствие) ложно. От лат. implicatio – тесно связывать.
Таблица истинности функции логического следования
Пример : Даны высказывания
А – «Число 4– четное» = ИСТИНА
В – «Число 4 – простое» = ЛОЖЬ
А В – «Если число 4 – четное, то оно - отрицательное» - ЛОЖЬ
A
B
0
A B
0
0
1
1
1
1
0
1
1
0
1
А – условие, В - следствие
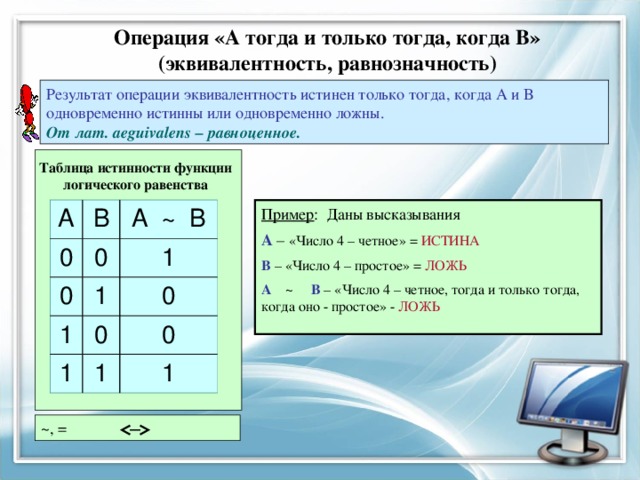
Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность)
Результат операции эквивалентность истинен только тогда, когда А и В одновременно истинны или одновременно ложны. От лат. aeguivalens – равноценное.
Таблица истинности функции логического равенства
Пример : Даны высказывания
А – «Число 4 – четное» = ИСТИНА
В – «Число 4 – простое» = ЛОЖЬ
А ~ В – «Число 4 – четное, тогда и только тогда, когда оно - простое» - ЛОЖЬ
A
B
0
A ~ B
0
0
1
1
1
1
0
0
1
0
1
~, =
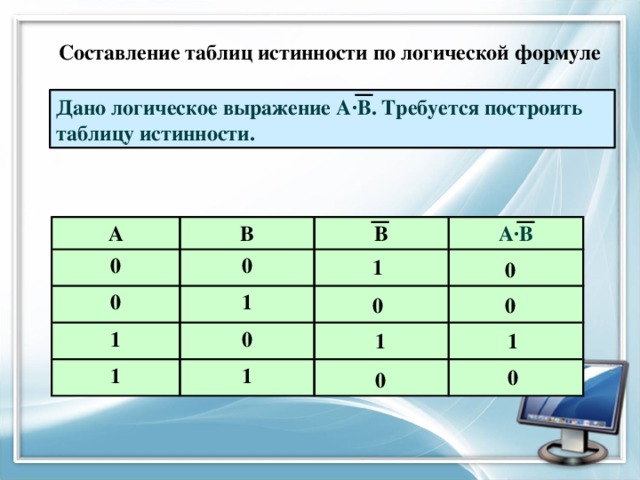
Составление таблиц истинности по логической формуле
Дано логическое выражение А∙В. Требуется построить таблицу истинности.
А
В
0
В
0
0
А∙В
1
1
1
0
1
1
0
0
0
1
1
0
0
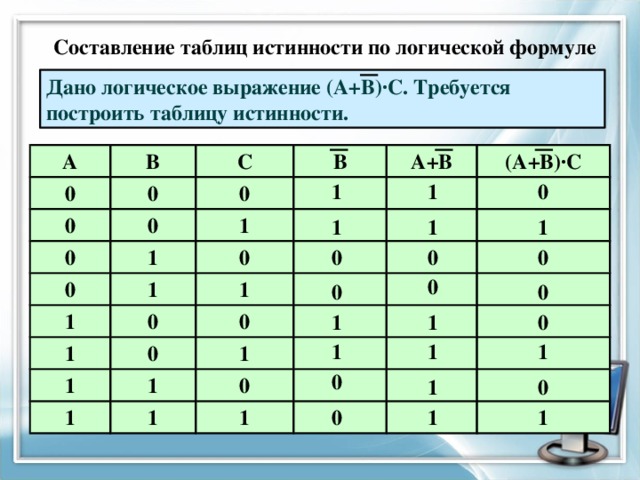
Составление таблиц истинности по логической формуле
Дано логическое выражение (А+В)∙С. Требуется построить таблицу истинности.
А
0
В
0
С
0
В
0
0
0
1
1
0
А+В
1
1
0
(А+В)∙С
0
1
1
0
0
1
1
1
1
0
1
1
1
0
1
1
1
1
0
0
0
0
0
0
1
1
0
1
1
1
0
1
0
0
1
1
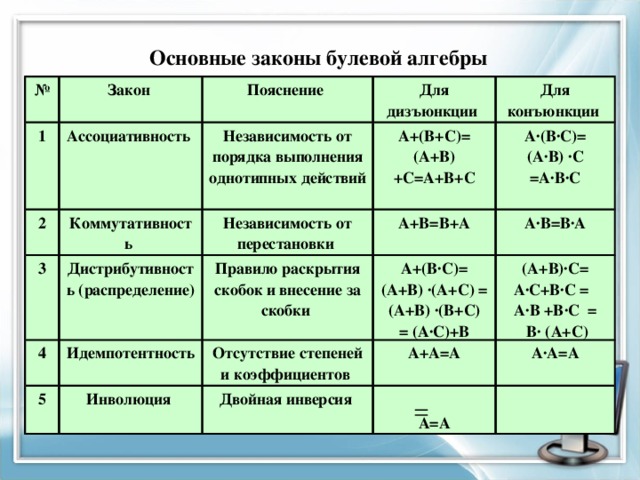
Основные законы булевой алгебры
№
Закон
1
Пояснение
2
Ассоциативность
Для дизъюнкции
Коммутативность
3
Независимость от порядка выполнения однотипных действий
Дистрибутивность (распределение)
4
Независимость от перестановки
Для конъюнкции
А+(В+С)= (А+В)+С=А+В+С
А∙(В∙С)= (А∙В) ∙С =А∙В∙С
Идемпотентность
А+В=В+А
Правило раскрытия скобок и внесение за скобки
5
А+(В∙С)= (А+В) ∙(А+С) = (А+В) ∙(В+С) = (А∙С)+В
А∙В=В∙А
Отсутствие степеней и коэффициентов
Инволюция
(А+В)∙С= А∙С+В∙С = А∙В +В∙С = В∙ (А+С)
А+А=А
Двойная инверсия
А∙А=А
А=А

Основные законы булевой алгебры (продолжение)
№
6
Закон
Действие с абсолютно –истинными высказываниями
7
Пояснение
Для дизъюнкции
Действие с абсолютно –ложными высказываниями
8
Законы де Моргана
9
А+1=1
Для конъюнкции
А∙1=А
А+0=А
Закон исключенного третьего и закон противоречия
Отрицание одновременной истинности
10
А+В=А+В
А∙0=0
11
Поглощение
А∙В=А+В
А+А=1
Поглощения отрицания
А∙А=0
А+А∙В=А
А+А∙В=А+В
А∙(А+В)=А
А∙(А+В)=А∙В
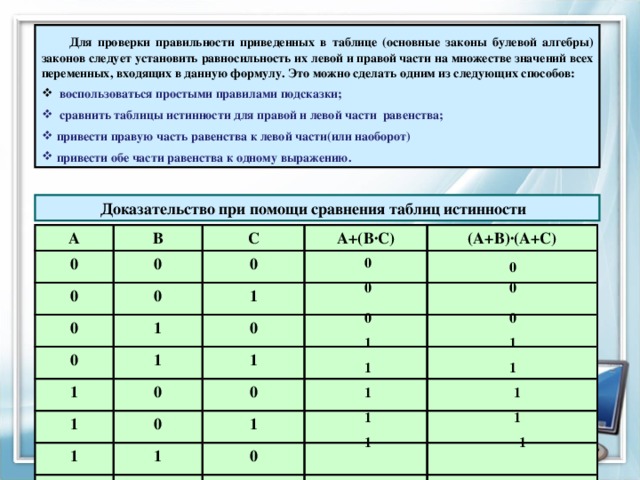
Для проверки правильности приведенных в таблице (основные законы булевой алгебры) законов следует установить равносильность их левой и правой части на множестве значений всех переменных, входящих в данную формулу. Это можно сделать одним из следующих способов:
- воспользоваться простыми правилами подсказки;
- сравнить таблицы истинности для правой и левой части равенства;
- привести правую часть равенства к левой части(или наоборот)
- привести обе части равенства к одному выражению.
Доказательство при помощи сравнения таблиц истинности
А
0
В
0
0
С
0
А+(В∙С)
0
0
(А+В)∙(А+С)
1
1
0
1
0
1
1
0
1
1
0
0
1
1
1
0
1
1
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
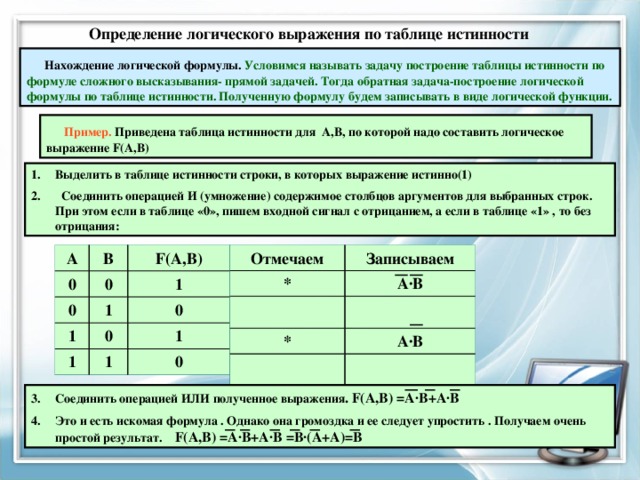
Определение логического выражения по таблице истинности
Нахождение логической формулы. Условимся называть задачу построение таблицы истинности по формуле сложного высказывания- прямой задачей. Тогда обратная задача-построение логической формулы по таблице истинности. Полученную формулу будем записывать в виде логической функции.
Пример. Приведена таблица истинности для А,В, по которой надо составить логическое выражение F(A,B)
- Выделить в таблице истинности строки, в которых выражение истинно(1)
- Соединить операцией И (умножение) содержимое столбцов аргументов для выбранных строк. При этом если в таблице «0», пишем входной сигнал с отрицанием, а если в таблице «1» , то без отрицания:
Отмечаем
A
*
Записываем
0
B
А∙В
F(A,B)
0
*
0
1
1
1
А∙В
1
0
0
1
1
0
- Соединить операцией ИЛИ полученное выражения . F(А,В) =А∙В+А∙В
- Это и есть искомая формула . Однако она громоздка и ее следует упростить . Получаем очень простой результат. F(А,В) =А∙В+А∙В =В∙(А+А)=В
Логические элементы и основные логические устройства компьютера.
Логический элемент – это электронное устройство, выполняющее одну из основных логических операций: И, ИЛИ, НЕ. Условные обозначения логических элементов являются стандартными и используются при составлении логических схем компьютера.
А
А
А или В
&
А и В
1
1
А
не А
В
В
На вход логического элемента поступают эклектические сигналы высокого и низкого уровней напряжения, которые интерпретируются в зависимости от реализуемых функций и на выход выдается один выходной сигнал также либо высокого, либо низкого уровня. Эти уровни соответствуют одному из состояний двоичной системы:1- ИСТИНА, 0-ЛОЖЬ.
Из логических элементов составляются электронные логические схемы , выполняющие более сложные логические операции. Тысячи микроскопических электронных переключателей в кристалле интегральной схемы сгруппированы в системы, выполняющие логические и арифметические операции над двоичными числами. Соединенные в различные комбинации, логические элементы дают возможность компьютеру решать сложнейшие задачи с помощью закодированных импульсов его двоичного языка.
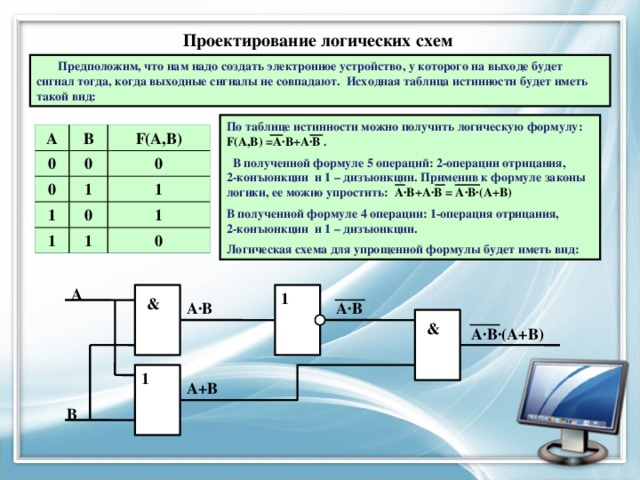
Проектирование логических схем
Предположим, что нам надо создать электронное устройство, у которого на выходе будет сигнал тогда, когда выходные сигналы не совпадают. Исходная таблица истинности будет иметь такой вид:
По таблице истинности можно получить логическую формулу: F(А,В) =А∙В+А∙В .
В полученной формуле 5 операций: 2-операции отрицания, 2-конъюнкции и 1 – дизъюнкции. Применив к формуле законы логики, ее можно упростить: А∙В+А∙В = А∙В∙(А+В)
В полученной формуле 4 операции: 1-операция отрицания, 2-конъюнкции и 1 – дизъюнкции.
Логическая схема для упрощенной формулы будет иметь вид:
A
B
0
F(A,B)
0
0
1
0
1
0
1
1
1
1
0
А
1
&
А∙В
А∙В
&
А∙В∙(А+В)
1
А+В
В
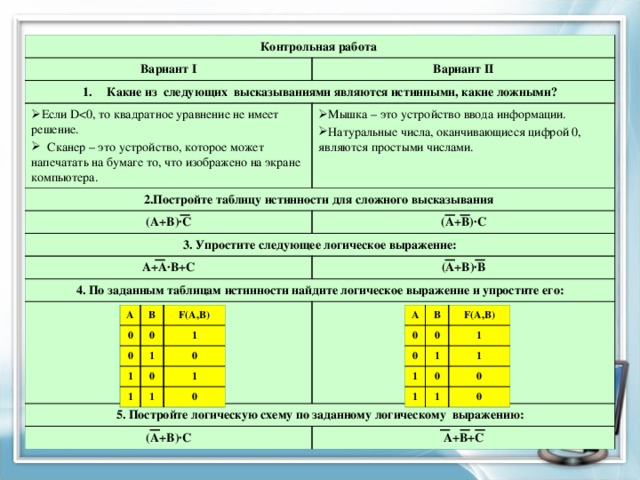
Контрольная работа
Вариант I
- Какие из следующих высказываниями являются истинными, какие ложными?
Вариант II
- Если D
- Сканер – это устройство, которое может напечатать на бумаге то, что изображено на экране компьютера.
- Мышка – это устройство ввода информации.
- Натуральные числа, оканчивающиеся цифрой 0, являются простыми числами.
2.Постройте таблицу истинности для сложного высказывания
(А+В)∙С
3. Упростите следующее логическое выражение:
(А+В)∙С
А+А∙В+С
4. По заданным таблицам истинности найдите логическое выражение и упростите его:
(А+В)∙В
5. Постройте логическую схему по заданному логическому выражению:
(А+В)∙С
А+В+С
A
A
0
0
B
B
0
F(A,B)
0
0
F(A,B)
0
1
1
1
1
1
1
1
1
1
0
0
0
1
0
1
1
0
0

Литература
- Информатика и ИКТ. Учебник 8-9 класс/ Под редакцией Н.В. Макаровой . –СПб.: Питер, 2010. -416 страниц
- Информатика и ИКТ. Практикум 8-9 класс/ Под редакцией Н.В. Макаровой . –СПб.: Питер, 2010. -384 страницы
Интернет ресурсы
- http://gym1505.ru/node/15432
- http://www.krugosvet.ru/enc/nauka_i_tehnika/matematika/BUL_DZHORDZH.html
- http://pda.privet.ru/user/na-tusya
- http://pedsovet.su/load/321-1-0-30252


 Получите свидетельство
Получите свидетельство Вход
Вход






























 Логические основы построения компьютера (0.58 MB)
Логические основы построения компьютера (0.58 MB)
 0
0 2056
2056 266
266 Нравится
0
Нравится
0


