Логические основы построения компьютера
Основные понятия алгебры логики
Логика – наука, изучающая законы и формы мышления.
Алгебра логики – раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений и логических операций над ними.
Логическое высказывание – любое повествовательное предложение в отношении которого можно однозначно сказать истинно оно или ложно.
истина – 1 ложь – 0
Установите какие из следующих предложений являются логическими высказываниями, а какие – нет (объясните почему):
- Солнце есть спутник Земли
- 6:2+9
- Санкт-Петербург расположен на Неве
- Как вас зовут?
- Музыка Баха очень сложна
- Запишите в тетради определение
- Если сумма квадратов катетов равна квадрату гипотенузы, то это прямоугольный треугольник
10 Квадрат это ромб В городе Иваново живут только граждане России После вторника будет воскресенье " width="640"
Даны логические высказывания. Определить истинны они или ложны.
- Земля – планета Солнечной системы
- За зимой наступает весна
- 3+6 10
- Квадрат это ромб
- В городе Иваново живут только граждане России
- После вторника будет воскресенье
Простое высказывание – это высказывание, которое содержит только одну простую мысль.
Например: Квадрат это ромб
Сложное высказывание – это высказывание, которое содержит несколько простых мыслей, соединенных между собой с помощью логических операций.
Например: Лил дождь, и дул холодный ветер
Значение сложного высказывания можно определить только с помощью специальной таблицы – таблицы истинности .
Таблица истинности – это таблица, в которой перечислены все возможные значения входящих простых логических высказываний и соответствующие им значения сложного логического высказывания
Количество строк ( q ) в таблице можно определить по формуле: q = 2 n , где n – это количество простых высказываний, входящих в сложное высказывание
Логические операции
1. Инверсия (логическое отрицание) – определяется над одним простым или сложным ЛВ. К исходному ЛВ добавляется частица «НЕ» (не A ).
Обозначение: не, not, , A
Таблица истинности:
A
0
A
1
1
0
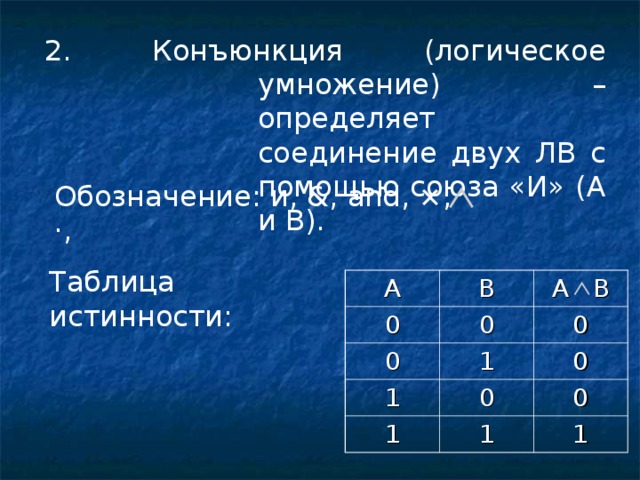
2. Конъюнкция (логическое умножение) – определяет соединение двух ЛВ с помощью союза «И» ( A и B ).
Обозначение: и, &, and, ×, · ,
Таблица истинности:
A
0
B
0
0
A B
0
1
1
1
0
0
0
1
1
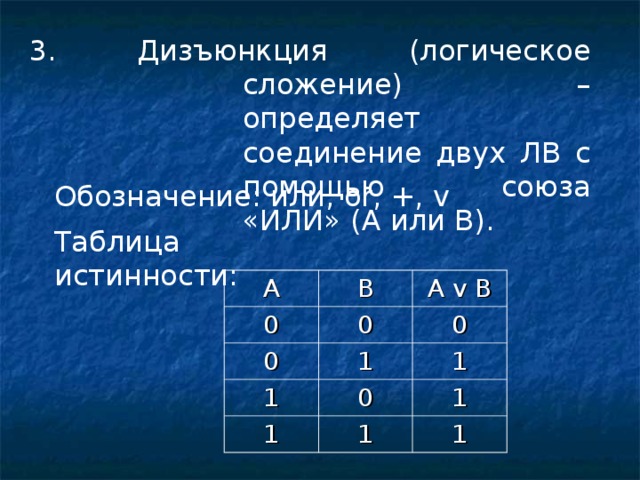
3. Дизъюнкция (логическое сложение) – определяет соединение двух ЛВ с помощью союза «ИЛИ» ( A или B ).
Обозначение: или, or, +, v
Таблица истинности:
A
0
B
A v B
0
0
0
1
1
1
0
1
1
1
1
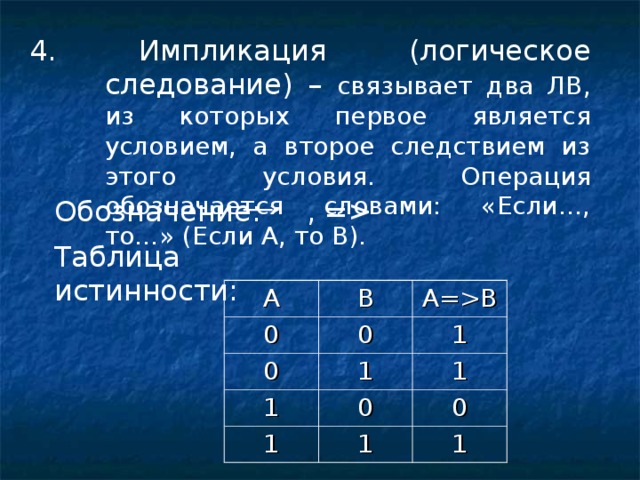Таблица истинности: A 0 B A=B 0 0 1 1 1 1 0 1 0 1 1 " width="640"
4 . Импликация (логическое следование) – связывает два ЛВ, из которых первое является условием, а второе следствием из этого условия. Операция обозначается словами: «Если…, то…» ( Если А, то В ) .
Обозначение: , =
Таблица истинности:
A
0
B
A=B
0
0
1
1
1
1
0
1
0
1
1
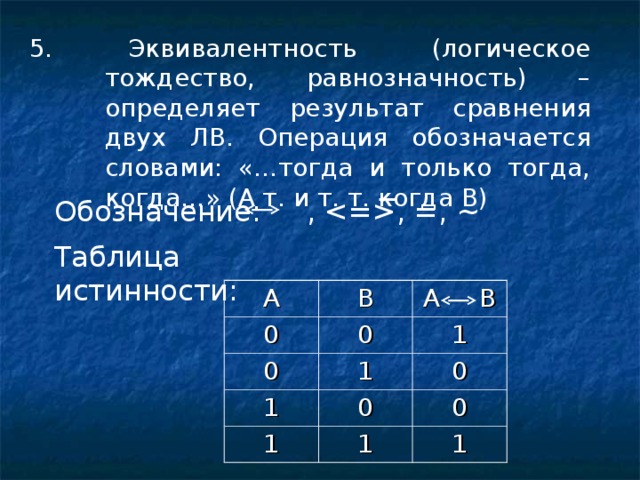
5 . Эквивалентность (логическое тождество, равнозначность) – определяет результат сравнения двух ЛВ. Операция обозначается словами: «…тогда и только тогда, когда…» (А т. и т. т. когда В)
Обозначение: , , =, ~
Таблица истинности:
A
0
B
0
0
A B
1
1
1
1
0
0
1
0
1
B = ¬AvB A B = (¬AvB)&(¬BvA) Это первые из основных законов алгебры логики " width="640"
Импликацию и эквивалентность можно заменить сочетанием первых трех операций:
A = B = ¬AvB
A B = (¬AvB)&(¬BvA)
Это первые из основных законов алгебры логики
Приоритет выполнения логических операций:
- 1) инверсия (отрицание)
- 2) конъюнкция (умножение)
- 3) дизъюнкция (сложение)
- 4) импликация (следование)
- 5) эквивалентность (тождество)
Для изменения указанного порядка выполнения логических операций используются скобки
=5 Теннисист Кафельников не проиграл финальную игру Число n делится на 2 На контрольной работе каждый ученик писал своей ручкой Мишень поражена вторым выстрелом Кит это млекопитающее " width="640"
Задание 1: Сформулируйте отрицания следующих высказываний:
- Эльбрус – высочайшая горная вершина Европы
- 2 =5
- Теннисист Кафельников не проиграл финальную игру
- Число n делится на 2
- На контрольной работе каждый ученик писал своей ручкой
- Мишень поражена вторым выстрелом
- Кит это млекопитающее
Задание 2: Найдите значение логических выражений
2
1
0
а ) (1&1)&0 =
1) 1 &1 = 1
2 ) 1 &0 = 0
5
1
2
3
4
б) ((1 v 0)&(1&1))&(0 v 1) =
1
1) 1 v0 = 1
2 ) 1 &1 = 1
3 ) 1 &1 = 1
4 ) 0v1 = 1
5 ) 1 &1 = 1
4
1
2
3
в) ((1 &1) v 0)&(0 v 1) =
1
1) 1 &1 = 1
2 ) 1 v0 = 1
3 ) 0v1 = 1
4 ) 1 &1 = 1
3
2
1
5
4
0
г) ((0 v 0)&(1& 0 )) v (0&1) =
1) 0v0 = 0
2 ) 1 &0 = 0
3 ) 0&0 = 0
4 ) 0&1 = 0
5 ) 0v0 = 0
(A&C)v(B&C) г) (A&B)vC (AvC)&(A&B) " width="640"
Задание 3: Даны простые ЛВ. Определить значение сложных ЛВ.
A={2x2=4}, B={2=3}, C={4
а) ¬A
б) ¬ ( A&B)
в) (AvB)&C = (A&C)v(B&C)
г) (A&B)vC (AvC)&(A&B)
Построение таблицы истинности сложных ЛВ:
- 1) определить число простых ЛВ ( n )
- 2) определить число строк в таблице истинности ( q=2 n )
- 3) записать все возможные значения простых ЛВ
- 4) определить количество логических операций и их порядок
- 5) записать логические операции в таблицу истинности и определить для каждой значение
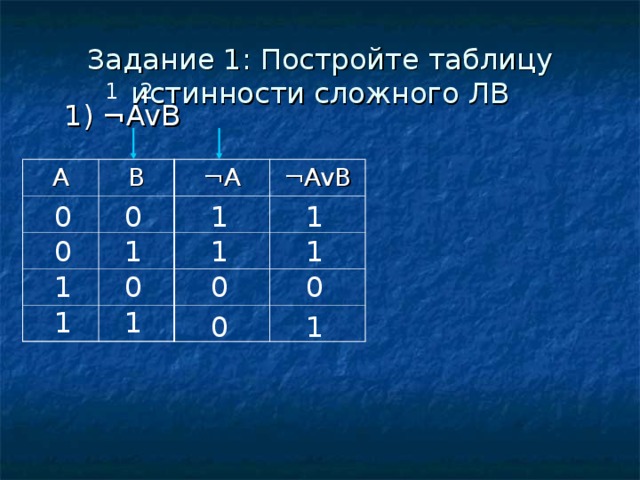
Задание 1: Постройте таблицу истинности сложного ЛВ
1
2
1) ¬AvB
A
¬A
¬AvB
B
1
1
0
0
0
1
1
1
0
0
1
0
1
1
0
1
5
1
4
3
2
2) (¬AvB)&(¬BvA)
A
B
¬A
¬AvB
¬B
¬BvA
(¬AvB)&(¬BvA)
0
1
1
1
1
0
1
1
0
0
1
0
0
1
1
0
0
1
0
1
0
1
1
0
1
1
0
1
1
3
2
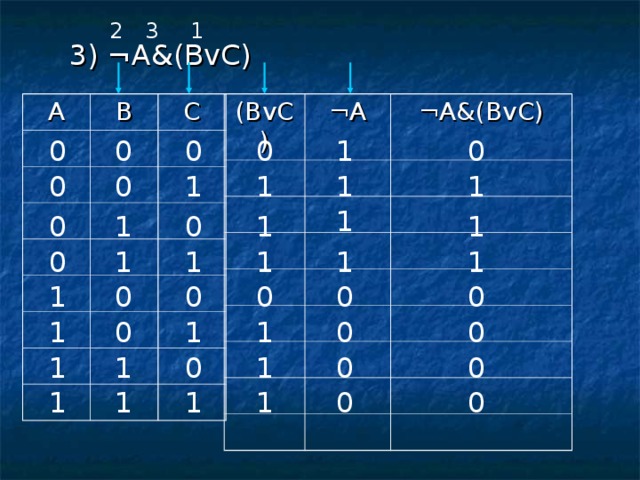
3) ¬A&(BvC)
A
(BvC)
B
¬A
C
¬A&(BvC)
0
0
0
0
1
0
1
0
1
0
1
1
1
1
1
1
0
0
0
1
1
1
1
1
1
0
0
0
0
0
1
1
0
1
0
0
1
0
1
1
0
0
1
0
1
1
1
0
3
2
1
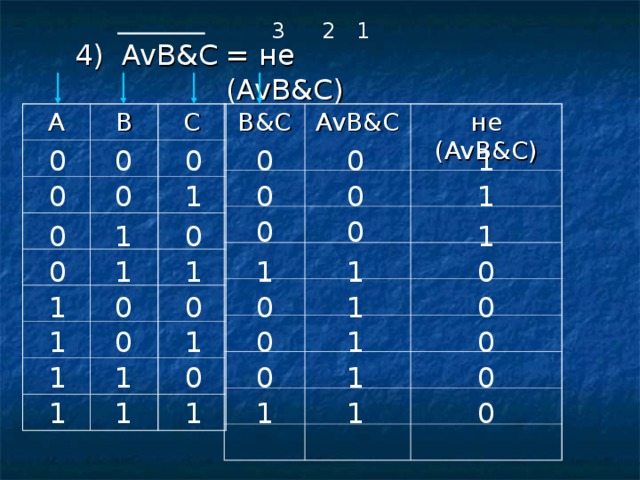
= не ( AvB&C )
4) AvB&C
B&C
A
AvB&C
B
C
не ( AvB&C )
0
1
0
0
0
0
0
1
0
0
0
1
0
0
1
1
0
0
0
1
0
1
1
1
1
0
0
1
0
0
0
1
0
1
1
0
0
1
0
1
1
0
1
1
1
1
1
0
Задание 2: Постройте таблицы истинности сложных ЛВ и сравните их:
1) А и В или С и А
2) (А или В) и (А или С)
3) А и (В или С)
4) А или (не В или не С)
5) не (не A и не ( B и C ))
В) и (А или В) 3) А и В (A или B ) 4) А и B и (А и В) 5) A и ( B и (А или В)) " width="640"
Задание 3: Определите с помощью таблиц истинности, какие из ЛВ являются тождественно-истинными:
1) А и А или В и (А и В или В)
2) ((А или В) = В) и (А или В)
3) А и В (A или B )
4) А и B и (А и В)
5) A и ( B и (А или В))
Построение ЛВ по таблице истинности:
- 1) записать логическое умножение всех простых ЛВ для каждой строки, где сложное ЛВ = 1 (если значение простого ЛВ = 0, то берется его отрицание)
- 2) логически сложить, полученные выражения
Составьте сложное ЛВ по таблице истинности
А)
A
0
B
C
0
0
F
0
0
0
0
1
0
1
1
1
0
1
0
1
1
1
0
0
1
0
0
1
1
1
0
1
1
0
1
0
не A и не B и С
не A и B и не С
A и не B и С
(не A и не B и С) или (не A и B и не С) или ( A и не B и С)
Б)
A
0
B
C
0
0
F
0
0
0
0
1
1
1
0
1
1
0
0
1
0
1
0
1
0
1
0
1
1
1
0
0
1
1
0
1
не A и не B и не С
не A и B и С
A и B и С
(не A и не B и не С) или (не A и B и С) или ( A и B и С)
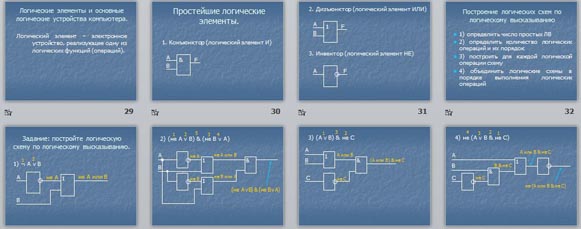
Логические элементы и основные логические устройства компьютера.
Логический элемент – электронное устройство, реализующее одну из логических функций (операций).
Простейшие логические элементы.
1. Конъюнктор (логический элемент И)
A
F
&
B
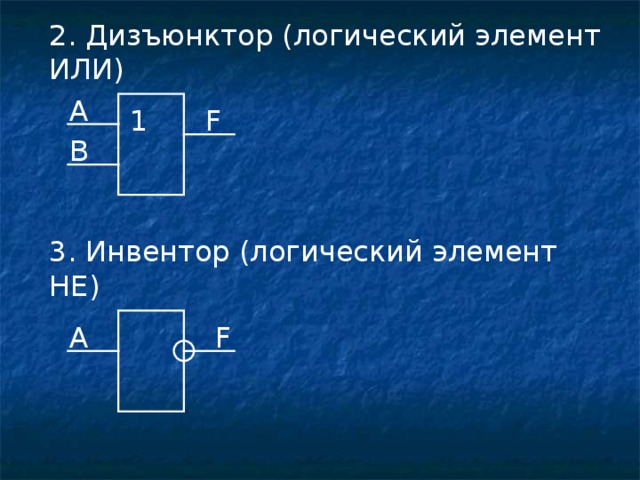
2 . Дизъюнктор (логический элемент ИЛИ)
A
F
1
B
3. Инвентор (логический элемент НЕ)
A
F
Построение логических схем по логическому высказыванию
- 1) определить число простых ЛВ
- 2) определить количество логических операций и их порядок
- 3) построить для каждой логической операции схему
- 4) объединить логические схемы в порядке выполнения логических операций
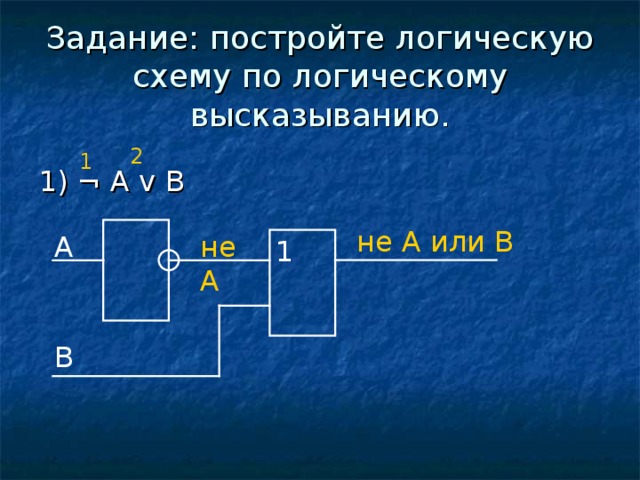
Задание: постройте логическую схему по логическому высказыванию.
2
1
1) ¬ A v B
не А или В
не А
A
1
В
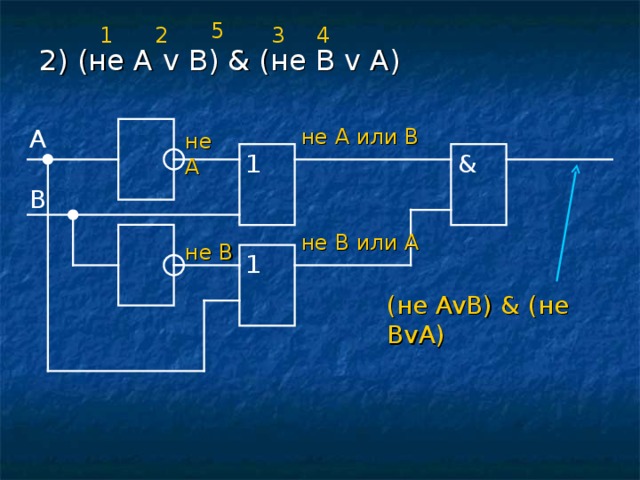
5
3
2
1
4
2) (не A v B) & ( не B v A)
A
не A или B
не A
&
1
B
не В или А
не B
1
(не AvB) & ( не BvA)
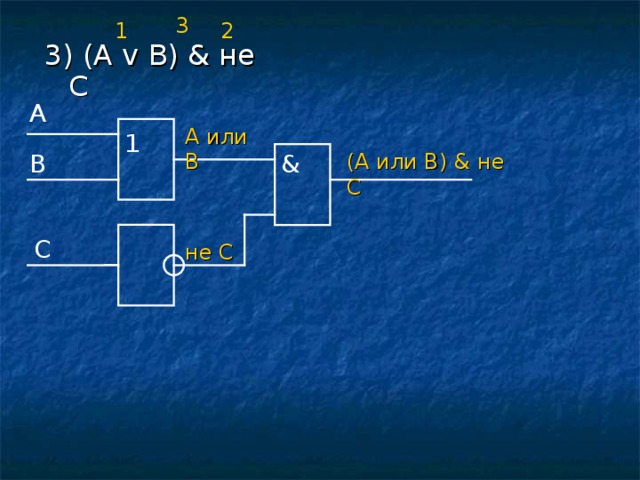
3
2
1
3) (A v B) & не C
A
А или В
1
B
&
(A или B) & не C
С
не С
4
2
3
1
4) не (A v B & не C)
А или В & не C
A
1
B
B & не C
&
не С
С
не (А или В & не C )
2
1
3
5) A & B v C & A
С
С и А
&
A и B или С и А
1
A
A и В
&
B
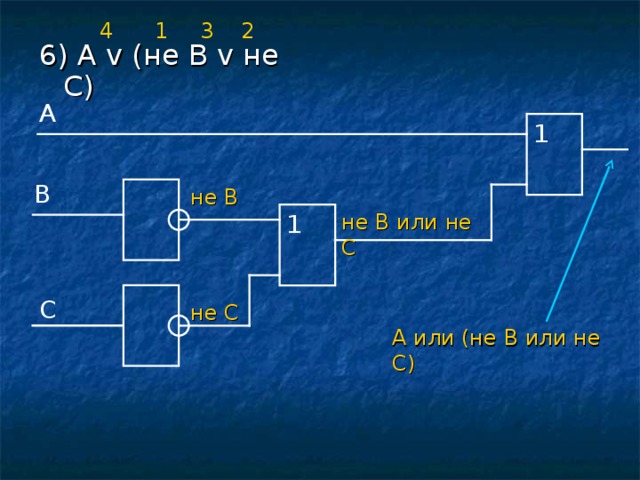
3
2
1
4
6) A v ( не B v не C)
A
1
B
не В
не B или не C
1
С
не С
А или (не B или не C )
Построение логического высказывания по логической схеме
- 1) на выходе каждого логического элемента записать результат логической операции
- 2) записать получившуюся формулу на выходе последнего элемента
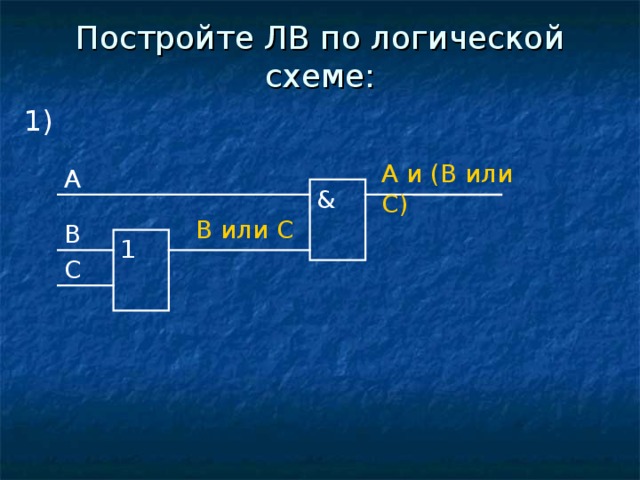
Постройте ЛВ по логической схеме:
1)
A и (B или C)
A
&
B или C
B
1
C
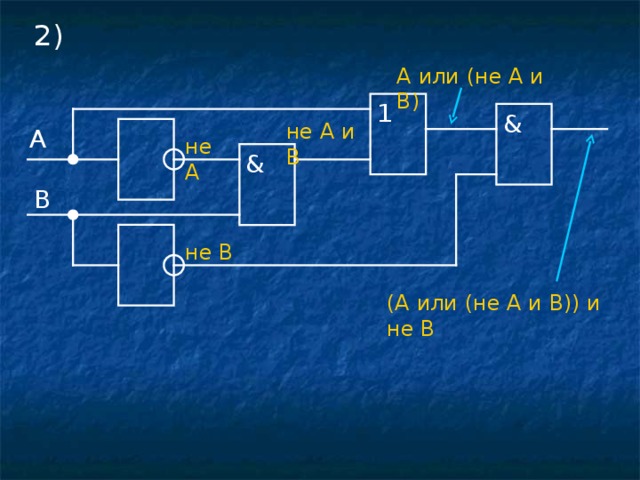
2 )
A или (не A и B )
1
&
не A и B
A
не A
&
B
не B
(A или (не A и B ) ) и не B
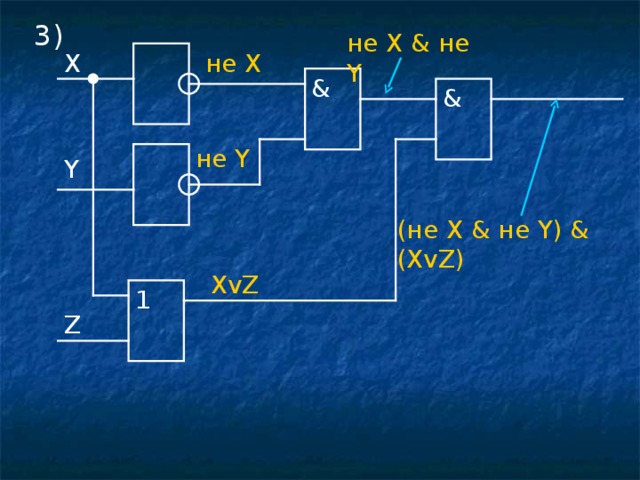
3)
не X & не Y
не X
X
&
&
не Y
Y
( не X & не Y) & (XvZ)
XvZ
1
Z
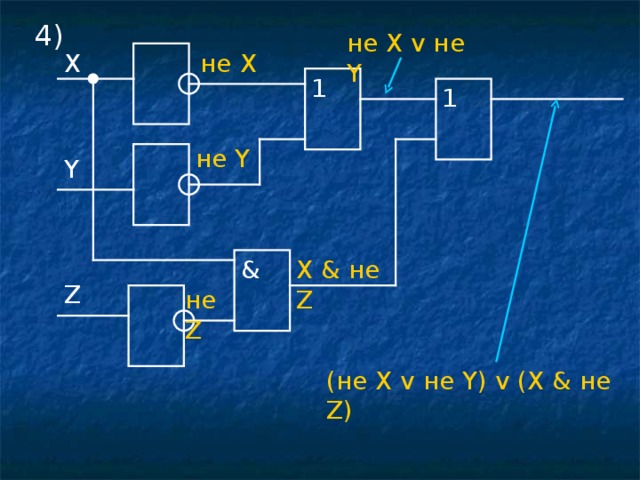
4)
не X v не Y
не X
X
1
1
не Y
Y
X & не Z
&
Z
не Z
( не X v не Y) v (X & не Z)
Работа Рыженко Елены Владимировны, учителя информатики и математики МБОУ г. Астрахани « СОШ № 64»
Получите свидетельство
Вход
Логические основы построения компьютера (2.08 MB)
0
717
21
Нравится
0
