Логика и компьютер

ЛОГИКА И КОМПЬЮТЕР

Выполнила

Учитель информатики :

Позднякова Наталия Сергеевна

Логика в информатике – это те отрасли знания и направления исследований, в которых логика применяется в информатике и искусственном интеллекте. В информатике логика оказалась гораздо более эффективной, чем это было в математике.

Основные направления прикладного использования логики в информатике

Написание компьютерных программ и их верификация.

При проектировании вычислительных устройств используется как теоретический инструмент.

Использование логических операций в электронных микросхемах в качестве базовых.

Логический подход к представлению и решению различных практических задач с использованием вычислительной техники.

Основные понятия логики

• Понятие — форма мышления, в которой отражаются существенные отличительные признаки предметов.  Понятие имеет две основные логические характеристики: содержание и объем
• Высказывание (суждение) — форма мышления, в которой что-либо утверждается или отрицается о предметах, их свойствах, или отношениях.  Высказывание характеризуется своим содержанием и формой.
• Умозаключение — форма мышления, посредством которой из одного или нескольких высказываний, называемых посылками, мы по определенным правилам вывода получаем заключение.

Логические операции

• Инверсия — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда исходное высказывание ложно. В выражениях обозначается ¬A или A. Читается «НЕ» (например, «не А»). Конъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания. В выражениях обозначается A ∧ B или A & B (знак может не указываться — AB). Читается «И» (например, «А и Б») Дизъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда, когда истинно хотя бы одно из исходных высказываний. В выражениях обозначается A ∨ B, иногда A + B. Читается «ИЛИ» (например, «А или Б») Импликация — это логическая операция, образующая сложное высказывание, ложное тогда и только тогда, когда первое исходное высказывание истинно, а второе — ложно. В выражениях обозначается A ⇒ B или A → B. Читается «ЕСЛИ...ТО» (например, «если А, то Б») Эквивалентность — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда значения исходных высказываний совпадают. В выражениях обозначается A ⇔ B или A ≡ B. Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)
• Инверсия — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда исходное высказывание ложно.
• В выражениях обозначается ¬A или A.
• Читается «НЕ» (например, «не А»).
• Конъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания.
• В выражениях обозначается A ∧ B или A & B (знак может не указываться — AB).
• Читается «И» (например, «А и Б»)
• Дизъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда, когда истинно хотя бы одно из исходных высказываний.
• В выражениях обозначается A ∨ B, иногда A + B.
• Читается «ИЛИ» (например, «А или Б»)
• Импликация — это логическая операция, образующая сложное высказывание, ложное тогда и только тогда, когда первое исходное высказывание истинно, а второе — ложно.
• В выражениях обозначается A ⇒ B или A → B.
• Читается «ЕСЛИ...ТО» (например, «если А, то Б»)
• Эквивалентность — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда значения исходных высказываний совпадают.
• В выражениях обозначается A ⇔ B или A ≡ B.
• Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)

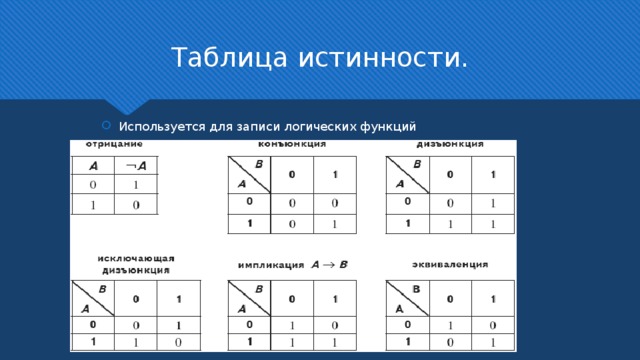
Таблица истинности.

• Используется для записи логических функций

Законы логики

• Закон исключенного третьего
• Высказывание может быть либо ложным, либо истинным. Третьего не дано.
• A ∨ ¬A = 1

• Закон непротиворечия
• Высказывание не может противоречить самому себе.
• A ∧ ¬A = 0

• Закон двойного отрицания
• Если дважды отрицать высказывание, то получится исходное.
• ¬¬A = A

• Законы повторения (идемпотентности)
• Сколько ни повторяй, значение не изменится.
• A∨A = A | A∧A = A

• Законы коммутативности (переместительные)
• От перестановки высказываний значение не изменится.
• A∨B = B∨A | A∧B = B∧A

Законы логики

• Законы ассоциативности (сочетательные)
• От порядка выполнения операций конъюнкции (дизъюнкции) значение не изменится.
• (A∨B)∨C = A∨(B∨C) | (A∧B)∧C = A∧(B∧C)

• Законы дистрибутивности (распределительные)
• A∨(B∧C) = (A∨B)∧(A∨C)
• A∧(B∨C) = (A∧B)∨(A∧C)

• Законы поглощения
• A∨(A∧B) = A | A∧(A∨B) = A

• Законы де Моргана
• ¬(A∧B) = ¬A ∨ ¬B | ¬(A∨B) = ¬A ∧ ¬B

• Свойства констант
• (Это, строго говоря, не отдельные законы, а непосредственные следствия из определений операций. )
• A ∧ 0 = 0 | A ∨ 0 = A
• A ∧ 1 = A | A ∨ 1 = 1

Обозначения логических операций

Логическая связка

Название логической операции

не

Обозначения

Отрицание, инверсия

и, а, но

Конъюнкция, логическое умножение

Ø, ù

или

если ..., то

&, • ,  Ù

Дизъюнкция, логическое сложение

Импликация, следование

V, +

тогда и только тогда, когда

Þ,®

эквивалентность, эквиваленция, равнозначность

Û, ~, º, «

Использование

• Логические основы компьютера
• В ЭВМ используются различные устройства, работу которых прекрасно описывает алгебра логики. К таким устройствам относятся группы переключателей, триггеры, сумматоры.
• Кроме того, связь между булевой алгеброй и компьютерами лежит и в используемой в ЭВМ системе счисления. Как известно она двоичная. Поэтому в устройствах компьютера можно хранить и преобразовывать как числа, так и значения логических переменных.
• Переключательные схемы
• В ЭВМ применяются электрические схемы, состоящие из множества переключателей. Переключатель может находиться только в двух состояниях: замкнутом и разомкнутом. В первом случае – ток проходит, во втором – нет. Описывать работу таких схем очень удобно с помощью алгебры логики. В зависимости от положения переключателей можно получить или не получить сигналы на выходах.
• Вентили, триггеры и сумматоры
• Вентиль представляет собой логический элемент, который принимает одни двоичные значения и выдает другие в зависимости от своей реализации. Так, например, есть вентили, реализующие логическое умножение (конъюнкцию), сложение (дизъюнкцию) и отрицание.
• Триггеры и сумматоры – это относительно сложные устройства, состоящие из более простых элементов – вентилей.
• Триггер способен хранить один двоичный разряд, за счет того, что может находиться в двух устойчивых состояниях. В основном триггеры используется в регистрах процессора.
• Сумматоры широко используются в арифметико-логических устройствах (АЛУ) процессора и выполняют суммирование двоичных разрядов.

Спасибо за внимание!