Логарифмические диковинки

Логарифмы – это рифмы,

Словно в музыке слова.

С ними проще вычисления –

Не сложней, чем дважды два.

Л. Нестерова

Логарифмические диковинки

Морозова Светлана Владимировна

Муниципальное бюджетное общеобразовательное учреждение

«Центр образования»

г. Череповца Вологодской области

Что такое логарифм?

Логарифмом данного числа по данному основанию называется показатель степени, в которую надо возвести это основание, чтобы получить данное число.

Слово «логарифм» происходит от греческих слов  - число и  - от ношение . Переводится как «от ношения чисел», одно из кот орых являет ся членом арифмет ической прогрессии, а другое –геомет рической.

Основное достоинство логарифмов – способность сводить сложные действия к простым на основании свойств логарифмов .

Логарифмы возникли в 16 веке в связи с необходимостью проведения большого объема приближенных вычислений в ходе решения практических задач.

С точки зрения вычислительной практики, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы нумерации.  

Изобретение логарифмов, сократив работу астронома, продлило ему жизнь. П.С.Лаплас

Джон Непер ( 1550-1617)

Генри Бриггс (1561-1631 )

Шотландский математик

Лондонский профессор

«Описание удивительной таблицы логарифмов».1614 г.

«Логарифмическая арифметика».1620 г.

5

5

В1619 г. лондонский учитель математики Джон Спайделл переиздал таблицы Непера, преобразованные так, что они фактически стали таблицами натуральных логарифмов Термин «натуральный логарифм» предложил итальянский математик Пьетро Менголи в середине XVI века.

6

6

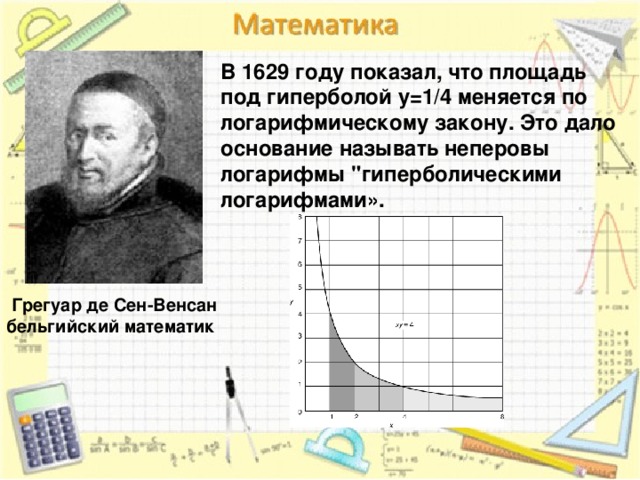
В 1629 году показал, что площадь под гиперболой y=1/4 меняется по логарифмическому закону. Это дало основание называть неперовы логарифмы "гиперболическими логарифмами».

Грегуар де Сен-Венсан

бельгийский математик

6

В 1747—1751годах Эйлером была опубликована полная теория логарифмов отрицательных и комплексных чисел и по существу ничем не отличается от современной.

е = 2,718 28...

е = 2,718 28...

Леона́рд Э́йлер

(1707-1783)

швейцарский, немецкий и российский математик и механик

6

Логарифмическая линейка.

Подобная шкала используется во многих областях науки, например:

-Физика — интенсивность звука (децибелы). Формула зависимости: N ~ lg S, где N - величина громкости, S - сила звука.

-Астрономия — шкала яркости звёзд.

-Химия — активность водородных ионов (pH).

-Сейсмология — шкала Рихтера.

-Теория музыки — нотная шкала, по отношению к частотам нотных звуков.

-История — логарифмическая шкала времени.

6

Десятичный логарифм

Натуральный логарифм - логарифм, основание которого - число Эйлера е = 2,718 28... Натуральный логарифм числа а обозначают ln а .

- логарифм по основанию 10. Десятичный логарифм числа а обозначают lg а .

Двоичный логарифм - логарифм по основанию 2. Они применяются в теории информации, информатике. Двоичный логарифм числа а обозначают log 2 a

Джон Непер ( 1550-1617)

10

10

  Логарифмическая спираль

Спираль называется логарифмической, т.к. логарифм расстояния (log r) возрастает пропорционально углу поворота ф.

а

Декарт.

10

“… моей навязчивой идеей, настоящей маниакальной страстью, стала картина Я. Вермера “Кружевница”, репродукция которой висела в отцовском кабинете”

Сальвадор Дали

«Кружевница», Ян Вермер

12

  Логарифмические спирали:

-в природе

-у человека

13

13

В мире нет ничего, кроме Красоты.

В Красоте нет ничего, кроме Формы.

В Форме нет ничего, кроме пропорций.

В пропорциях нет ничего, кроме Числа.

Пифагор.

Нумерология

«Золотые» логарифмы – это логарифмы с основанием равным числу Ф (1, 6180339) описываются формулой

log Ф M = P

Три основания логарифмов:

10,000 ; 3,838 ; 2,71 .

14

14

Тихий шелест листьев оценивается в 1 бел

Громкость шума, выраженная в белах, равна десятичному логарифму его физической силы.

15

Рассмотрим пример – «игра на рояле». Номера клавишей рояля представляют собой логарифмы чисел колебаний соответствующих звуков; номер октавы представляет собой характеристику, а номер звука в данной октаве мантиссу этого логарифма.

16

  По логарифмической спирали закручены многие галактики.

По логарифмической спирали формируется и тело циклона

17

Логарифмы в биологии

Задача В начальный момент времени было 8 бактерий, через 2 ч после помещения бактерий в питательную среду их число возросло до 100. Через сколько времени с момента помещения в питательную среду следует ожидать колонию в 500 бактерий? Решение. q=8, t=2, p=100/8, B=500. Значит, требуемое время соответствует значению выражения

то есть примерно через 3 ч. 15 мин

17

Логарифмы в биофизике

Водородный показатель, "pH" ,

 — это мера активности ионов водорода в растворе, количественно выражающая его кислотность,

вычисляется как

отрицательный десятичный логарифм концентрации водородных ионов ,

выраженной в молях на литр

17

Во-первых , логарифмы и сегодня позволяют упрощать вычисления.

Во-вторых , испокон веков целью математической науки было помочь людям узнать больше об окружающем мире, познать его закономерности и тайны.

Вывод : логарифмы – важные составляющие не только математики, но и всего окружающего мира, поэтому интерес к ним не ослабевает с годами и их необходимо изучать.

20