Решение простейших тригонометрических уравнений.
Уравнения вида sin x = a и cos x = a, где |а| ≤ 1, tg x = a и ctg x = a, где а ϵ R являються простейшими тригонометрическими уравнениями.
.sin x = a sin x = -a
arcsin(- a) = - arcsin a
x = (-1)k ∙arcsin a + πk, n є Z x = (-1)k+1 ∙arcsin a + πk, n є Z
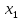 = arcsin a + 2πk, n є Z
= arcsin a + 2πk, n є Z 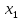 = -arcsin a + πk, n є Z
= -arcsin a + πk, n є Z
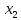 =π -arcsin a + 2πk, n є Zπ
=π -arcsin a + 2πk, n є Zπ 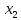 = -(π-arcsin a )+ πk, n є Z
= -(π-arcsin a )+ πk, n є Z
cos x = a cos x =- a
arcсos(- a) =(π-arccos a)
x = ± arccos a + 2πn, n є Z x = ± (π-arccos a)+ 2πn, n є Z
tg x = a tg x =-a
x = arctg a + πn, n є Z x = -arctg a + πn, n є Z
ctg x = a ctg x = a
x = arcctg a + πn, n є Z. x =-arcctg a + πn, n є Z.
Пример:
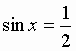
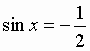
Решение:
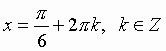
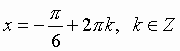
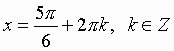
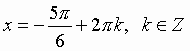
Пример:
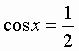
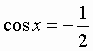
Решение:
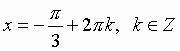
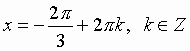
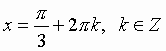
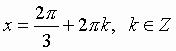
Пример
![]()
![]()
![]()
![]()
Решение:
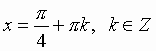
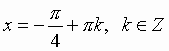
Частные случаи:
![]()
![]()
![]()
![]()
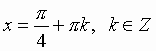
![]()
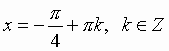

 Получите свидетельство
Получите свидетельство Вход
Вход












 Лекция- решение простейших тригонометрических уравнений (90.3 KB)
Лекция- решение простейших тригонометрических уравнений (90.3 KB)
 0
0 505
505 39
39 Нравится
0
Нравится
0


