Лекция № 1
Тема. Функция и ее свойства. Предел функции.
Цели:
обобщить и расширить знания студентов о функции и свойствах числовой функции; формировать умение анализировать функцию; совершенствовать умение вычислять значение функции в точке, находить область определения и множество значений функции; способствовать формированию навыка нахождения предела функции.
продолжить развитие способностей к аналитическому и алгебраическому мышлению.
продолжить воспитание у студентов познавательного интереса к математике, ответственности, чувства долга, академической самостоятельности.
Ход занятия
Организационный момент
Актуализация знаний
В математике одним из важных понятий является понятие функции. Как вы понимаете это слово? (ответы студентов)
Каким образом можно задать функцию? (ответы студентов)
Изучение нового материала
В своей практической деятельности человек сталкивается с величинами различной природы: длина, площадь, объем, масса, температура, вес и т.д.
В зависимости от конкретных условий некоторые из этих величин принимают одно и то же постоянное значение, т.е. не меняются; другие наоборот, принимают различные значения.
Все величины, изучаемые в математике, делятся на постоянные и переменные. Те из величин, которые в рассматриваемом процессе ![]() называются
называются ![]() величинами.
величинами.
| ВЕЛИЧИНЫ | |||
| Постоянные | Переменные | ||
| Абсолютно постоянные | Параметры | Независимые | Зависимые |
| В 1 часе 60 минут | 3 и 5 - параметры | х | у |
|
| у=3х+5 | ||
Определение. Правило, или закономерность, при котором каждому значению х соответствует единственное значение у, называется функцией. Обозначение: ![]() .
.
Аргумент х – независимая переменная х.
Значение функции f(x) – число у, соответствующее значению х.
Область определения D(f) – множество возможных значений переменной х.
Множество значений E(f) – множество, состоящее из всех значений функции f(x).
Выражение у=х+5 является функцией, т.к. каждому значению аргумента х соответствует единственное значение функции у.
Область определения: (-;+). Область значений: (-;+).
Функция определена во всех точках области определения. Такую функцию называют непрерывной. у=х+5 – непрерывная функция.
у(0)=5, у(1)=6, у(2)=7, у(-1)=4.
А теперь посмотрим как ведет себя эта функция у=х+5 вблизи точки х=1:
у(0,01)=5,01
у(0,02)=5,02
у(0,1)=5,1
у(0,5)=5,5
у(0,9)=5,9
у(0,99)=5,99
Итак, при х 1 у6. Говорят, что у=6 является пределом функции у=х+5 при х 1. Записывают: ![]()
Р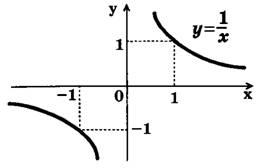 ассмотрим другую функцию: у=
ассмотрим другую функцию: у=![]()
Функция у=![]() неопределенна в точке х=0, т.к. на 0 делить нельзя. Значит функция у=
неопределенна в точке х=0, т.к. на 0 делить нельзя. Значит функция у=![]() не является непрерывной. Точку х=0 называют точкой разрыва функции у=
не является непрерывной. Точку х=0 называют точкой разрыва функции у=![]() .
.
График функции у=![]() - гипербола. График функции у=
- гипербола. График функции у=![]() не пересекает ось Оу, но при неограниченном приближении х к нулю ветви гиперболы неограниченно приближаются к оси Оу. При неограниченном увеличении х ветви гиперболы неограниченно приближаются к оси Ох, нигде ее не пересекая.
не пересекает ось Оу, но при неограниченном приближении х к нулю ветви гиперболы неограниченно приближаются к оси Оу. При неограниченном увеличении х ветви гиперболы неограниченно приближаются к оси Ох, нигде ее не пересекая.
На графике видно, что при х+ или х-, у0. Значит ![]()
Простейшие пределы
Любой предел состоит из трех частей:
Всем известного значка предела lim.
Записи под значком предела, в данном случае x1. Запись читается «икс стремится к единице». Чаще всего – именно x, хотя вместо x на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность .
Функции под знаком предела, в данном случае ![]() .
.
Сама запись
![]()
читается так: «предел функции ![]() при икс стремящемся к единице».
при икс стремящемся к единице».
Выражение «икс стремится к единице» следует понимать так: х последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Чтобы решить вышерассмотренный пример нужно просто подставить единицу в функцию, стоящую под знаком предела:
![]()
![]()
Что означает х? Это значит, что х неограниченно возрастает, то есть: сначала х=10, потом х=100, потом х=1000, затем х=100000 и так далее до бесконечности.
А что в это время происходит с функцией 1-х?
1-10=-9; 1-100=-99; 1-1000=-999; ….
Итак: если х, то функция 1-х стремится к минус бесконечности: ![]()
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию 1-х бесконечность и получаем ответ.
![]()
Снова начинаем увеличивать х до бесконечности и смотрим на поведение функции:
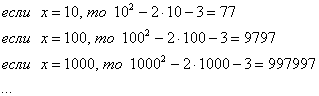
Вывод: при х функция х2-2х-3 неограниченно возрастает: ![]()
Попытайтесь самостоятельно проанализировать нижеследующее и запомните простейшие виды пределов:
![]()
![]()
![]()
![]()
Обратите внимание на следующее: даже если дан предел с большим числом в числителе, да хоть с миллионом: , то все равно , так как рано или поздно х начнёт принимать такие гигантские значения, что миллион по сравнению с ними будет ничтожно мал.
П одставляем 0 в функцию . Получаем:
Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число. Тогда
Запомните: если конечное положительное число (любое, даже очень маленькое, как 0,0001) разделить на бесконечно малое число х0, то получится .
Закрепление новых знаний.
| Задание 1 | Задание 2 | Задание 3 | Задание 4 | ||||
| |
| |
| |
| |
|
| |
| |
| |
| |
|
| |
| |
| |
| |
|
| |
| |
| |
| |
|
5. Подведение итогов занятия.
6. Домашнее задание.
Найдите пределы:
|
|
|
|
|
|
|
|
7. Литература:
Математика для техникумов- И.И. Валуцэ, Г.Д. Дилигул, Москва, 1980
Данко П.Е. Высшая математика в упражнениях и задачах: В 2т. учеб. пособ.
4

 Получите свидетельство
Получите свидетельство Вход
Вход












 Лекция по теме: "Функция и ее свойства. Предел функции" (153 KB)
Лекция по теме: "Функция и ее свойства. Предел функции" (153 KB)
 0
0 132
132 2
2 Нравится
0
Нравится
0


