Составитель: Сурядная Инна
Лабораторная работа по теме «Применение производной для исследования монотонности и экстремумов функции».
Тема: Применение производной для исследования монотонности и экстремумов функции
Цель: познакомиться с теоремами, показывающими, как по знаку производной можно установить характер монотонности функции на промежутке.
Ход работы:
I. Формулирование гипотезы.
Производная функции и свойства функции (монотонность и экстремумы функции) связаны между собой.
II. Проведение опыта. Монотонность функции.
1. Откройте приложение GeoGebra.
2. Постройте два разных графика функции  .
.
Вспомните от чего зависит вид такого графика. _____________________________________.
3. Постройте графики производных функций из пункта 2. Для этого откройте список команд, найдите раздел «Функции и исчисления». Затем нажмите Производная [ ].
4. Проанализируете промежутки возрастания и убывания функций и значения производных данных функций на промежутках. Данные занесите в таблицу 1 и таблицу 2.
Таблица 1. Данные
| Функция | Промежутки возрастания | Промежутки убывания | Знак производной (
|
| | | | |
| | | | |
Таблица 2. Сравнение
| Знак производной | Вывод | Промежутки |
|
| Следует | Промежутки возрастания |
|
| Следует | Промежутки убывания |
III. Вывод.
Сформулируете полученные выводы о связи между характером монотонности функции и знаком её производной.
1) Если во всех точках открытого промежутка 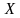 выполняется неравенство
выполняется неравенство 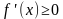 (причём равенство
(причём равенство 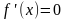 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция
выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция 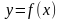 _____________ на промежутке
_____________ на промежутке 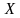 .
.
2) Если во всех точках открытого промежутка X выполняется неравенство 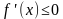 (причём равенство
(причём равенство 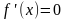 выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция
выполняется лишь в отдельных точках и не выполняется ни на каком сплошном промежутке), то функция 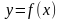 ______________ на промежутке
______________ на промежутке 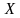 .
.
IV. Проведение опыта. Экстремумы функции.
1. Откройте приложение GeoGebra.
2. Постройте два разных графика функции 
3. Постройте графики производных функций из пункта 2. Для этого откройте список команд, найдите раздел «функции и исчисления». Затем нажмите Производная[ ].
4. Проанализируете экстремумы функций и значения производных данных функций на промежутках. Данные занесите в таблицу 3.
Таблица 3. Функция 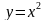
| Промежутки | | |
| Знак производной | | |
| Поведение функции на промежутках | | |
| Точка экстремума | | |
Таблица 4. Функция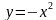
| Промежутки | | |
| Знак производной | | |
| Поведение функции | | |
| Точка экстремума | | |
V. Вывод.
Сформулируете полученные выводы о связи между экстремумами функции и знаком её производной.
1) В точке 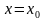 производная меняет знак с положительного на отрицательный, значит,
производная меняет знак с положительного на отрицательный, значит, 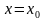 — точка максимума функции
— точка максимума функции 
2) В точке 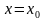 она меняет знак с отрицательного на положительный, значит,
она меняет знак с отрицательного на положительный, значит, 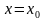 — точка минимума функции
— точка минимума функции 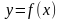 ;
;
3) если у этой точки существует такая окрестность, что в ней и слева, и справа от точки  знаки производной одинаковы, то в точке
знаки производной одинаковы, то в точке  экстремума ___________________.
экстремума ___________________.
VI. Выводы:
1. Чтобы исследовать функцию на монотонность и экстремумы, необязательно строить график производной, достаточно определить знаки ______________ на промежутках, на которые ________________ и _______________ точки разбивают область определения функции.
2.
1) f'(x)≥0, то функция в нём не убывает;
2) f'(x)≤0, то функция в нём не возрастает;
3) f'(x)0, то функция в нём возрастает;
4) f'(x), то функция в нём убывает.
3. Если функция 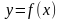 имеет ____________ в точке
имеет ____________ в точке 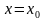 , то в этой точке производная функции либо равна нулю, либо не существует.
, то в этой точке производная функции либо равна нулю, либо не существует.
Пусть функция 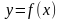 непрерывна на промежутке
непрерывна на промежутке 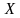 и имеет внутри промежутка стационарную или критическую точку
и имеет внутри промежутка стационарную или критическую точку 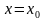 .
.
Тогда:
1) В точке 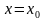 производная меняет знак с положительного на отрицательный, значит,
производная меняет знак с положительного на отрицательный, значит, 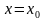 — точка ______________ функции
— точка ______________ функции 
2) В точке 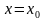 производная меняет знак с отрицательного на положительный, значит,
производная меняет знак с отрицательного на положительный, значит, 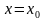 — точка ______________ _ функции
— точка ______________ _ функции 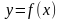 ;
;
3) если у этой точки существует такая окрестность, что в ней и слева, и справа от точки  знаки производной одинаковы, то в точке
знаки производной одинаковы, то в точке  экстремума ___________________.
экстремума ___________________.

 Получите свидетельство
Получите свидетельство Вход
Вход


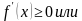

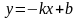









 Лабораторная работа (19 KB)
Лабораторная работа (19 KB)
 0
0 281
281 4
4 Нравится
0
Нравится
0



