Квадратный трехчлен

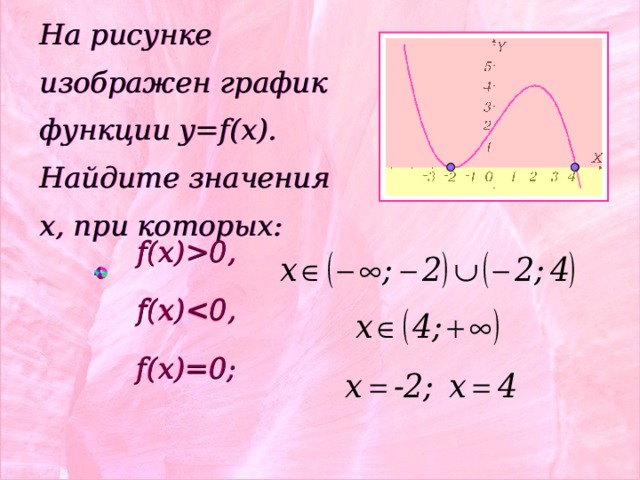
На рисунке изображен график функции y=f(x). Найдите значения x, при которых:

функция

возрастает,

убывает;

функция

возрастает,

убывает;

На рисунке изображен график функции y=f(x). Найдите значения x, при которых:

функция на отрезке [-3;3] принимает

наибольшее значение, наименьшее значение.

функция на отрезке [-3;3] принимает

наибольшее значение, наименьшее значение.

ТЕМА

КВАДРАТНЫЙ

ТРЁХЧЛЕН

И ЕГО КОРНИ

ОПРЕДЕЛЕНИЕ

Квадратным трёхчленом называется многочлен вида

ax 2 + bx + c,

где x – переменная, a, b и c - некоторые числа, причем a  0.

Значение квадратного трёхчлена

Значение квадратного трёхчлена

3x 2 – 2x – 5 зависит от значения x.

Например:

Если x=5, то 3x 2 – 2x – 5 = 60;

Если x=1, то 3x 2 – 2x – 5 = -4;

Если x=-1, то 3x 2 – 2x – 5 = 0;

Число -1 является корнем этого трёхчлена.

Корень квадратного трёхчлена

Корнем квадратного трёхчлена называется значение переменной, при котором значение этого трёхчлена равно нулю.

Например:

Если x=-1, то 3x 2 – 2x – 5 = 0;

Число -1 является корнем трёхчлена 3x 2 – 2x – 5 .

Пример №3

• Доказать, что из всех прямоугольников с периметром 20 см наибольшую площадь имеет квадрат.

Решение.

20 : 2 = 10 см - полупериметр

x см

(10 – x) см

Тогда x(10 – x) см 2 – площадь прямоугольника.

• Раскроем скобки и преобразуем это выражение, выделив квадрат двучлена:

Решение.

x(10 – x) =

10x – x 2 =

– x 2 +10x =

-(x 2 -10x) =

-(x 2 + 2 · (-5) · x + 25 – 25)

= -((x-5) 2 – 25) =

-(x-5) 2 + 25.

Решение.

-(x-5) 2 + 25.

Первое слагаемое всегда меньше или равно нулю, значит, наибольшее значение, которое оно принимает равно нулю, а это возможно при x=5.

Решение.

-(x-5) 2 + 25.

Т.о. прямоугольник имеет наибольшую площадь при x=5; тогда и вторая сторона равна 10 – 5 =5, а это квадрат.

Урок № 6

Является ли число

Является ли число

корнем квадратного трехчлена?

корнем квадратного трехчлена?

Имеет ли квадратный трехчлен корни, и если имеет, то сколько?

Имеет ли квадратный трехчлен корни, и если имеет, то сколько?

1

2

2

Представьте выражение в виде квадрата двучлена:

=

=

=

Математический диктант

• 1) f(x) = x 2 – 3x + 1;

Найдите f(0); f(-1); f( ).

• 2) f(x) = x 2 -3x

При каком значении x f(x) = 0?

• 3) Приведите пример линейной возрастающей функции.
• 4) Функция y = f(x) – убывающая. Сравните f(3) и f(5).
• 5) Начертите график какой – нибудь функции возрастающей при x  [-3;1]  [3;5] и убывающей при x  [1;3]

f(5). 5) " width="640"

Ответы.

• 1)1; 5;

• 2) x(x-3)=0; Ответ: 0;3.
• 3) y = 2x + 3;
• 4) f(3) f(5).
• 5)

Разложение квадратного трехчлена на множители.

Урок №7

Математический диктант

• 1) f(x) = x 2 – 4x;

Найдите f(0); f(-1); f( ).

• 2) f(x) = x 2 -4x

При каком значении x f(x) = 0?

• 3) Приведите пример линейной убывающей функции.
• 4) Функция y = f(x) –возрастающая. Сравните f(1) и f(3).
• 5) Начертите график какой – нибудь функции убывающей при x  [ -3;1]  [3;5] и возрастающей при x  [1;3]

Ответы.

• 1)0; 5;

• 2) x(x-4)=0; Ответ: 0;4.
• 3) y = -2x + 3;
• 4) f(1)
• 5)

Разложите на множители многочлен:

Сократите дробь:

т еорема

Если x 1 и x 2 – корни квадратного

трёхчлена ax 2 + bx + c, то

ax 2 + bx + c = a (x – x 1 )(x – x 2 ).

Замечание

Если квадратный

трёхчлен не имеет корней , то

его нельзя разложить на множители, являющиеся многочленами первой степени.