Квадратные корни

• Действительные числа
• Действительные числа

• Рациональные числа
• Иррациональные числа.

2. Арифметический квадратный корень

• Квадратные корни. Арифметический квадратный корень.
• Уравнение х 2 =а.
• Функция y= и ее график.

3. Свойства арифметического квадратного корня.

• Квадратный корень из произведения и степени.
• Квадратный корень из степени.

4. Применение свойств арифметического квадратного корня

• Вынесение множителя из-под знака корня. Внесение множителя под знак корня.
• Преобразование выражений, содержащих квадратные корни.

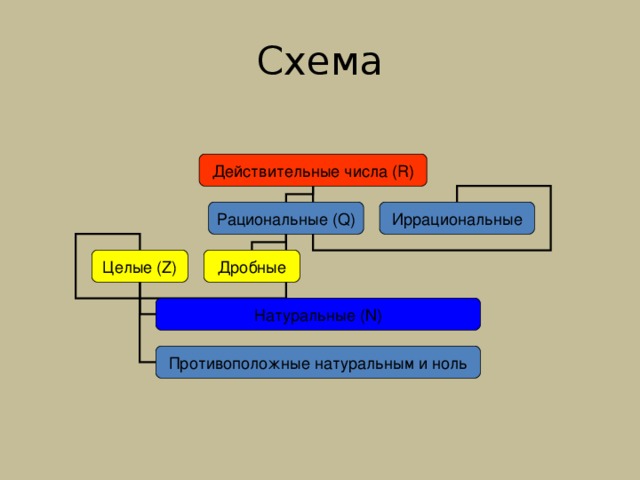
Действительные числа ( R)

Рациональные (Q)

Целые (Z)

Натуральные (N)

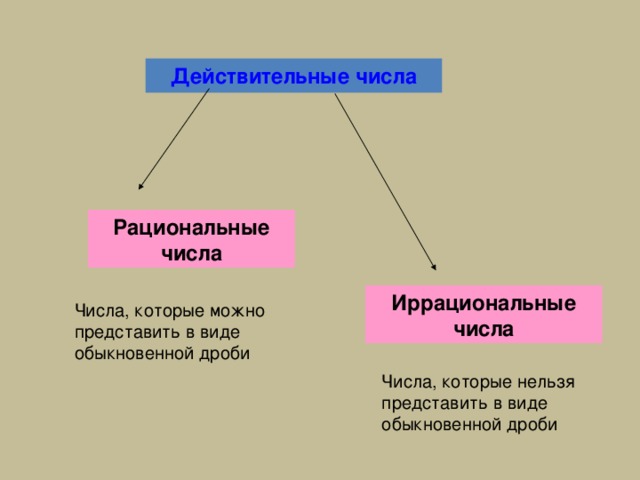
Действительные числа

Рациональные числа

Иррациональные числа

Числа, которые можно представить в виде обыкновенной дроби

Числа, которые нельзя представить в виде обыкновенной дроби

Множество натуральных чисел обозначают

N : 1, 2, 3, 4, ...

Это числа, употребляемые при счете предметов.

Например, 10

- 3

Множество целых чисел обозначают Z :

...-3, -2, -1, 0, 1, 2, 3,...

Это числа натуральные, противоположные им и ноль .

Например, -15

23.5

Множество рациональных чисел обозначают Q .

Это целые числа и дробные.

5.8

Действительные числа обозначают R

Это рациональные и иррациональные числа

Всякое рациональное число можно представить в виде дроби

Где m - целое число, а n - натуральное.

Например:

0. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а. Обозначается . " width="640"

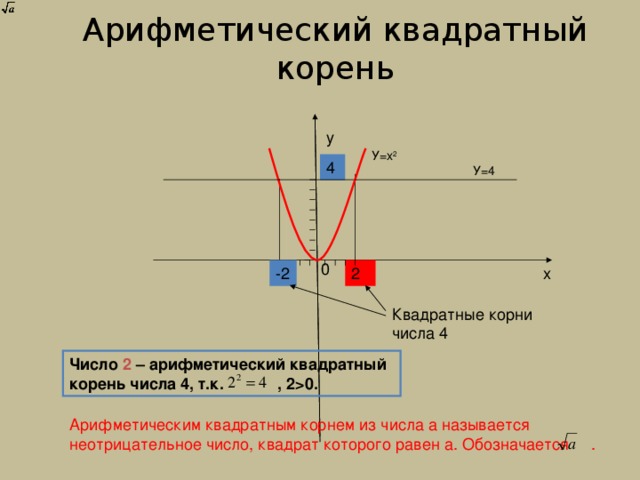
Арифметический квадратный корень

У=х 2

У=4

Число 2 – арифметический квадратный корень числа 4, т.к. , 2 0.

Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а. Обозначается .

0 уравнение имеет два корня. Если а=0 уравнение имеет один корень Например, х 2 =81 х=9 или х=-9 Х 2 =-25 Не имеет корней Х 2 =0 Х=0 " width="640"

Уравнение х 2 =а

Е сли а

Если а 0 уравнение имеет два корня.

Если а=0 уравнение имеет один корень

Например, х 2 =81

х=9 или х=-9

Х 2 =-25

Не имеет корней

Х 2 =0

Х=0

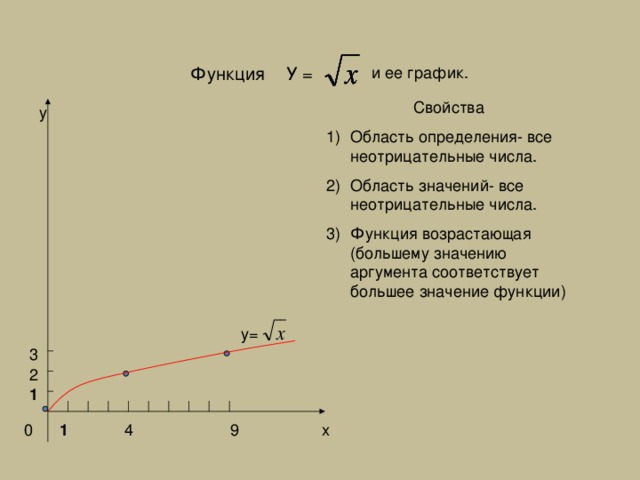
У =

Функция

у=

1

1

0, то " width="640"

Свойства квадратного корня

1)Квадратный корень из произведения и степени

Корень из произведения неотрицательных множителей равен произведению корней из этих множителей.

Если а 0, в 0, то

Применение свойств арифметического квадратного корня

Преобразование выражений, содержащих квадратные корни:

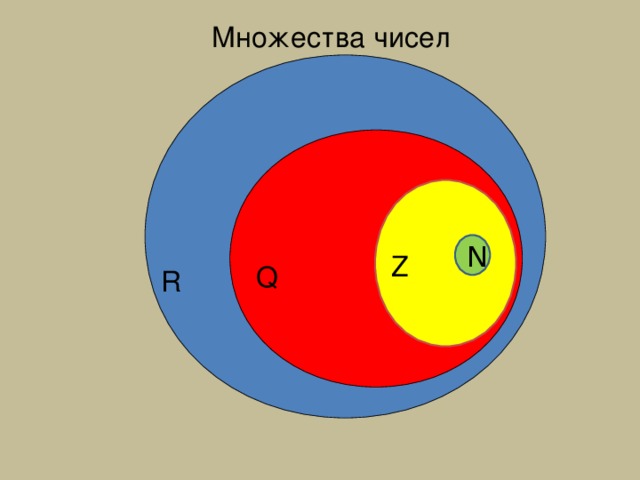
Множества чисел

N

Z

Q

R