Курсовая работа по теме "Разложение многочлена на множители"

МБОУ СОЛЕРУДНИКОВСКАЯ ГИМНАЗИЯ

КУРСОВАЯ РАБОТА

«Разложение многочлена на множители»

Выполнила:

Жаровская Ксения Витальевна,

Ученица 10 класса

физико-математического профиля

Руководитель:

учитель математики,

Хадачинская Нина Васильевна

п. Тыреть 2017

Введение 3

Основная часть 4

1.Вынесение общего множителя за скобки……………………………………………………...4

2.Способ группировки…………………………………………………………………………….4

3.Использование формул сокращенного умножения…………………………………………...5

4.Метод неопределенных коэффициентов………………………………………………………5

5.Разложение на множители квадратного трехчлена…………………………………………...6

6.Схема Горнера…………………………………………………………………………………...6

7.Способ замены переменной при разложении многочлена на множители…………………..9

8.Теорема Безу……………………………………………………………………………………9

Источники информации 12

Приложение 13

В результате изучения учебной программы 7-9 классов учениками приобретаются навыки разложения многочлена на множители способами:

1. Вынесение общего множителя за скобки;

2. Использование формул сокращенного умножения;

3. Способом группировки;

4. Разложение квадратного трехчлена на множители;

5. Способом выделения полного квадрата

С приближением единого государственного экзамена у учащихся порой возникают сложности с упрощением выражений. Основной частью данного задания является разложение многочленов на множители, что не всегда удается сделать теми способами, которыми мы изучаем в школе.

Следовательно, целью работы является обобщение и систематизация знаний по данной теме.

Цель:

Найти различные способы разложения многочлена на множители и выбрать из всех способов более универсальный.

Задачи:

1. Изучить литературу по данной теме

2. Найти способы разложения многочлена на множители, которые не изучаются в школьной программе.

3. Подробнее разобрать схему Гонера

4. Выступить с докладом перед учениками 10 класса

Что же тогда такое разложение на множители?

Тождественное преобразование, приводящее к произведению нескольких множителей - многочленов или одночленов, называют разложением многочлена на множители. В этом случае говорят, что многочлен делится на каждый из этих множителей.

Существует множество способ разложения многочлена на множители, рассмотрим некоторые из них:

1. Вынесение общего множителя за скобки

Вынесение общего множителя за скобки. Это преобразование является непосредственным следствием распределительного закона ac + bc = c(a + b)

Рассуждения из предыдущего пункта приводят нас к правилу вынесения за скобки общего множителя: нужно записать произведение общего множителя и скобок, содержащих исходную сумму, но без общего множителя.

Пример. Разложить многочлен на множители .

Решение. Имеем: .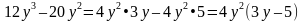

Ответ.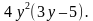

1. Способ группировки

Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения.

Пример. Разложить на множители многочлен .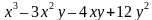

Решение. Сгруппируем слагаемые следующим образом:

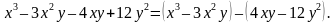
В первой группе вынесем за скобку общий множитель , а во второй − 4y . Получаем:

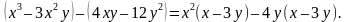Теперь общий множитель

(x–3y) также можно вынести за скобки:

x ² ( x – 3 y ) – 4 y ( x – 3 y ) = ( x – 3 y )( x ² – 4 y ). 

Ответ. (x–3y)(x ²–4y).

1. Использование формул сокращенного умножения

Очень часто приведение многочлена к стандартному виду можно осуществить путём применения формул сокращённого умножения . Все они доказываются непосредственным раскрытием скобок и приведением подобных слагаемых. Некоторые формулы сокращённого умножения нужно знать наизусть.

Пример. Упростите выражение ( ).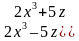

Решение. Воспользуемся формулой разности квадратов, получим: .

Ответ. .

Способ выделения полного квадрата

Способ выделения полного квадрата является одним из наиболее эффективных методов разложения на множители. Суть его состоит в выделении полного квадрата и последующего применения формулы разности квадратов.

Пример. Разложить на множители многочлен x ⁴ + 4 x ² – 1.

Решение. Имеем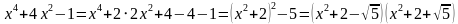

Ответ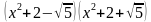

1. Метод неопределенных коэффициентов

Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной. Теоретической основой метода являются следующие утверждения.

Два многочлена равны тогда и только тогда, когда равны их коэффициенты.

Любой многочлен третьей степени имеет хотя бы один действительный корень, а потому разлагается в произведение линейного и квадратичного сомножителя.

Любой многочлен четвёртой степени разлагается в произведение многочленов второй степени.

Пример. Разложить на множители многочлен .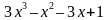

Решение. Поскольку многочлен третьей степени разлагается в произведение линейного и квадратичного сомножителей, то будем искать многочлены x – p и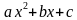

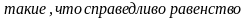
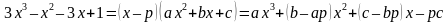. Приравнивая коэффициенты при одинаковых степенях в левой и правой частях этого равенства, получаем систему четырех уравнений для определения четырех неизвестных коэффициентов:

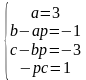
Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1. Итак, многочлен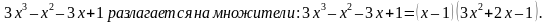

1. Разложение на множители квадратного трехчлена.

Квадратный трехчлен   раскладывается на два линейных множителя:  , где   и   являются корнями (комплексными или действительными).

Таким образом, разложение на множители квадратного трехчлена сводится к решению квадратного уравнения.

1. Схема Горнера.

Схема Горнера – это алгоритм деления (деление схемой Горнера) многочленов, записываемый для частного случая, если частное равно двучлену  .

Возьмём многочлен  , его коэффициенты:

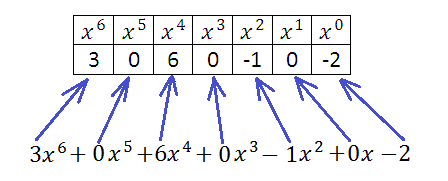
Каков же порядок заполнения нижней строки? Во-первых, у нее будет дополнительная ячейка слева, куда мы впишем корень многочлена, образующий бином, на который мы собираемся делить. Например, если делим на  , то корнем многочлена является число 2, если делим на  , то в эту ячейку впишем (-9). Пример: хотим разделить   на  , таблица изначально будет выглядеть так:

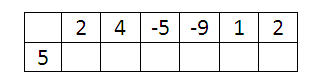
Степень полученного многочлена уменьшится на 1. Если сейчас мы начнем заполнять эту табличку, то под двойкой, которая была в делимом коэффициентом при пятой степени, окажется коэффициент при четвертой степени искомого частного, под 4 – коэффициент при кубе частного и т.д.

Так же просто заполнить вторую ячейку нижней строки: в нее просто вписывается число, стоящее в первой строчке:

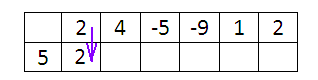
Рассмотрим дальнейшее заполнение таблицы на конкретном примере: разделим   на бином   (так как (-1) – это корень данного многочлена). Заполняем таблицу, пока только ту часть, которую умеем:вписываем коэффициенты в верхнюю строку, в дополнительную ячейку слева – корень (-1), в следующую переносим 1 из верхней строки: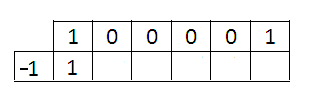

Чтобы заполнить следующую ячейку, берем корень, умножаем его на имеющийся коэффициент и прибавляем к полученному числу то, которое стоит над пустой ячейкой:

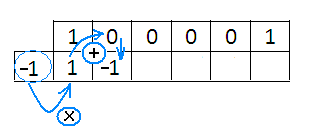
 Чтобы заполнить следующую, все повторяем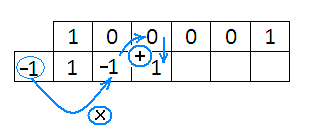

 И опять:

 И вот так закончится заполнение таблицы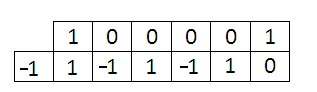

“Расшифровываем” ответ, при этом помним, что степень понизилась на 1:

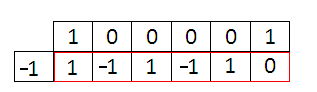
Ответ: 

Этот способ хорош своей быстротой и простотой. Им можно пользоваться и при делении с остатком: тогда в последней графе таблицы будет стоять не ноль, а этот самый остаток. Недостаток способа – неудобство деления в случае, если корень не целый, а представляет собой дробь.

Попробуем выполнить деление по схеме Горнера, если корень не целый, да еще и остаток есть. Поделим многочлен   на бином  . Заполняем таблицу:

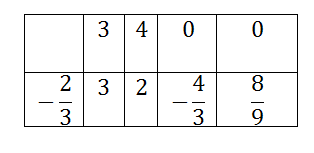
 Расшифруем ответ:

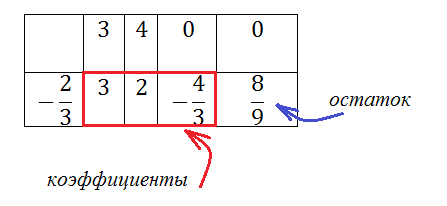
Итак, получилось следующее. При делении получился многочлен   и остаток  . Запишем это иначе:  .

1. Способ замены переменной при разложении многочлена на множители.

Часто замена переменной позволяет понизить степень многочлена и разложить его на множители.

Пример.

Разложить на множители  .

Решение.

Напрашивается замена  :

Корнями полученного квадратного трехчлена являются y=-2 и y=-3, поэтому,

Применяем формулу сокращенного умножения сумма кубов:

Так получили искомое разложение.

1. Теорема Безу.

Теорема Безу, невзирая на кажущуюся простоту и очевидность, является одной из базовых теорем теории многочленов. В данной теореме алгебраические характеристики многочленов (они позволяют работать с многочленами как с целыми числами) связываются с их функциональными характеристиками (которые позволяют рассматривать многочлены как функции).

Теорема Безу утверждает, что остаток от деления многочлена   на многочлен   - это   . Коэффициенты многочлена лежат в неком коммутативном кольце с единицей (к примеру, в поле вещественных либо комплексных чисел). Но наиболее важна не именно теорема, а следствие теоремы Безу: 

1. Число   - корень многочлена P(x) тогда и только тогда, когда P(x) делится без остатка на двучлен x-a.

Исходя из этого – множество корней многочлена P(x) тождественно множеству корней соответствующего уравнения x-a.

2. Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (когда старший коэффициент равен единице – все рациональные корни целые).

3. Предположим, что   - целый корень приведенного многочлена P(x) с целыми коэффициентами. Значит, для любого целого   число   делится на  . 

Теорема Безу дает возможность, найдя один корень многочлена, искать дальше корни многочлена, степень которого уже на 1 меньше: если  , то данный многочлен P(x) будет выглядеть так: 

Т.о., один корень найден и дальше находят уже корни многочлена  , степень которого на 1 меньше степени начального многочлена. Иногда таким методом - называется понижением степени - находят все корни данного многочлена.

 Теорема Безу примеры:

Найти остаток от деления многочлена   на двучлен  .

Теорема Безу примеры решения:

Исходя из теоремы Безу, искомый остаток соответствует значению многочлена в точке  . Тогда найдем  , для этого значение   подставляем в выражение для многочлена   вместо  . Получаем:

Ответ: Остаток = 5.

Сайты:

http://www.cleverstudents.ru

http://uztest.ru

Формулы для квадратов

Формулы для кубов

Формулы для четвёртой степени

Формулы для n-ой степени

где

МБОУ СОЛЕРУДНИКОВСКАЯ ГИМНАЗИЯ

Разложение многочлена на множители

Выполнила:

Жаровская Ксения Витальевна,

Ученица 10 класса

физико-математического профиля

  Руководитель:

учитель математики,

Хадачинская Нина Васильевна

п. Тыреть 2017

Введение

Цель

Задачи:

1.Изучить литературу по данной теме

Найти различные способы разложения многочлена на множители и выбрать из всех способов более универсальный

2.Найти способы разложения многочлена на множители, которые не изучаются в школьной программе.

3.Подробнее разобрать схему Гонера

4.Выступить с докладом перед учениками 10 класса

В результате изучения учебной программы 7-9 классов учениками приобретаются навыки разложения многочлена на множители способами:

1.Вынесение общего множителя за скобки;

2.Использование формул сокращенного умножения;

3.Способом группировки;

4.Разложение квадратного трехчлена на множители;

5.Способом выделения полного квадрата

С приближением единого государственного экзамена у учащихся порой возникают сложности с упрощением выражений. Основной частью данного задания является разложение многочленов на множители, что не всегда удается сделать теми способами, которыми мы изучаем в школе.

Вынесение общего множителя за скобки

Разложить многочлен на множители

Использование формул сокращенного умножения

Разложить на множители многочлен

Воспользуемся формулой разности квадратов, получим:

=

Способ группировки

Разложить на множители многочлен .

Сгруппируем слагаемые следующим образом:

В первой группе вынесем за скобку общий множитель

Теперь общий множитель также можно вынести за скобки:

Ответ. (x–3y)(x 2–4y).

Разложение на множители квадратного трехчлена.

Квадратный трехчлен   раскладывается на два линейных множителя:  , где являются корнями (комплексными или действительными).

Таким образом, разложение на множители квадратного трехчлена сводится к решению квадратного уравнения.

Способ выделения полного квадрата

Разложить на множители многочлен x 4 + 4 x 2 – 1.

Имеем

=

Cхема Горнера

Схема Горнера - это алгоритм вычисления значения многочлена при определенном значении переменной. Использование схемы Горнера значительно упрощает вычисления, а также помогает эффективно подбирать корни.

Разложить на множители многочлен x 3  – 5x 2  – 2x + 16.

Данный многочлен имеет целые коэффициенты. Если целое число является корнем этого многочлена, то оно является делителем числа 16. Таким образом, если у данного многочлена есть целые корни, то это могут быть только числа ±1; ±2; ±4; ±8; ±16. Степень многочлена, полученного в результате деления, всегда на 1 меньше, чем степень исходного.

2

1

− 5

1

− 2

− 3

16

− 8

0

Разделить 5 x 4 +5 x 3 + x 2 −11 на  x −1, используя схему Горнера.

Пример.

Докажем, что многочлен Р(х)=х 4 -6х 3 +7х-392

делится на х-7, и найдем частное от деления.

• Решение.

Используя схему Горнера, найдем Р(7):

Р(х)=(х-7)(х 3 +х 2 +7х+56).

7

1

1

-6

0

1

7

7

-392

56

0

• Основным преимуществом этого метода является компактность записи и возможность быстрого деления многочлена на двучлен. По сути, схема Горнера является другой формой записи метода группировки, хотя, в отличие от последнего, является совершенно ненаглядной

Источники информации

Сайты:

http://www.cleverstudents.ru

http://uztest.ru