Получите свидетельство
Вход
Специализированная гимназия № 8 с обучением на трех языках имени М.Х. Дулати
10 класс
Алгебра и начала анализа
Критические точки и
точки экстремума
функции
Л.С. Атанасян. Геометрия 10-11
учитель математики
Харченко Татьяна Викторовна
Шымкент-2020
Цель урока:
10.4.1.28
- знать определения критических точек и точек экстремума функции, условие существования экстремума функции.
Критерии оценивания
Учащийся:
Л.С. Атанасян. Геометрия 10-11
- Использует определение находит критические (стационарные) точки, используя определение;
- применяет необходимое и достаточное условие для определение точек экстремума функции.
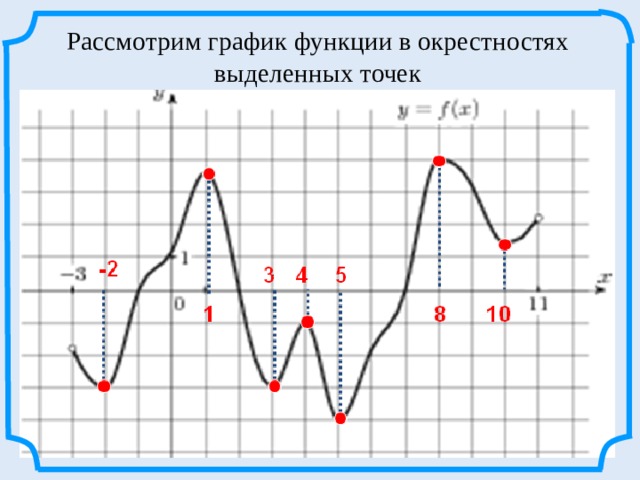
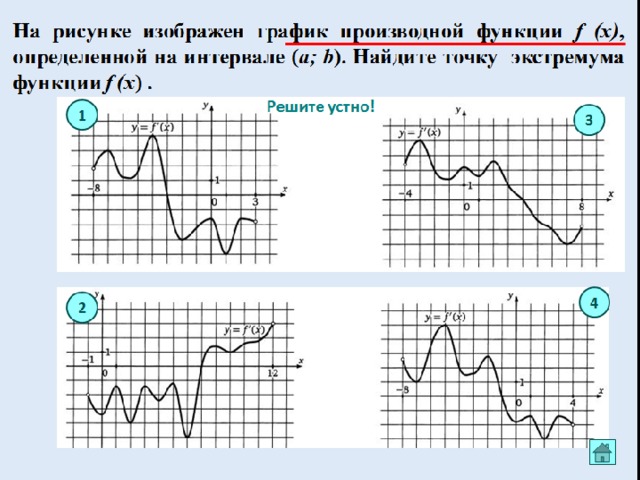
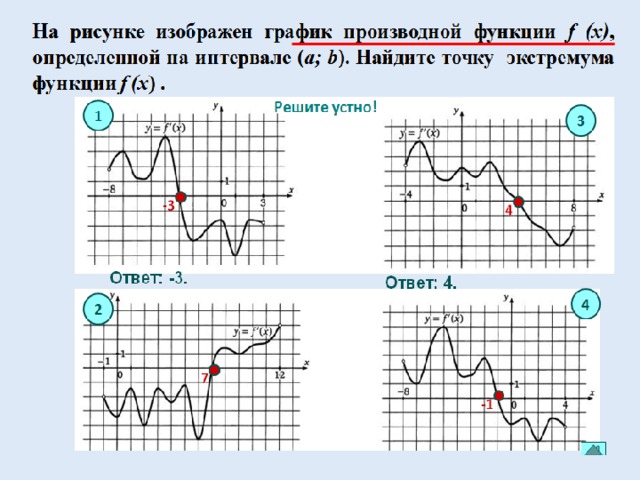
Рассмотрим график функции в окрестностях выделенных точек
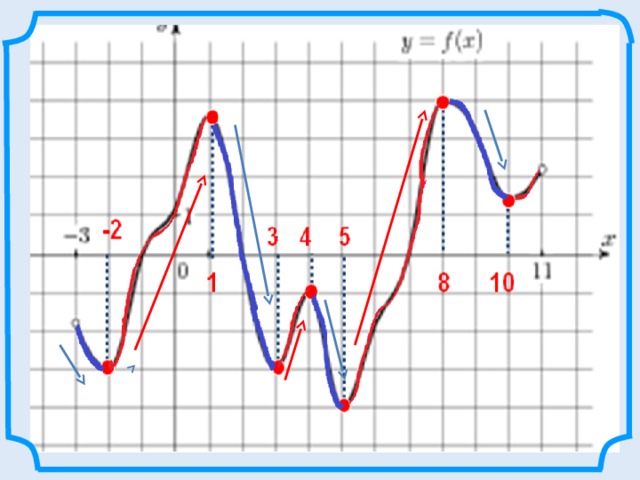
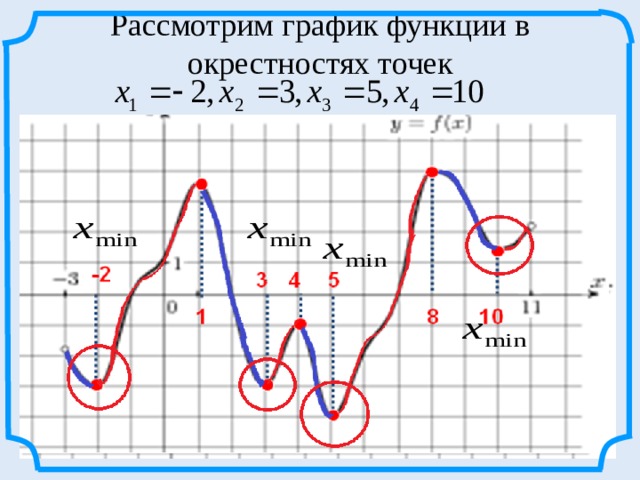
Рассмотрим график функции в окрестностях точек
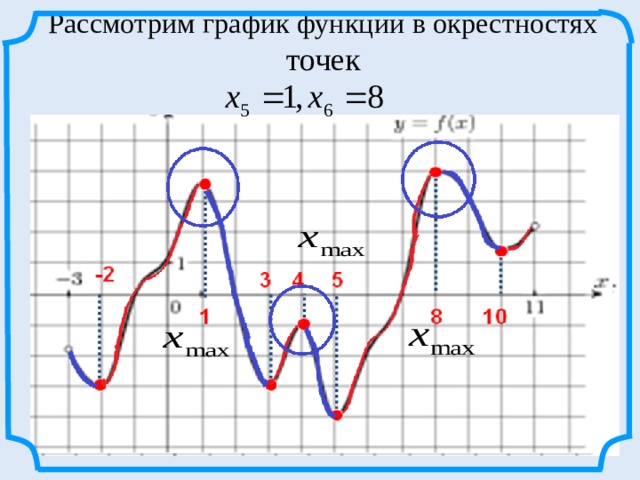
Рассмотрим график функции в окрестностях точек
f( х 0 ) " width="640"
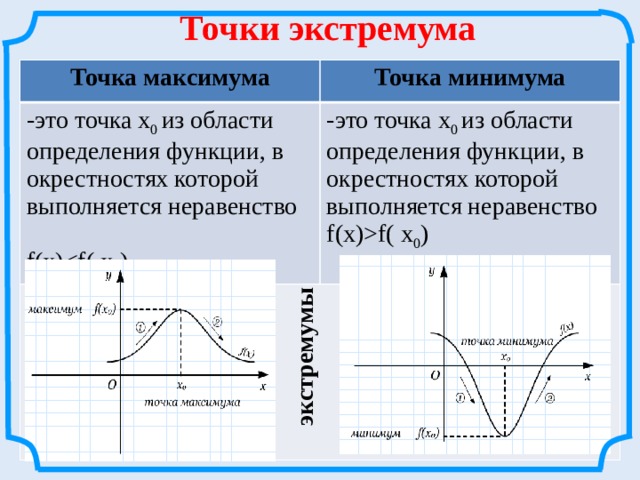
Точки экстремума
экстремумы
Точка максимума
-это точка х 0 из области определения функции, в окрестностях которой выполняется неравенство
Точка минимума
f(x)
-это точка х 0 из области определения функции, в окрестностях которой выполняется неравенство f(x)f( х 0 )
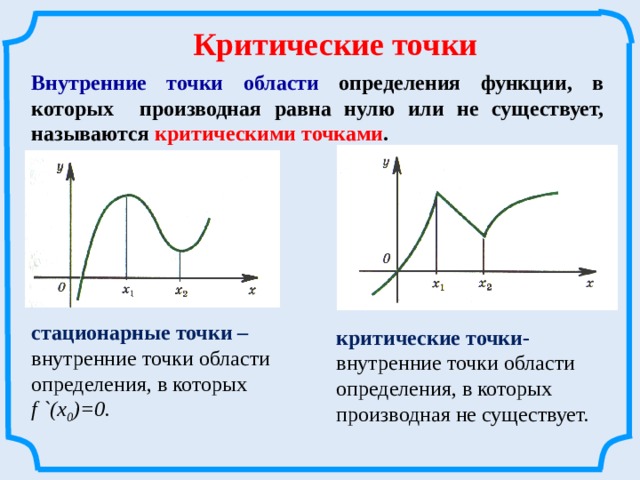
Критические точки
Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками .
стационарные точки –
внутренние точки области
определения, в которых f `(х 0 )=0.
критические точки- внутренние точки области
определения, в которых производная не существует.
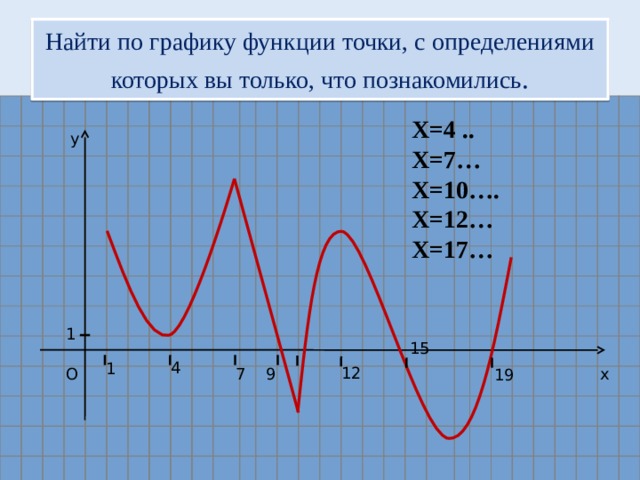
Найти по графику функции точки, с определениями которых вы только, что познакомились .
Х=4 ..
Х=7…
Х=10….
Х=12…
Х=17…
y
1
15
4
1
12
9
7
x
O
19
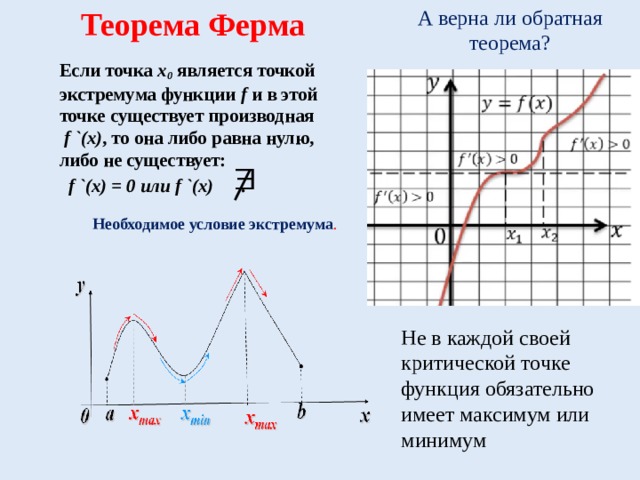
Теорема Ферма
А верна ли обратная теорема?
Если точка х 0 является точкой экстремума функции f и в этой точке существует производная f `(x) , то она либо равна нулю, либо не существует:
f `(x) = 0 или f `(x) .
Необходимое условие экстремума .
Не в каждой своей критической точке функция обязательно имеет максимум или минимум
0 на интервале (а; х 0 ), и f `(x) на интервале (х 0 ; b), то точка х 0 является точкой максимума функции f. Признак минимума функции. Если функция у= f((х) непрерывна в точке х 0 , f `(x) на интервале (а; х 0 ) и f `(x) 0 на интервале (х 0 ; b) , то точка х 0 является точкой минимума функции f " width="640"
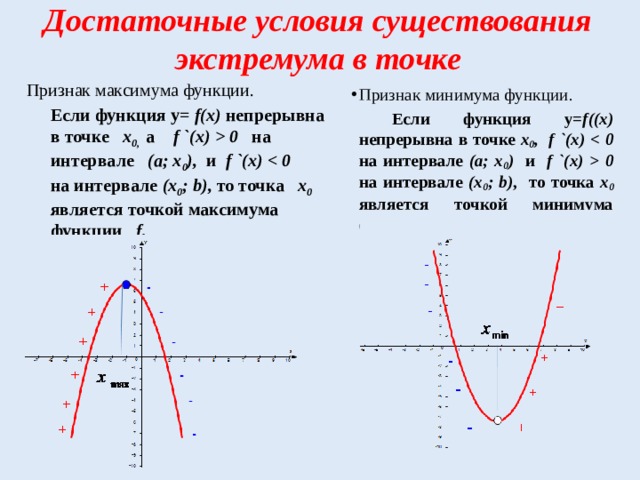
Достаточные условия существования экстремума в точке
Признак максимума функции.
Если функция у= f(х) непрерывна в точке х 0 , а f `(x) 0 на интервале (а; х 0 ), и f `(x) на интервале (х 0 ; b), то точка х 0 является точкой максимума функции f.
- Признак минимума функции.
Если функция у= f((х) непрерывна в точке х 0 , f `(x) на интервале (а; х 0 ) и f `(x) 0 на интервале (х 0 ; b) , то точка х 0 является точкой минимума функции f
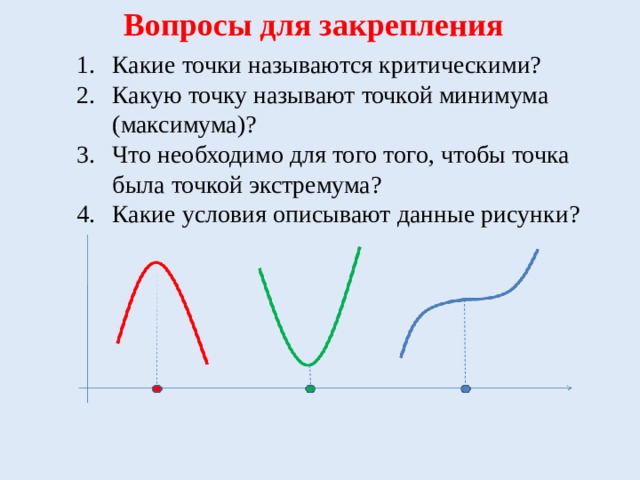
Вопросы для закрепления
- Какие точки называются критическими?
- Какую точку называют точкой минимума (максимума)?
- Что необходимо для того того, чтобы точка была точкой экстремума?
- Какие условия описывают данные рисунки?
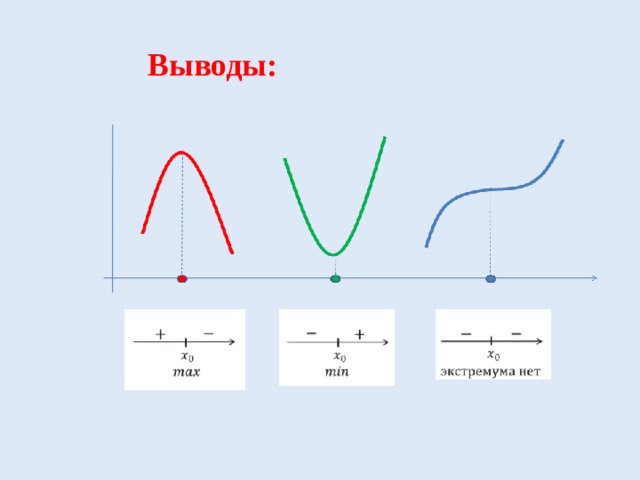
Выводы:
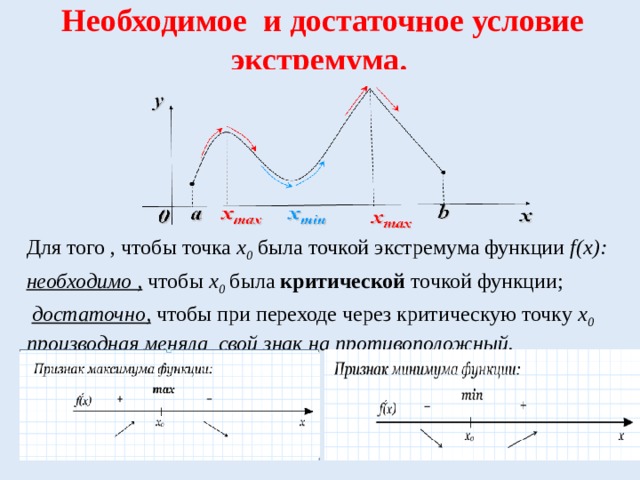
Необходимое и достаточное условие экстремума.
Для того , чтобы точка х 0 была точкой экстремума функции f(х):
необходимо , чтобы х 0 была критической точкой функции;
достаточно, чтобы при переходе через критическую точку х 0 производная меняла свой знак на противоположный.
Найдите точку минимума функции
Найдите точку максимума функции
Задания для самостоятельного решения
1А. (5б) Найдите критические точки функции. Выясните, какие из этих точек являются:
а) точками минимума; б) точками максимума.
№ п/п
1.
дескрипторы
балл
Находит правильно производную
2.
1
3.
Находит критические точки
4.
1
Расставляет верно знаки производной
5.
Определяет точки минимума
1
1
Определяет точки максимума
1
минимума
Задания для самостоятельного решения
2Б. (6б) Найдите экстремумы функции:
№ п/п
дескрипторы
1.
балл
Находит область определения
2.
Находит правильно производную
3.
1
1
Находит критические точки
4.
Расставляет верно знаки производной
5.
1
1
Определяет точки экстремума
6.
Находит экстремумы функции
1
1
Задания для самостоятельного решения
3С.(7б)Найдите промежутки возрастания и убывания, точки экстремума функции:
№ п/п
дескрипторы
1.
балл
Находит область определения
2.
Находит производную
1
3.
1
Находит критические точки
4.
Расставляет знаки производной
1
5.
Исследует поведение функции
6.
1
Находит промежутки монотонности
1
7.
1
Определяет точки экстремума
1
Дополнительные цифровые ресурсы
Ссылки на дополнительные ресурсы для самообразования
https:// bilimland.kz /ru/subject/algebra/10-klass/kriticheskie-tochki-dostatochnoe-uslovie-sushestvovaniya-ehkstremuma?mid=%info%
https:// www.yaklass.ru/ p/algebra/10-klass/proizvodnaia-9147/primenenie-proizvodnoi-dlia-issledovaniia-funktcii-na-monotonnost-i-ekstr_-11226
Продолжи фразу:
Рефлексия содержания учебного материала
Теперь я могу…
Было трудно…
Сегодня я узнал…
Дорогие дети! Вы получили самое основное содержание по новой теме, другие материалы вы получите от своего учителя! Если у вас есть вопросы, вы их можете задать учителю! Удачи в освоении нового материала, наши юные друзья!
Критические точки, точки экстремумафункции (3.46 MB)
0
3354
459
Нравится
0
