Конспект урока " Решение задач с помощью уравнений"

Решение задач с помощью уравнений

Цели:

Образовательная цель: совершенствовать умение решать уравнения с помощью свойств уравнений; отрабатывать умение решать задачи алгебраическим способом;

Воспитательная цель: воспитывать ответственное отношение к учебному труду;

Развивающая цель: развивать устную и письменную математическую речь; прививать интерес к математике.

Тип урока: формирование умений и навыков

Ход урока

І. Организационный момент

ІІ. Проверка домашнего задания

ІІІ. Актуализация опорных знаний

Диктант:

1. Корни уравнения изменяются, если обе части уравнения умножить на число (-10) (Нет)

2. Может ли разность двух отрицательных чисел быть целым положительным числом? (Да)

3. Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак (Да)

4. Если перед скобками стоит знак «–», то нужно раскрыть скобки, сохранив знаки слагаемых (Нет)

5. На ноль делить можно (Нет)

6. Чтобы сложить подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть (Да)

7. Если перед скобками стоит знак «+», то можно опустить скобки, сохранив знаки слагаемых (Да)

8. Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел (Нет)

9. Произведение может быть равно нулю, когда хотя бы один из множителей равен нулю (Да)

10. Может ли сумма двух целых положительных чисел быть равной 0?(Нет)

Учащиеся обмениваются тетрадями. Проверка: – v v – – v v – v –

Оценивание работы на полях: “5” – 10-9 верных знаков, “4” – 7-8 знаков, “3” – 6-5 знака.

IV. Формирование умений и навыков

№ 641 (б)

Задача Пифагора

Говорят, что на вопрос о том, сколько у него учеников, древнегреческий математик Пифагор отвечает так: «половина моих учеников изучает математику, четверть изучает природу, седьмая часть проводит в молчаливом размышлении, остальную часть составляют три девы». Сколько учеников в классе у Пифагора?

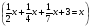х = 28 Ответ:28 учеников.

V. Итог урока

VI. Домашнее задание п 3.10, № 640, 641(а)