Конспект урока по геометрии 9 класс
«Уравнение прямой»
Подготовила: учитель математики
МОУ СОШ №1 г.о. Орехово-Зуево
Романычева Н.В.
Цель: вывести уравнение прямой и показать его применение на практике
Задачи:
- развить умения и навыки при составлении уравнении прямой
- развитие познавательного интереса к предмету
- развить образное и логическое мышление
- воспитать настойчивость в достижении цели
Ход урока
1. Проверка д/з. Выполнение небольшой проверочной работы, направленной на выявление уровня знаний по изученной теме «Уравнение окружности»
| Вариант 1 | Вариант 2 |
| 1. Написать координаты центра окружности и радиус по данному уравнению | |
| а) (х + 8)2 + (у - 5)2 = 16 б) х2 + (у - 10)2 = 25 | а) (х - 4)2 + (у + 2)2 = 4 б) (х + 7)2 + у2 = 9 |
| 2. Написать уравнение окружности радиуса r с центром в точке О | |
| а) О (0; 5), r = 3 б) О (- 3; - 7), r = 6 | а) О (- 1; 2), r = 2 б) О (4; - 3), r = 10 |
| 3. Написать уравнение окружности с центром в начале координат, проходящей через точку | |
| А(- 6; 8) | В (- 4; 3) |
2. Китайская пословица гласит: « Я слышу, - я забываю. Я вижу, - я запоминаю. Я делаю, - я усваиваю». Учащимся предлагается выполнить практическое задание.
1) начертить координатную плоскость
2) провести в ней какую-нибудь прямой
3) отметить на ней 2 точки А (х1; у1) и В (х2; у2)
4) записать уравнение прямой в виде (х – х1)2 + (у – у1)2 = (х – х2)2 + (у – у2)2, подставив вместо х1, у1, х2, у2 значения получившихся координат.
5) далее выполняется раскрытие скобок и преобразование выражения.
Например, А(2; -3) и В (- 5; 4). Получим (х - 2)2 + (у + 3)2 = (х + 5)2 + (у - 4)2
х2 – 4х + 4 + у2 + 6у + 9 = х2 + 10х + 25 + у2 – 8у + 16
-14х + 14у – 28 = 0, разделим всё уравнение на – 14
х – у + 2 = 0 – получили уравнение прямой изображенной на рисунке.
В общем виде уравнение прямой записывается в виде ах + by + c = 0.
3. Рассмотрим различные случаи
| a = 0, b
| a | a | a |
4. Выполнение практических заданий
№1. Определить через какую из точек А(- 10; 7), В(5; 0), С( -5; 3) проходит прямая х + 5у – 25 = 0.
Ответ: А
№2. Найти координаты точки пересечения прямых 2х + у – 1 = 0 и 3х – 2у + 2 = 0.
Ответ: (0; 1)
№3. Написать уравнение прямой, проходящей через точки Е (2; 5) и С (- 3; 7)
Ответ:
№4. Найти координаты точек пересечения с осями координат и начертить прямую 3х – 4у + 12 = 0.
Ответ:
5. Подведение итогов урока
- Уравнение прямой в прямоугольной системе координат является уравнением первой степени.
- Уравнение ах+by+c=0 является уравнением прямой в заданной прямоугольной системе координат.
- Уравнение прямой параллельной одной из координатных осей имеет вид у=у0 или х=х0.При этом ось Ох имеет уравнение у=0, а ось Оу имеет уравнение х=0.
- Координатами точки пересечения прямых является решение системы уравнений, задающих эти прямые.
Домашнее задание: № 972, №978.

 Получите свидетельство
Получите свидетельство Вход
Вход



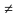 0, y = m
0, y = m








 Конспект урока по геометрии в 9 классе по теме "Уравнение прямой" (16.84 KB)
Конспект урока по геометрии в 9 классе по теме "Уравнение прямой" (16.84 KB)
 0
0 947
947 144
144 Нравится
0
Нравится
0


