04.09.2019г. 6 кл.
Урок № 1: Дроби. Основное свойство дроби
Цели урока:
1. Образовательные: ввести основное свойство дроби; сформировать умение применять данное свойство на практике; ввести новое действие сокращение дробей.
2. Воспитательные: воспитание аккуратности, дисциплины, настойчивости, ответственного отношения к учебе.
3. Развивающие: развитие памяти, речи, любознательности, познавательного интереса;
формирование представлений о математическом языке, развитие коммуникативных умений и навыков.
Ход урока
1. Постановка цели урока.
Добрый день, ребята! Как ваше настроение? Давайте поприветствуем друг друга улыбкой и сохраним хорошее настроение в течение всего урока.
Ребята, нужны ли в жизни человеку математические знания?
А математика может обойтись без дробей?
Почему? Что обозначает слово «дробь»?
В русском языке слово «дробь» появилось в 8 веке, оно происходит
от глагола «дробить» - разбивать, ломать на части. В первых учебниках математики (в 17 веке) дроби так и назывались – «ломанные числа».
Современную систему записи дробей с числителем и знаменателем создали в Индии. Только там писали знаменатель сверху, а числитель снизу и не писали дробной черты. На
Руси дроби называли долями, позднее «ломаными числами». Перед вами названия некоторых дробей:
1/2 - половина, полтина;
1/3- треть;
1/6 – полтреть;
1/4 - четь; 1/8 – полчеть:
1/5 – пятина;
1/10 – десятина.
Дробная черта появилась в записи дробей лишь около 300 лет назад. Названия "числитель и знаменатель" ввел в употребление греческий математик Максим Плануд. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка "попасть в дроби", что означает попасть в трудное положение.
- Хорошо. И так мы знаем, что дроби можно получить двумя способами. Знаем, что обыкновенная дробь обозначает. (Что-то целое разделили на н частей и взяли таких частей м.)
- Чем же мы сегодня на уроке будем заниматься? Как вы думаете?
2. Устный счёт
С помощью моделей обыкновенных дробей покажите дроби и объясните, что обозначает числитель и знаменатель каждой дроби.
5/12
3/8
5/6
3. Объяснение нового материала.
А сейчас используя модели дробей проиллюстрируйте дроби:
6/8
9/12
3/4
- Что вы можете заметит, какие дроби получились по величине? (Равные.)
- Можно ли между этими дробями поставить знак равенства? (Да.)
6/8 = 9/12 = 3/4
- Как из дроби 3/4 можно получить дробь 6/8? (3 * 2/4 * 2)
- Как из дроби 3/4 можно получить дробь 9/12? (3 * 3/4 * 3)
Т.е. для получения равных дробей можно числитель и знаменатель делить на одно и тоже число.
Вывод: при умножении и делении числителя и знаменателя дроби на одно и тоже число (кроме нуля) ее величина не изменится.
Это свойство очень важное и его называют основным свойством дроби.
Тема нашего урока так и называется «Дроби. Основное свойство дробей».
Открываем тетради, записываем дату, классная работа и тему урока. Открыли учебник на стр. 8 и прочитали данное свойство. Отметили важные слова в этой формулировке. (Числитель, знаменатель и равные.)
4. Закрепление нового материала.
№3
№4 (а)
№6 (а,г)
З: №1(а,б)
№2(а,б)
5. Организация и самоорганизация урока

6. Практикум
З:
№3 (а,б,в)
№4-7 (а)

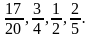
У: №11
8. Домашнее задание
У: стр. 8-9 – читать; № 1, 2, 4(б), 5, 8.
Продвинутым: № 6(в, д).

 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект к уроку по теме "Дроби. Основное свойство дроби" (63.22 KB)
Конспект к уроку по теме "Дроби. Основное свойство дроби" (63.22 KB)
 0
0 302
302 16
16 Нравится
0
Нравится
0



