Захарова Г.С. учитель математики
Повторение темы
“Решение текстовых задач в IX классе”
“Деятельность учителя в ходе изучения темы
неотделима от деятельности учащихся...
Она должна состоять из трех основных этапов:
мотивационного, операционно-познавательного
и рефлексивно-оценочного.”
Фридман Л.М
Рассмотрим эту деятельность на примере одного из уроков итогового повторения темы “Решение текстовых задач в IX классе”.
На первом, мотивационном, этапе мы вместе с учащимся обсудили почему и для чего необходимо повторить эту тему, оцениваем свои возможности и составляем план работы.
Повторить тему за 8 уроков;
Задачи на движение;
.Задачи на совместную работу;
. Задачи на планирование;
.Задачи на проценты;
.Задачи с геометрическим содержанием;
.Задачи на смеси (сплавы).
Задачи, которые предлагаются учащимся в школьном учебнике, усваиваются достаточно хорошо. Поэтому при повторении я решила использовать различные пособия по элементарной математике и сборник для подготовки к итоговой аттестации.
Моя цель: в процессе повторения учащиеся должны последовательно перейти от одного уровня математической деятельности к следующему, более высокому, сделав для себя открытие.
Мотивация учащихся: готовятся к выпускным экзаменам, расширяют и углубляют знания по данной теме.
Рассмотрим один из уроков решения задач на движение.
Я попросила учащихся подобрать задачи на движение и в одном направлении.
Необходимо было выбрать задачи из первой части и задачи из второй части, которые выходят за рамки традиционных. Учащиеся выполнили творческую работу, при выполнении которой они открыли для себя что-то новое. Пройден этап математической деятельности: накопление фактов с помощью наблюдений, опыта, обощения. Учащиеся использовали как арифметические способы рассуждений , так и алгебраический метод (составление выражений, уравнений, систем).
На данном уроке мы решили рассмотреть следующие задачи:
Из города А в город В, расстояние между которыми 120 км, выехали одновременно два велосипедиста. Скорость первого на 3 км/ч больше скорости второго, поэтому он прибыл в город В на 2 часа раньше. Определите скорости велосипедистов.
Из пунктов А и В расстояние между которыми 19 км, вышли одновременно навстречу друг другу два пешехода и встретились в 9 км от пункта А. Найти скорость каждого, если известно, что пешеход, вышедший из А, шел со скоростью, на 1 км/ч большей, чем второй пешеход, и сделал в пути получасовую остановку.
Велосипедист от озера до деревни ехал со скоростью 15 км/ч, а обратно- со скоростью 10 км/ч. Сколько времени ушло у него на дорогу от озера до деревни, если на весь путь туда и обратон велосипедист затратил 1 час? Пусть х часов- время, затраченное на дорогу от озера до деревни. Какое уравнение соответствует условию задачи?
А. 15х=10(1-х) . В. 15х+10(1-х)=1.
Б. 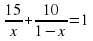 Г. 15(1-х)= 10 х.
Г. 15(1-х)= 10 х.
От города до поселка автомобиль доехал за 3 часа. Если бы он увеличил скорость на 25 км/ч , то затратил бы на этот путь на 1 час меньше.
Чему равно расстояние от города до посёлка?
Пусть х км – расстояние от города до посёлка. Какое уравнение соответствует условию задачи?
А. 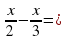 25 В.
25 В. 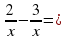 25
25
Б. 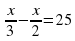 Г.
Г. 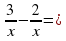 25
25
Пешеход вышел из пункта А в пункт В. Через 45 минут из А в В выехал велосипедист. Когда велосипедист прибыл в В, пешеходу оставалось пройти 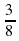 всего пути.
всего пути.
Сколько времени потратил пешеход на весь путь, если известно, что велосипедист догнал пешехода на половине пути из пункта А в В, а скорости пешехода и велосипедиста постоянны?
Два пешехода вышли одновременно из своих сел А и В навстречу друг другу. После встречи первый шел 25 минут до села В, а второй шел 36 минут до села А.
Сколько минут они шли навстречу друг другу?
Второй этап деятельности- операционно-познавательный.
Над этими задачами учащиеся работали дома и выполнили задания: классификация задач по виду; по методам решения; по виду ответа; решение уравнения.
Урок начинаю с вопроса:
Как классифицировали задачи по виду?
Ответ: Мы рассмотрели задачи на движение навстречу друг другу и в одном направлении.
Какими методами можно решить эти задачи?
Ответ: Составлением уроавнения или системы уравнений; арифметический способ.
К сожалению, никто не назвал геометрический способ решения задачи
Что можете сказать о видах ответа?
Ответ: решение уравнений или систем уравнений; с выбором ответа.
На последнем, рефлексивно-оценочном, этапе учащиеся анализировали свою собственную деятельность, оценивали её, сопоставляя результаты своей деятельности с результатами товарищей.
Задачи № 1 и №2 затруднений не вызвали. Перед решением на доске учащиеся прокомментировали : задачи можно решить составлением уравнения или системы уравнений.
№1.
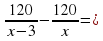 2 и
2 и 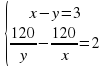
№2.
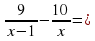
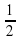 или
или 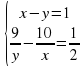
Решение уравнений и систем уравнений затруднений не вызвало, так как тема была уже повторена.
Задачи № 3 и №4- с выбором ответа. Задачи были решены у всех без исключения с последеющим объяснением выбора, четко и грамотно.
Задачи № 5. Данная задача у всех была решена одинаково. Учащиеся составили и решили уравнение
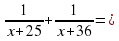
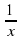
Это уравнение имеет единственный положительный корень х=30. Следовательно, пешеходы шли до встречи 30 минут.
Вопрос: можно ли решить задачу вторым способом?
Вопрос вызвал затруднение, и тогда я оказала помощь в построении графиков движения. Далее учащиеся сами увидели пару подобных треугольников, составили пропорцию и решили её. Решение вызвало живой интерес.
II Способ. Пусть до встречи пешеходы шли х мин. Посторим график движения пешеходов.
Из подобия двух пар треугольников (по двум углам) следует, что
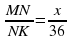 и
и 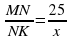 . Составим уравнение
. Составим уравнение 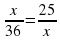 .
.
Это уравнение имеет единственный положительный корень x=30. Следовательно, пешеходы шли до встречи 30 минут.
Ответ: 30 мин.
Задачу № 5 решили арифметическим способом, выполнив одно единственное действие:
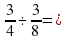
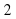 (ч)
(ч)
Алгебраический способ вызвал затруднение, поэтому решили задачу вместе.
Решение: Пусть время движения пешехода из А и В составляет x ч., а время движения велосипеда из А и В составляет у ч. Тогда на половину пути пешеход завтратил 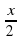 ч, что равно
ч, что равно 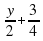 . Составим первое уравнение:
. Составим первое уравнение: 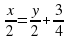
Так как при движении с постоянной скоростью пройденное расстояние пропорционально времени движения, то в тот момент, когда велосипедист прибыл в В, пешеход прошёл 1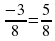 расстояния от А до В и затратил на это
расстояния от А до В и затратил на это 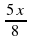 ч., что равно
ч., что равно 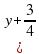 ) ч. Составим второе уравнение:
) ч. Составим второе уравнение: 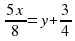 .
.
Решив систему уравнений :
Найдём , что x=2, у=5. То есть время движения пешехода их А в В составляет 2 часа.
В конце подведем итоги: учащиеся испытали радость победы над трудностями, познали новые приемы решения алгебраических задач, дали самооценку своей деятельности. Оцениваем работу учащихся на уроке.
Задание на дом: сборник 8.3;
8.10;
8.31;
8.33.
Литература
1. Сборник заданий для подготовки к государственной итоговой аттестации в 9 кл. 2014 г.
2. Шевкин А.В. Курс лекций “Текстовые задачи в школьном курсе математики” (5-9 кл.)
3.Интсруктивно- методическое письмо о преподавании математики в общеобразовательных учреждениях Московской области.
4. Кодификаторы элементов и требований к уровню подготовки выпускников IX кл.


 Получите свидетельство
Получите свидетельство Вход
Вход



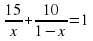 Г. 15(1-х)= 10 х.
Г. 15(1-х)= 10 х.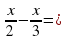 25 В.
25 В. 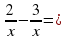 25
25 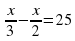 Г.
Г. 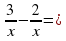 25
25 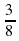 всего пути.
всего пути. 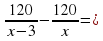 2 и
2 и 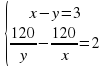
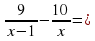
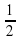 или
или 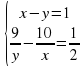
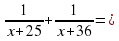
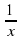
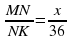 и
и 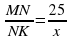 . Составим уравнение
. Составим уравнение 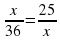 .
.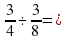
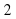 (ч)
(ч)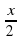 ч, что равно
ч, что равно 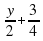 . Составим первое уравнение:
. Составим первое уравнение: 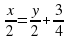
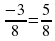 расстояния от А до В и затратил на это
расстояния от А до В и затратил на это 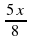 ч., что равно
ч., что равно 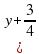 ) ч. Составим второе уравнение:
) ч. Составим второе уравнение: 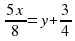 .
. 








 Конспект урока по математике по теме "Решение текстовых задач в IX классе" (26.43 КB)
Конспект урока по математике по теме "Решение текстовых задач в IX классе" (26.43 КB)
 0
0 2539
2539 398
398 Нравится
0
Нравится
0


