Министерство образования Республики Башкортостан
ГБОУ СПО «Уфимский государственный колледж технологии и
дизайна»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА ОТКРЫТОГО УРОКА
«Правила дифференцирования»

Ишбулатова АйсылуШамилевна,
преподаватель математики
Уфа 2014
Пояснительная записка
Методическая разработка занятия разработана преподавателем математики А.Ш. Ишбулатовой.
Тема методической разработки – «Правила дифференцирования». Методическая разработка состоит из технологической карты занятия, плана-конспекта занятия и приложения. В технологической карте занятия определяются цели занятия – обучающие, развивающие, воспитывающие. Указаны оборудование и наглядные пособия, литература. План-конспект урока представляет собой подробное изложение всего хода занятия. В приложении содержится раздаточный материал.
Изучение производной – достаточно сложный процесс, однако усвоение этого материала является очень важным. Ведь понятие производной является фундаментальным для более сложных разделов математики. Человек в повседневной деятельности постоянно сталкивается с решением задач, которые могут быть полностью описаны с помощью функций на математическом языке, а между тем производная является мощным орудием исследования функций. Процесс нахождения производной называется дифференцированием. Чаще всего, функция может быть представлены в виде суммы, разности, произведения, частного элементарных функций, поэтому изучения производной невозможно без знаний правил дифференцирования.
Изучение любой темы должно сопровождаться решением большого количества упражнений, что позволяет выработать у учащихся необходимые практические навыки. Поэтому в данной работе разработана система упражнений, для наиболее полного усвоения учебного материала.Приобретение студентами знаний и умений по расчету производных способствует формированию общеучебной компетенции студентов, развитию умений самоорганизации учебной деятельности при выполнении заданий.
Данный урок представляет собой урок изучения нового материала. Он включает в себя этап актуализации опорных знаний, усвоения нового материала и первичного закрепления знаний, а также рефлексии. Самостоятельная деятельность учащихся обеспечивает прочное усвоение новых понятий.
Занятие строится в форме комбинированного урока с элементами лекции, беседы, практической работы, проведения опроса, как для актуализации, так и для закрепления знаний. Используются инновационные образовательные технологии и средства обучения – мультимедийное оборудование, презентация, которые сопровождают объяснение преподавателя.
Занятие проводится с аудиторией, владеющей с понятием производная, производная элементарных функций.
Методическая разработка данного занятия и разработанные преподавателем материалы – презентация, технологическая карта могут быть использованы для проведения занятий по дисциплине «Математика» у студентов I курса всех специальностей в учреждениях среднего и начального профессионального образования.
Технологическая карта занятия
вид урока: комбинированный урок.
Тип урока: изучение нового материала
Дата: 10.12.14
Преподаватель: Ишбулатова А.Ш.
Курс: первый
Группа: ДН-14-29
Дисциплина: Математика
Тема ЗАНЯТИЯ: «Правила дифференцирования»
Цели занятия:
Обучающие:
повторить определение производной, её физический и геометрический смысл;
рассмотреть и изучить основные правила дифференцирования;
отработать навыки нахождения производных суммы, разности, произведения и частного функций
Развивающие:
развить умение анализировать и обобщать полученные знания;
развивать у учащихся практические навыки;
развитие познавательного интереса, памяти и культуры математической речи
Воспитывающие:
формировать чувство ответственности, самостоятельности, аккуратности, оперативности;
формировать познавательные потребности, дисциплинированность, умение работать в коллективе.
Задачи занятия:
Содействовать формированию у учащихся образного мышления;
Развить навыки анализа и самоанализа;
Развить способности к абстрактному мышлению;
ФОРМЫ ОРГАНИЗАЦИИ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ: фронтальная (коллективная), групповая, индивидуальная.
Оборудование:
Литература:
Мордкович. А.Г. Алгебра и начала математического анализа. 10-11кл. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А. Г. Мордкович. – 14-е изд., стер. М.: «Мнемозина», 2013. – 400с.
Мордкович А.Г..Алгебра и начала математического анализа. 10-11кл. В 2 ч. Ч.2. Задачник для учащихся общеобразовательных учреждений (базовый уровень) / [А. Г Мордкович и др.]; под ред. А. Г. Мордкович. – 14-е изд., стер. – М .: «Мнемозина», 2013. – 271с.
план занятия
Организационный этап
приветствие;
проверка отсутствующих.
Актуализация знаний
Постановка темы, цели урока.
Объяснение нового материала.
Закрепление материала. Решение задач.
Практическая работа. Работа с карточками.
Историческая справка. Выступление учащийся с докладом о Г. Лейбнице.
Домашняя работа
Рефлексивно-оценочная часть урока.
Подведение итогов урока
содержание занятия
Организационный момент.
Здравствуйте! Прошу садиться.
Преподаватель заполняет журнал и проводит проверку отсутствующих.
Актуализация знаний.
Сегодня на уроке вы сами себя будете оценивать. У каждого из вас на столе лежит лист самоконтроля, после каждого выполненного задания не забывайте его заполнять (Приложение А).
Кроссворд по теме «Производная» (слайд 1)
|
|
|
|
|
|
|
|
| 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
|
|
| 6 |
| 8 |
| 10 |
|
|
| 2 | 3 |
|
|
| 7 |
|
|
| 11 |
|
|
|
| 4 |
|
|
|
|
|
|
|
| 1 п | р | о | и | з | в | о | д | н | а | я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знак обозначения действия сложения (плюс).
Сумма длин всех сторон многоугольника (периметр).
Геометрическая фигура, состоящая из двух лучей (луч).
Тригонометрическая функция (синус).
Часть прямой, заключенная между двумя точками (отрезок).
Равенство, содержащее переменную (уравнение).
Сотая часть числа (процент).
Единица измерения угла (градус).
Сторона прямоугольного треугольника, лежащая против прямого угла (гипотенуза).
Часть окружности, заключенная между двумя точками (дуга).
График линейной функции (прямая).
Фронтальный опрос
Что называется приращением аргумента.
Что называется приращением функции.
3. В чем состоит геометрический смысл производной функции.
4. В чем состоит механический смысл производной функции.
5. Дайте определение производной функции f(x) в точке х0
А теперь давайте повторим таблицу производных: (слайды 2-15)
Проверим знания с помощью теста, который содержит 13 вопросов (учащимся раздается тест (Приложение С), который они делают самостоятельно, а затем все вместе проверяем). Если ответ правильный, то ставят 1 балл)
Постановка цели, темы урока.
Какие пункты теста вызвали у вас наибольшее затруднение? (предполагаемый ответ учащихся – 10, 11, 12, 13).
Давайте попробуем выяснить, где именно возникло затруднение и почему? (при нахождении производной суммы, разности, произведения и частного двух функций).
Что нужно сделать, чтобы преодолеть это затруднение? (сформулировать правило нахождения производной).
А как называется процесс нахождения производной? (дифференцированием)
Какая же будет цель нашей деятельности на уроке сегодня? (Изучение основных правил дифференцирования).
Цель урока: Изучение основных правил дифференцирования в нахождении производной суммы, разности, произведения и частного функций.А теперь попробуйте сформулировать тему урока (Правила дифференцирования).
Запишите число и тему урока в тетрадях «Правила дифференцирования» (слайд 16).
Объяснение нового материала
Сформулируем и запишем основные правила дифференцирования.
Правило 1. Если функции 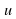 и
и 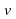 дифференцируемы в точке х0, то их сумма (разность) дифференцируема в этой точке и
дифференцируемы в точке х0, то их сумма (разность) дифференцируема в этой точке и 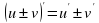
Коротко говорят: производная суммы равна сумме производных (слайд 17).
Правило 2. Если функция 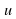 дифференцируема в точке х0, то функция
дифференцируема в точке х0, то функция 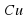 дифференцируема в этой точке и
дифференцируема в этой точке и 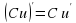 .
.
Коротко говорят: постоянный множитель можно выносить за знак производной (слайд 18).
Правило 3. Если функции u и 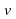 дифференцируемы в точке х0, то их произведение дифференцируемо в этой точке и
дифференцируемы в точке х0, то их произведение дифференцируемо в этой точке и 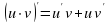 (слайд 19).
(слайд 19).
Правило 4. Если функции u и 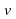 дифференцируемы в точке х0 и функция v не равна нулю в этой точке, то частное дифференцируемо в этой точке и
дифференцируемы в точке х0 и функция v не равна нулю в этой точке, то частное дифференцируемо в этой точке и 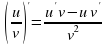 (слайд 20).
(слайд 20).
Вернемся к примерам теста и решим их (учитель решает примеры у доски, используя основные формулы).
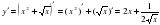 ;
;
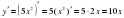 ;
;
-
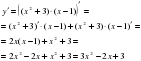 ;
;
4.
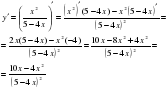
Закрепление материала. Решение задач.
Учащиеся выполняют упражнения из учебника с объяснением у доски:
№ 28.15(а,б), 28.16 (а,б), 28.18(а, б), 28.21
Отвечают у доски на оценку и записывают решения этих примеров в тетрадь.
Практическая работа.
Каждому учащемуся выдается набор карточек. Каждый учащийся выполняет самостоятельно задания на карточках, причем решение записывает в тетрадь.
На карточке написано задание, они должны его выполнить и ответ написать с обратной стороны в квадратик. Когда выполните все задания, расположите карточки в порядке возрастания полученных ответов, и вы получите слово. У одних учащихся получится имя, а у других фамилия ученого, с которым тесно связано понятие производной – Готфрид Лейбниц (Приложение D).
Историческая справка. Выступление учащейся с докладом о Г. Лейбнице (слайд 24).
Домашнее задание.
Выполнить упражнения №.28.15 (в, г), 28.16 (в, г), 28.17(слайд 25).
Рефлексивно-оценочная часть урока. Продолжи фразу (слайд 26):
«Сегодня на уроке я узнал…»
«Сегодня на уроке я научился…»
«Сегодня на уроке я повторил…»
«Сегодня на уроке я закрепил…»
«Сегодня на уроке мне понравилось…»
Учащиеся сдают лист самоконтроля, каждый получает оценку.
Приложение А
ЛИСТ САМОКОНТРОЛЯ
Фамилия, имя __________________________________________________
Критерии оценки всех заданий.
Кроссворд по теме «Производная». За каждое отгаданное слово 1 балл. Максимальное количество баллов – 11 .
Фронтальный опрос. За каждый вопрос 1балл, максимальное количество баллов – 5, (если не отвечал, ставим прочерк за это задание).
Тест, за каждый пункт 1балл, максимальное количество баллов – 13.
Работа у доски: 1 балл.
Практическая работа. За каждую карточку 1 балл. Максимальное количество баллов – 7.
Критерии оценки за урок:
«3» - 19-15 баллов
«4» - 26-30 баллов
«5» - 31-37 баллов
| Вид задания | 1 | 2 | 3 | 4 | 5 | | Итого баллов | Оценка |
| Количество баллов
|
|
|
|
|
|
|
|
Приложение В
Кроссворд по теме «Производная»
|
|
|
|
|
|
|
|
| 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
|
|
| 6 |
| 8 |
| 10 |
|
|
| 2 | 3 |
|
|
| 7 |
|
|
| 11 |
|
|
|
| 4 |
|
|
|
|
|
|
|
| 1 п | р | о | и | з | в | о | д | н | а | я |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знак обозначения действия сложения
Сумма длин всех сторон многоугольника
Геометрическая фигура, состоящая из двух лучей
Тригонометрическая функция
Часть прямой, заключенная между двумя точками
Равенство, содержащее переменную
Сотая часть числа
Единица измерения угла
Сторона прямоугольного треугольника, лежащая против прямого угла
Часть окружности, заключенная между двумя точками
График линейной функции.
Приложение С
Тест «Таблица производных
Производная функции 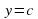 равна
равна
| 1. 0; | 2. 1; | 3. 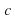 . . |
Производная функции 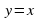 равна
равна
| 1. 0; | 2. 1; | 3. 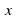 . . |
Производная функции 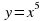 равна
равна
Производная функции  равна
равна
Производная функции  равна
равна
Производная функции  равна
равна
Производная функции 
 равна
равна
Производная функции 
 равна
равна
Производная функции 
 равна
равна
| 1. 32; | 2.  ; ; | 3. 0 |
Производная функции 
 равна
равна
Производная функции 
 равна
равна
Производная функции  равна
равна
Производная функции 
 равна
равна
Приложение D
|
Вычислите значение производной функции y = x2 2x+3 в точке x0 = 3.
|
Вычислите значение производной функции y = 3x + 2 в точке в точке x0 = 4.
|
Вычислите значение производной функции y = в точке в точке x0 =  . .
|
|
Вычислите значение производной функции y = в точке в точке x0 = 1.
|
Вычислите значение производной функции y =(x + 1)(x2 4)в точке x0 = 0.
|
Вычислите значение производной функции y = в точке x0 = 1. в точке x0 = 1.
|
|
Вычислите значение производной функции y = в точке x0 = 2. в точке x0 = 2.
|
|
|
|
Вычислите значение производной функции y = 2 + 5x + x2 в точке x0 = 3.
|
Вычислите значение производной функции y = 2x + 3 в точке в точке x0 = 1.
|
Вычислите значение производной функции y = в точке в точке x0 = 0.
|
|
Вычислите значение производной функции y =7x +  в точке x0 = 1. в точке x0 = 1.
|
Вычислите значение производной функции y =(3x + x2) ·x2в точке x0 = 0.
|
Вычислите значение производной функции y = в точке x0 = 1. в точке x0 = 1.
|
|
Вычислите значение производной функции y = в точке x0 = 2. в точке x0 = 2.
|
|
|



 Получите свидетельство
Получите свидетельство Вход
Вход




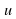 и
и 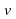 дифференцируемы в точке х0, то их сумма (разность) дифференцируема в этой точке и
дифференцируемы в точке х0, то их сумма (разность) дифференцируема в этой точке и 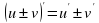
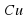 дифференцируема в этой точке и
дифференцируема в этой точке и 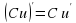 .
.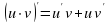 (слайд 19).
(слайд 19).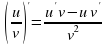 (слайд 20).
(слайд 20).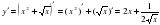 ;
;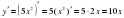 ;
;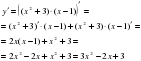 ;
;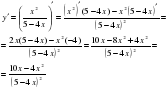
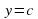 равна
равна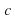 .
.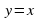 равна
равна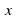 .
.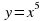 равна
равна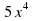 ;
;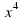 ;
;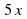 .
.








 Конспект урока по математике по теме "Правила дифференцирования" (0.14 MB)
Конспект урока по математике по теме "Правила дифференцирования" (0.14 MB)
 0
0 2864
2864 465
465 Нравится
0
Нравится
0


