Получите свидетельство
Вход
Комплексные числа
Разработала: Рашидова Ю.Н.,
преподаватель БПОУ ВО «ЧМК»
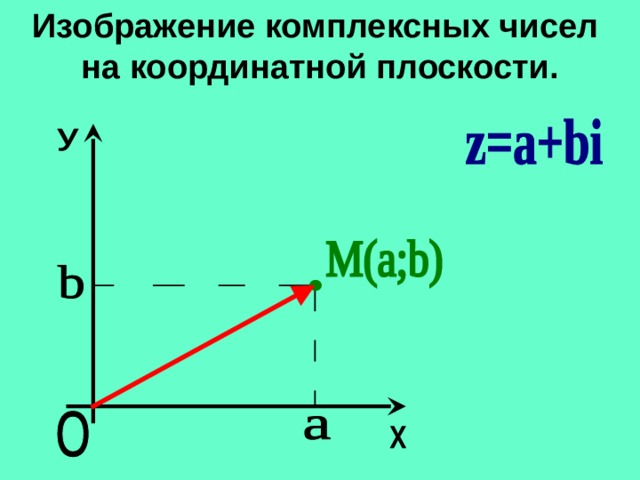
Изображение комплексных чисел на координатной плоскости.
Каждое комплексное число z=a+bi геометрически изображается на плоскости как точка M(a;b) или как вектор ОМ с началом в точке O( 0;0 ) и концом в точке M(a;b) .
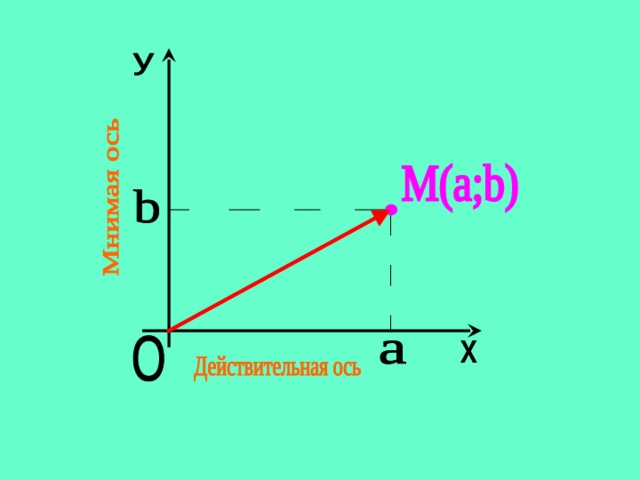
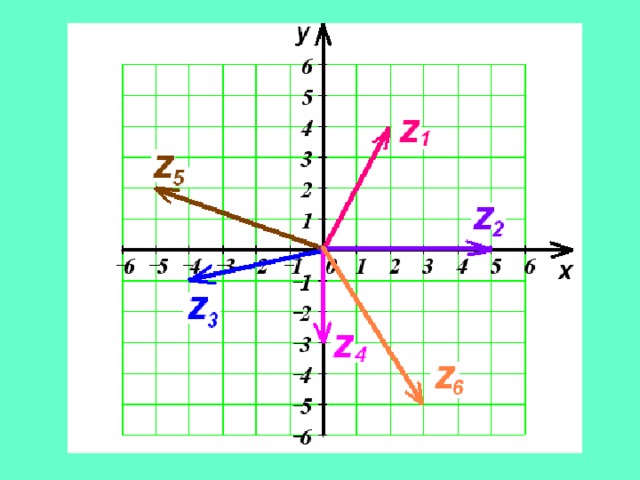
Пример. Изобразить на плоскости комплексные числа:
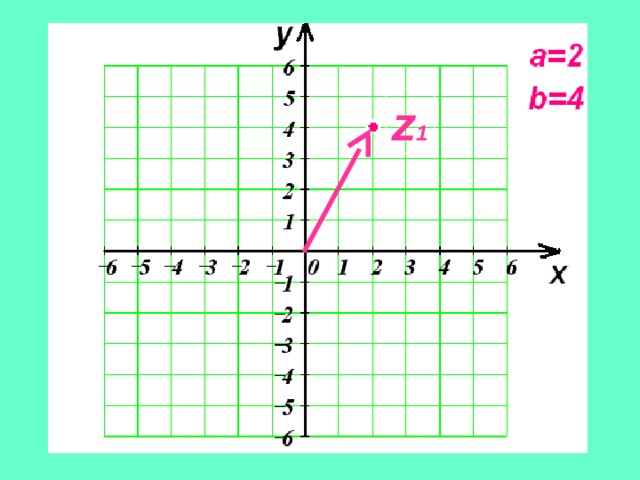
z 1
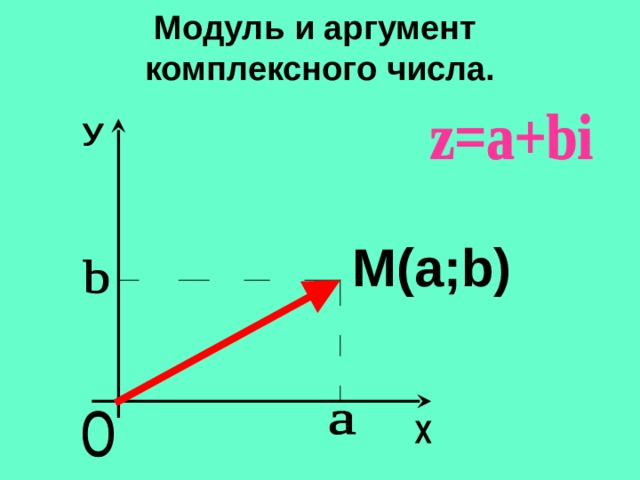
Модуль и аргумент комплексного числа.
M(a;b)
Модулем комплексного числа z=a+bi называется длина вектора, соответствующего этому числу. Обозначение: r , |z|.
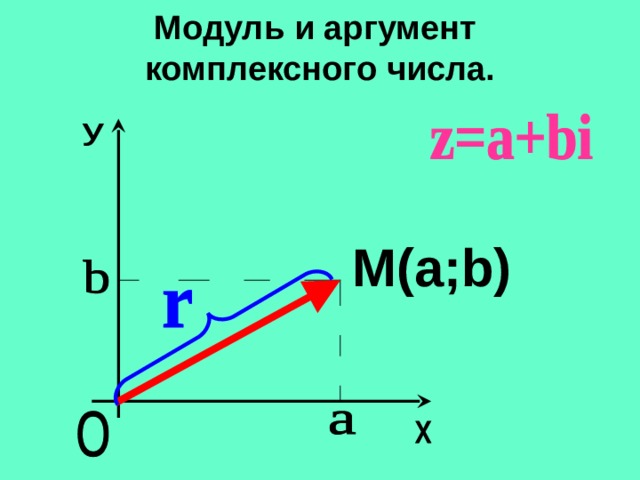
Модуль и аргумент комплексного числа.
M(a;b)
Пример. Найти модуль комплексных чисел:
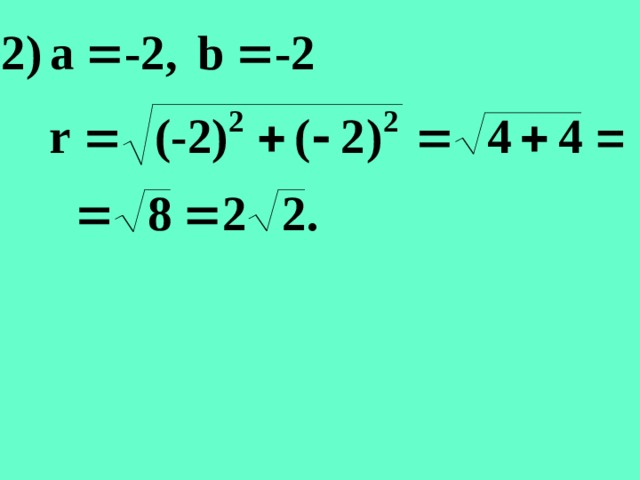
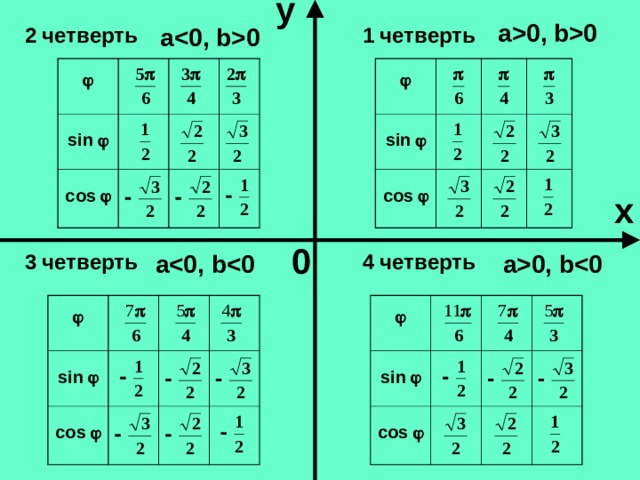
Аргументом комплексного числа z ≠ 0 называется угол , который образует вектор z с положительным направлением оси абсцисс. Обозначение: , argz.
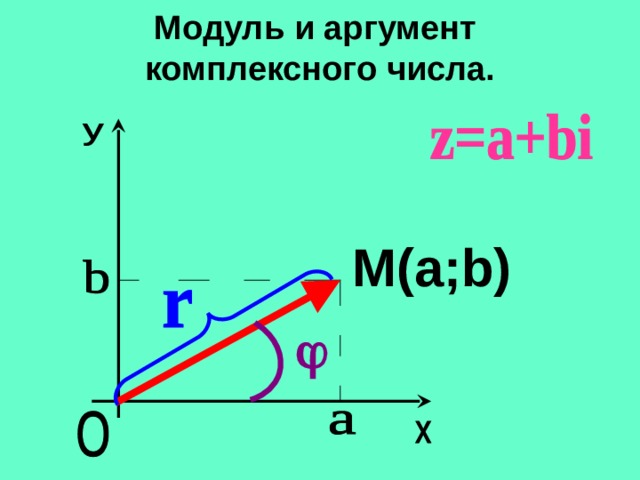
Модуль и аргумент комплексного числа.
M(a;b)
0 , b0 1 четверть 2 четверть a , b0 sin sin cos cos x 0 a0 , b a , b 4 четверть 3 четверть sin sin cos cos " width="640"
y
a0 , b0
1 четверть
2 четверть
a , b0
sin
sin
cos
cos
x
0
a0 , b
a , b
4 четверть
3 четверть
sin
sin
cos
cos
Запись комплексного числа в виде
называется тригонометрической формой комплексного числа.
Запись комплексного числа в виде
называется показательной формой комплексного числа.
Пример.
Алгоритм нахождения тригонометрической и показательной форм к. ч.
Пример.
- Найти a и b и определить, в какой четверти находится данное число.
- Вычислить модуль к. ч., используя фор-лу:
Действия над комплексными числами,
заданными в тригонометрической и
показательной формах.
I. Умножение.
ПРАВИЛО 1.
При умножении двух комплексных чисел, заданных в тригонометрической
или показательной формах, их модули перемножаются, а аргументы складываются.
Пример!
Даны комплексные числа
Найти произведение этих чисел.
Решение.
Пример!
Даны комплексные числа
Найти произведение этих чисел.
Решение.
II. Деление.
ПРАВИЛО 2 .
При делении двух комплексных чисел, заданных в тригонометрической
или показательной формах, их модули делятся, а аргументы вычитаются.
Пример!
Даны комплексные числа
Найти частное этих чисел.
Решение.
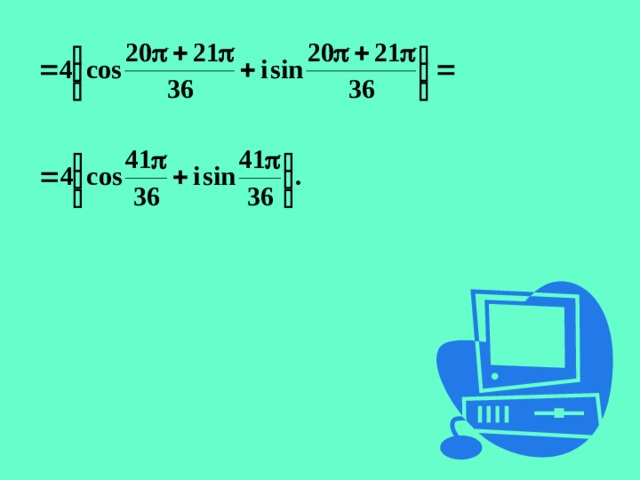
Пример!
Даны комплексные числа
Найти частное этих чисел.
Решение.
II. Возведение в степень.
ПРАВИЛО 3.
При возведении в целую степень комплексного числа, заданного в тригонометрической или показательной формах, модуль числа надо
возвести в эту степень, а аргумент умножить
на показатель степени.
Пример!
Дано комплексное число
Решение.
Пример!
Дано комплексное число
Решение.
Комплексные числа. (839 KB)
0
222
6
Нравится
0
