МОБУ «ООШ №9»
Урок по геометрии, 8 класс
“Касательная к окружности”
Подготовила и провела: Зюзюкина Л.А.
Март 2021
Тема урока: Касательная к окружности, ее свойства.
Урок объяснения нового материала.
Цели урока:
Ввести понятия касательной, точки касания, отрезков касательных, проведённых из одной точки.
Рассмотреть свойство касательной и её признак и показать их применение при решении задач.
Рассмотреть свойство отрезков касательных, проведённых из одной точки и показать его применение в процессе решения задач, направленных на выявление понимания содержания теоремы на уровне узнавания и формально-логическом уровне.
Способствовать формированию приёмов критического мышления, анализа и синтеза.
Воспитание коммуникативной культуры, приобретение опыта самостоятельной работы.
Оборудование: компьютер, презентация, проектор с экраном, доска, тесты.
Орг. момент.
Актуализация опорных знаний.
Мотивация введения данного понятия.
Введение теоремы о касательной к окружности.
Анализ предложенных утверждений (выявление понимания содержания теоремы).
Доказательство теоремы.
Разбор задач.
Подведение итогов и задание ДЗ.
I. Организационный момент.
“Ни 30 лет, ни 30 столетий не оказывают никакого влияния на ясность или на красоту геометрических истин”. Кэрролл Л.
Сообщить тему урока, сформулировать цели урока.
II. Актуализация знаний учащихся
1. Устный опрос. (Цель: вызвать интерес к изучению темы)
1. Верите ли вы, что самая простая из кривых линий – окружность?
2. Верите ли вы, что древние индийцы считали самым важным элементом окружности радиус, хотя не знали такого слова?
3. Верите ли вы, что впервые термин “радиус” встречается лишь в 16 веке?
4. Верите ли вы, что в переводе с латинского радиус означает “луч”?
5. Верите ли вы, что при заданном периметре именно окружность ограничивает наибольшую площадь?
6. Верите ли вы, что в русском языке слово “круглый” означает высшую степень чего-либо?
7. Верите ли вы, что выражение “ходить по кругу” когда-то означало “прогресс”?
8. Верите ли вы, что хорда в переводе с греческого означает “струна”?
9. Верите ли вы, что определение “касательной” уже есть в первом учебнике геометрии - “Начала” Евклида?
В Древней Греции круг и окружность считались венцом совершенства. Действительно в каждой своей точке окружность “устроена” одинаково, что позволяет ей как бы двигаться “по себе”. На плоскости этим свойством обладает еще лишь прямая. Одно из интереснейших свойств круга состоит в том, что он при заданном периметре ограничивает максимальную площадь.
В русском языке слово “круглый” тоже стало означать высокую степень чего-либо: “круглый отличник”, “круглый сирота” и даже “круглый дурак”.
Если вы когда-либо пробовали получить информацию от бюрократической организации, вас, скорее всего “погоняли по кругу”. Фраза “ходить по кругу” обычно не ассоциируется с прогрессом. Но в период индустриальной революции, выражение “ходить по кругу” очень точно отражало прогресс. Шкивы и механизмы давали машинам возможность увеличить производительность и значит сократить рабочую неделю.
Без понятия круга и окружности было бы трудно говорить о круговращении жизни. Круги повсюду вокруг нас. Окружности и циклы идут, взявшись за руки. Циклы получаются при движении по кругу. Мы изучаем циклы земли, они помогают нам разобраться, когда надо сажать растения и когда мы должны вставать.
Представление об окружности даёт линия движения модели самолёта, прикреплённого шнуром к руке человека, также обод колеса, спицы которого соответствуют радиусам окружности.
Термин “хорда” (от греческого “струна”) был введён в современном смысле европейскими учёными в XII-XIII веках.
Определение касательной как прямой, имеющей с окружностью только одну общую точку, встречается впервые в учебнике “Элементы геометрии” французского математика Лежандра (1752-1833 гг.). В “Началах” Евклида даётся следующее определение: прямая касается круга, если она встречает круг, но при продолжении не пересекает его.
2. Сформулируйте геометрические определения понятий, используя ключевые слова.
| № | рисунок | Определяемое понятие | Используемые ключевые понятия |
| 1 |
| Окружность | Точки плоскости, одинаковое расстояние, точка - центр. |
| 2 |
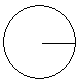
| радиус | Точки окружности, центр окружности, отрезок. |
| 3 |
| Хорда | Отрезок, точки окружности. |
| 4 |
| Диаметр | Хорда окружности, центр окружности. |
1. Что такое окружность?
Окружность – это фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки. Эта точка называется центром окружности)
2. Назовите элементы окружности. (радиус, хорда, диаметр, дуга)
3. Что такое радиус?
Радиус – отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.
4. Хорда.
Хорда – отрезок, соединяющий две точки окружности.
5. Диаметр.
Диаметр – отрезок, соединяющий две точки на окружности и проходящий через центр окружности.
6. Как связаны между собой диаметр и радиус окружности? (d = 2r)
3. Заполните таблицу
Сделайте вывод о взаимном расположении прямой и окружности, в зависимости от радиуса и расстояния от центра до прямой
| Радиус окружности меньше расстояния от центра окружности до прямой | Радиус окружности больше расстояния от центра окружности до прямой | Радиус окружности равен расстоянию от центра окружности до прямой |
| Прямая и окружность ………. | Прямая и окружность ………. | Прямая и окружность ………. |
Определение: Прямая, имеющая с окружностью две общие точки, называется секущей.
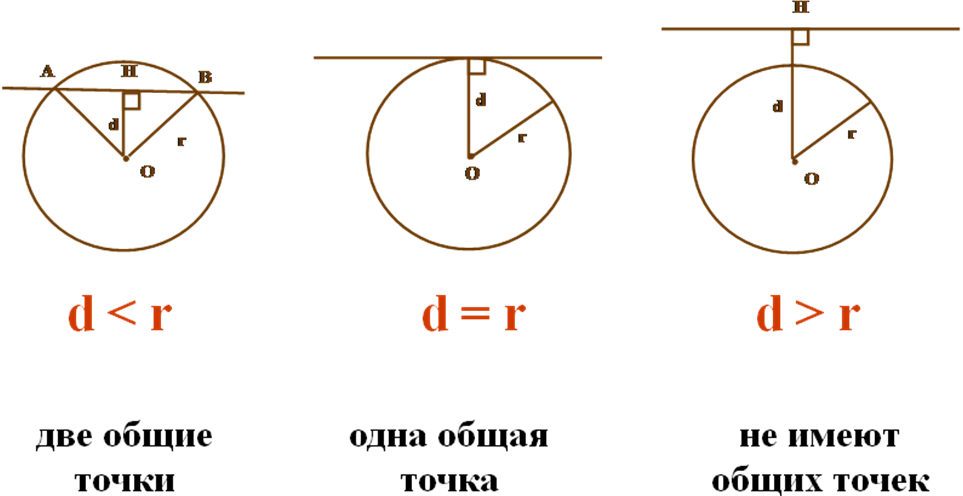
4. Задача. Устно.
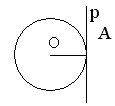
Каково взаимное расположение прямой p и окружности.
1) r = 12см, d = 9см: r d – прямая пересекает окружность в двух точках, является секущей;
2) r = 5,2см, d = 4,6см: r d – прямая p пересекает окружность в двух точках, является секущей;
3) r = 3,2дм, d = 3,7дм: r p не пересекает окружность;
4) r = 80мм, d = 14cм = 140мм: r p не пересекает окружность;
5) r = 6см, d = 0,6дм = 6см: r = d – прямая p – касательная.
III. Изучение нового материала. Касательная к окружности. Свойства касательной.
Мы показали, что прямая и окружность могут иметь одну или две общие точки и могут не иметь ни одной общей точки.
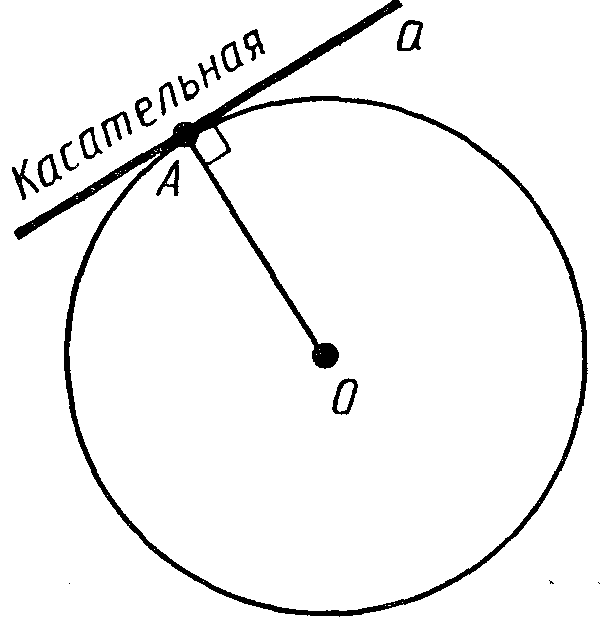
Прямая, имеющая с окружностью только одну общую точку. Называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Ребята, постройте, пожалуйста, радиус к точке касания. Вы заметили какую-нибудь особенность взаимного расположения этого радиуса и касательной? (если нет, то попросить воспользоваться угольником).
Формулируем теорему о свойстве касательной
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Докажем теорему о свойстве касательной и окружности.
Доказательства теоремы о свойстве касательной к окружности (см. п. 69, с. 166) лучше провести в ходе беседы учителя с учащимися по рис. 212, приготовленному на доске.
Наводящие вопросы:
- Предположим, что прямая р не перпендикулярна радиусу ОА.
Сравните расстояние от центра окружности до прямой р с радиусом окружности.
(Расстояние от точки О – центра окружности – до прямой р меньше радиуса, так как радиус ОА в данном случае является наклонной по отношению к прямой р, а как известно, любая наклонная больше перпендикуляра, проведённого из той же точки к той же прямой
что и наклонная.)
- Каково взаимное расположение прямой р и окружности? Почему?
- Может ли прямая р быть касательной к окружности? Объясни.
(Прямая р не может быть касательной к окружности, так как она имеет с ней две общие точки.)
- Верно ли предположение, что прямая р не перпендикулярна радиусу ОА? О чём говорит? (Предположение о том, что прямая р не перпендикулярна радиусу неверное, следовательно прямая р перпендикулярна радиусу.)
Теперь запишем это доказательство в тетради.
|
| Дано: окр. (О;r=ОА), р-касательная A к окружности, А-точка касания. Доказать: р Доказательство: |
Предположим, что р не ![]() ОА, тогда ОА наклонная к прямой р, а ОВ
ОА, тогда ОА наклонная к прямой р, а ОВ![]() р, т. к. ОВ ОА.
р, т. к. ОВ ОА.
IV. Закрепление нового материала
1. Решите задач
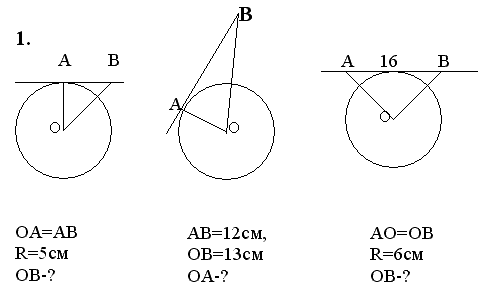
Задания выполняются на доске учащимися, учитель по необходимости помогает им.
V. Продолжение объяснения нового материала
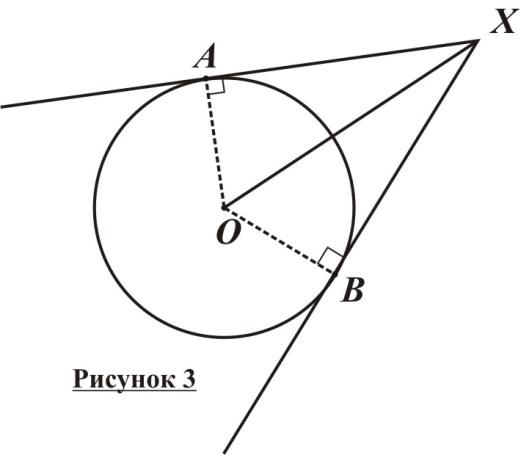
Ребята, а теперь постройте окружность и точку Р лежащую вне этой окружности.
Проведите через точку Р две касательные к окружности. Соедините центр окружности и точки касания отрезками.
 Р
Р
Ч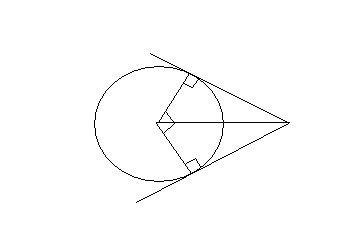 то вы можете сказать о отрезках РВ и РА ? Как луч РО делит
то вы можете сказать о отрезках РВ и РА ? Как луч РО делит 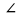 АРВ ?
АРВ ?
А вот как раз и это свойство
Откуда взять равенство этих элементов? Кто готов доказать нам этот факт.
Ученики сами доказывают данную теорему на доске и в тетради.
VII. Закрепление изученного. Решение задач
№ 635
635
Через точку А окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними.
Решение. ОА=ОВ=R, АВ=R (по условию), следует ∆АВС – равносторонний.
0, ∠ВАN = 900 – 600 = 300.
№ 637
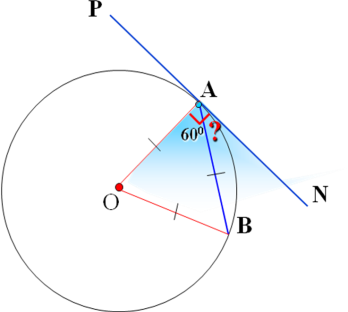
Угол между диаметром АВ и хордой АС равен 300. Через точку С проведена касательная, пересекающая прямую АВ в точке D. Докажите, что треугольник АСD – р авнобедренный.
авнобедренный.
Решение: ∆АОС – равнобедренный, т.к. ОС=ОА=R, значит 0.
D=O+OСD=300+900=1200 .
По свойству касательной ОС=R┴CD (касательная),
∆СDO – прямоугольный. 0.
0 – (A+ACD=1800 – (300+1200)=300.
0, следовательно ∆АСD – равнобедренный.
№ 638
638
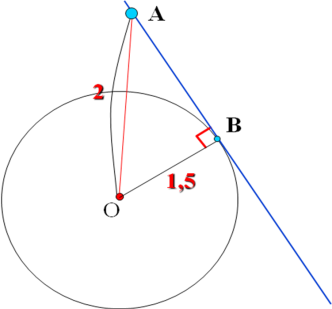
Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВ, если ОА = 2 см, а r = 1,5 см.
Решение. По свойству касательной АВ┴ОВ, следовательно ∆ОВА – прямоугольный.
По теореме Пифагора: АВ2 = ОА2 – ОВ2, 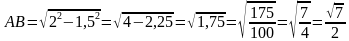 .
.
№ 639
П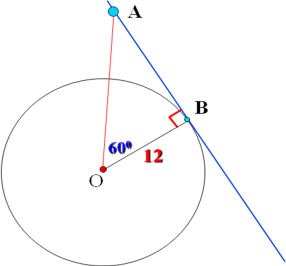 рямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВ, если угол АОВ равен 600, а r = 12 см.
рямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВ, если угол АОВ равен 600, а r = 12 см.
Решение.
По свойству касательной АВ┴ОВ, следовательно, ∆ОВА – прямоугольный.
∠ОАВ = 900 – 600 = 300. Отсюда АО = ОВ * 2 = 12 * 2 = 24 (см)
По теореме Пифагора: АВ2 = ОА2 – ОВ2,
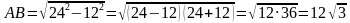 (см)
(см)
VII. Рефлексия
Каким свойством обладает касательная к окружности?
Сформулируйте теорему о двух касательных к окружности, проведенных из одной точки, лежащей вне этой окружности.
Возникали ли у вас трудности с усвоением сегодняшнего материала? И по какой причине?
VIII. Подведение итогов
На дом: п. 69, № 633, № 636.

 Получите свидетельство
Получите свидетельство Вход
Вход




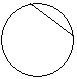
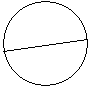









 Касательная к окружности, ее свойства. (274.38 KB)
Касательная к окружности, ее свойства. (274.38 KB)
 0
0 614
614 51
51 Нравится
0
Нравится
0


