Цели урока
Обучающие:
1) организовать деятельность учащихся по изучению различных случаев взаимного расположения двух окружностей;
создать условия для совершенствования навыков решения задач по теме «Окружность».
Развивающие:
1) совершенствовать умения логически мыслить и выражать свои мысли вслух;
2) стимулировать познавательную деятельность учащихся постановкой проблемного задания, оценкой и поощрением;
Воспитательные:
1) воспитывать у учащихся стремление к совершенствованию своих знаний;
2) воспитывать интерес к предмету.
Ход урока
1. Организационный момент.
Приветствие. Организация 5 групп по принципу «Кому нравится фигура…1) треугольник, 2) квадрат, 3) круг, 4) прямоугольник, 5) луч.
В каждой группе назначается модератор, ответственный за передачу результатов.
2. Мотивация урока
Как сказал древнегреческий философ Саади: “Ученик, который учится без желания - это птица без крыльев”.
И мне бы хотелось, чтобы у вас было желание учиться, узнавать что-то новое, неопознанное не только на сегодняшнем уроке, а всегда и только в этом случае своими “крыльями” будете “взлетать” все выше и выше.
А также мне очень хочется обратиться к словам известного российского математика А.И. Мордковича: “Кто с детских лет занимается математикой, этот развивает внимание, тренирует свой мозг, свою волю, воспитывает в себе настойчивость и упорство в достижении цели”.
3. Актуализация опорных знаний
Проведем опрос на повторение основных понятий. Каждая группа получила карточки с теоретическими вопросами. Ответ представляется каждой группой. Озвучиваются правильные варианты ответов и исправляются ошибки( ошибок в тесте 6).
Найдите ошибку:
Окружностью называется множество точек плоскости, равноудалённых от центра.
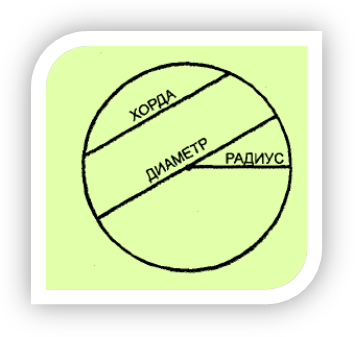
Радиус – это отрезок.
Отрезок, соединяющий две точки, окружности называется диаметром.
Хорда – часть диаметра.
Окружность называется описанной около треугольника, если она соединяет все его вершины.
Центр окружности, описанной около треугольника, является точкой пересечения медиан к стороне треугольника.
Прямая, проходящая через точку окружности перпендикулярно к диаметру, проведённому в эту точку, называется касательной.
Окружность называется вписанной в треугольник, если она касается всех его отрезков.
Центр окружности, вписанной в треугольник, является точкой пересечения его перпендикуляров.
Кроссворд
По горизонтали: 1. Множество точек плоскости, находящихся на одинаковом расстоянии от одной точки. 2.Часть окружности. 3.Отрезок, соединяющий центр окружности с какой-либо ее точкой. 4. Что в переводе с латинского означает слово диаметр.
По вертикали: 2.Отрезок, который соединяет две точки окружности и проходит через ее центр. 5.Точка, находящаяся на одинаковом расстоянии от всех точек окружности. 6.Часть плоскости, ограниченная окружностью. 7.Часть круга, ограниченная двумя радиусами. 8.Отрезок, соединяющий две точки окружности. 9. Как переводится на русский язык латинское слово радиус.
Повторение по слайдам свойств касательной, отрезка радиуса, перпендикулярного хорде.
4. Изучение нового материала
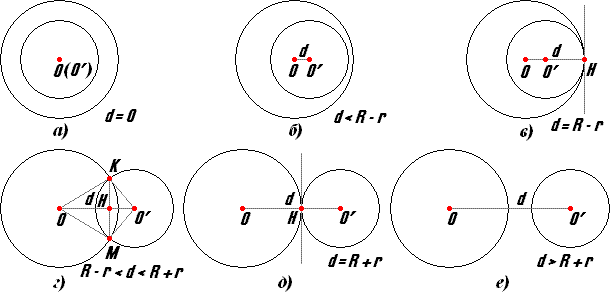
Перейдем к анализу возможных случаев расположения двух окружностей
а) Центры окружностей совпадают. Такие окружности называются концентрическими.
В случае равенства радиусов они совпадают. Если же радиусы этих окружностей не равны, то одна из них лежит внутри другой. Образуется фигура, которую называют кольцом.
б) Пусть теперь центры окружностей различны. Соединим их прямой, она называется линией центров данной пары окружностей.
Взаимное расположение окружностей будет зависеть только от соотношения между величиной отрезка d, соединяющего их центры, и величинами радиусов окружностей R,r.
1. Расстояние между центрами меньше разности радиусов: d>R-r (рис б).
2. Расстояние между центрами равно разности радиусов: d=R-r (рис в). Малая окружность лежит внутри большой, но имеет с ней общую точку на линии центров. Говорят, что имеет место внутреннее касание, а такие окружности называют внутренне касающимися.
Определение. Внутренне касающимися называют окружности, имеющие одну общую точку, причем центр меньшей из них расположен внутри большей.
Точка касания внутренне касающихся окружностей лежит на линии центров.
3. Расстояние между центрами больше разности радиусов, но меньше их суммы: R-r
Пересекающимися называют окружности, имеющие две общие точки.
4. Расстояние между центрами равно сумме радиусов: d=R+r (рис д)
Внешне касающимися называют окружности, имеющие одну общую точку, причем центр одной из них расположен за пределами второй.
Точка касания внешне касающихся окружностей лежит на линии центров.
5. Расстояние между центрами больше суммы радиусов: d>R+r
Физминутка для глаз.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Взаимное расположение двух окружностей (0.17 MB)
Взаимное расположение двух окружностей (0.17 MB)
 1
1 4618
4618 1101
1101 Нравится
0
Нравится
0








