Получите свидетельство
Вход
Как построить график
функции y=f(x+m)+n, если известен график
функции y=f(x)
Какая из формул задаёт:
- прямую пропорциональность;
-обратную пропорциональность;
-линейную функцию, график которой проходит через начало координат.
3)
2)
1)
5)
4)
2
2
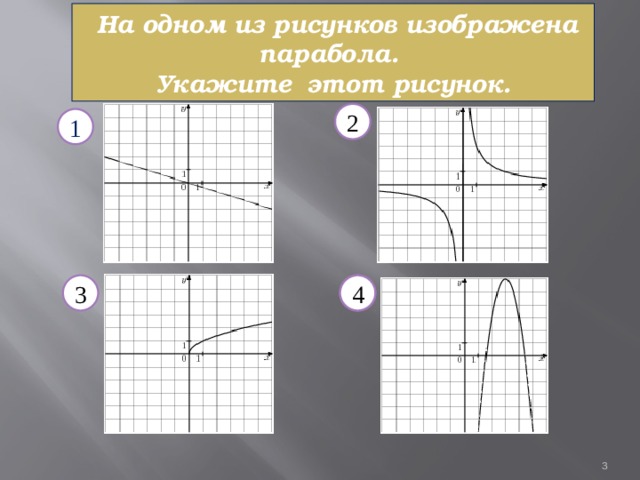
На одном из рисунков изображена парабола. Укажите этот рисунок.
2
1
3
4
4
2
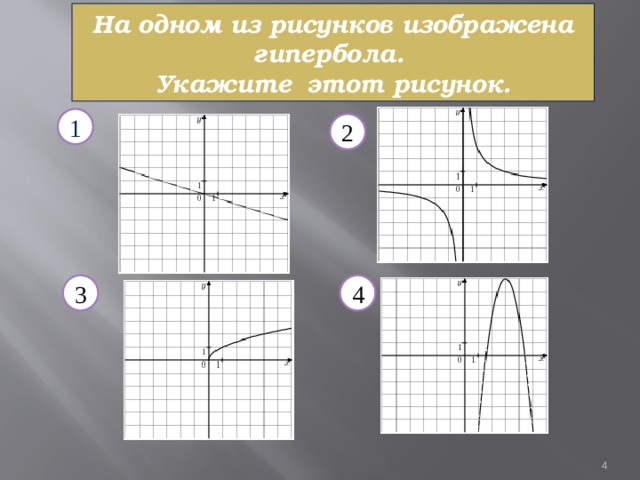
На одном из рисунков изображена гипербола. Укажите этот рисунок.
1
2
2
3
4
2
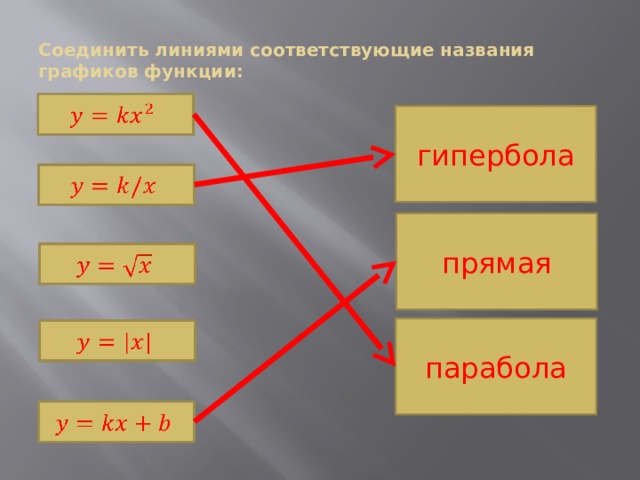
Соединить линиями соответствующие названия графиков функции:
гипербола
прямая
парабола
Соединить линиями соответствующие названия графиков функции:
гипербола
прямая
парабола
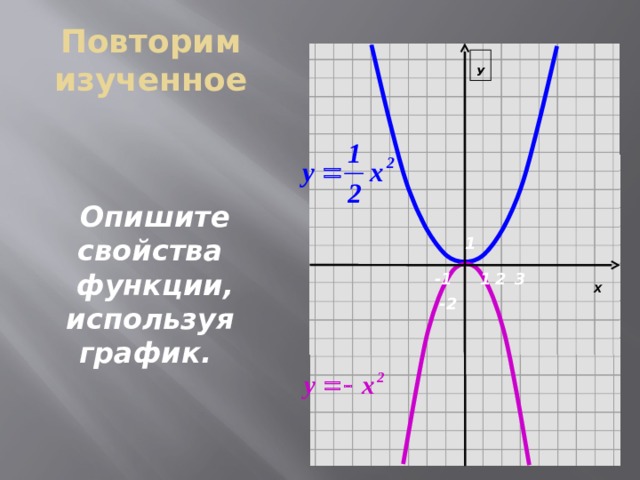
Повторим изученное
У
Опишите свойства
функции, используя
график.
1
3
-1
1
2
Х
-2
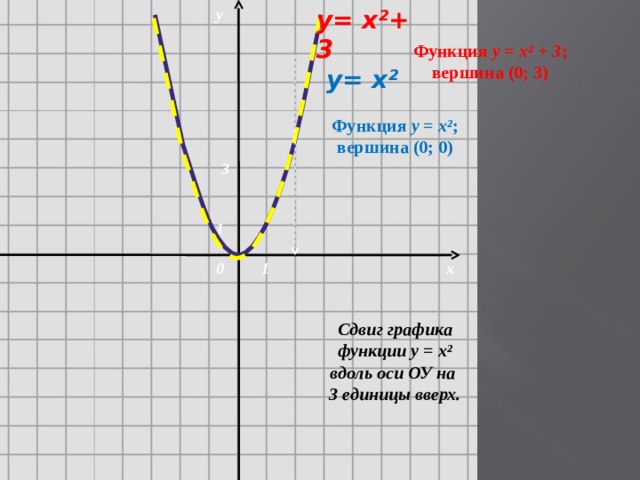
у= х ²+ 3
у
Функция у = х ² + 3 ; вершина (0; 3)
у= х ²
Функция у = х ² ; вершина (0; 0)
3
1
0
1
х
Сдвиг графика функции у = х ² вдоль оси ОУ на
3 единицы вверх.
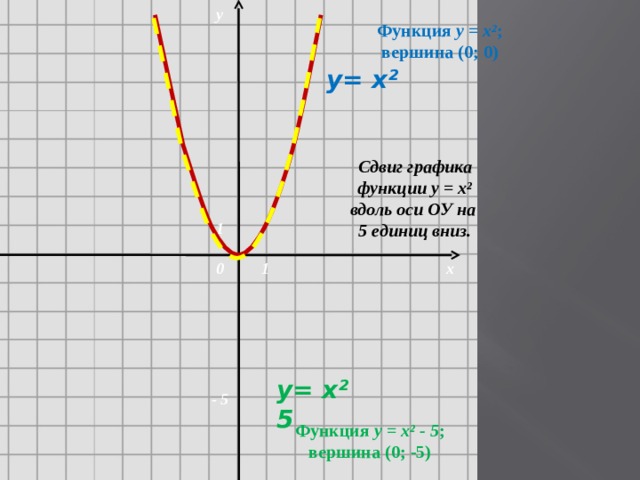
у
Функция у = х ² ; вершина (0; 0)
у= х ²
Сдвиг графика функции у = х ² вдоль оси ОУ на
5 единиц вниз.
1
1
0
х
у= х ² 5
- 5
Функция у = х ² - 5 ; вершина (0; -5)
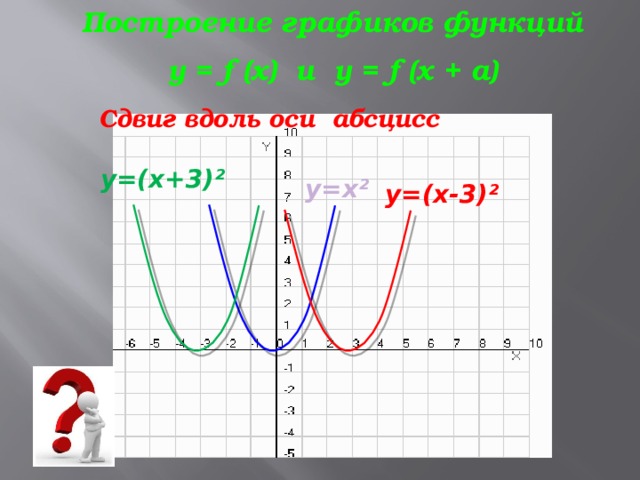
Построение графиков функций
y = f (x) и y = f (x + a)
Сдвиг вдоль оси абсцисс
y=(x+3) ²
y=x ²
y=(x-3) ²
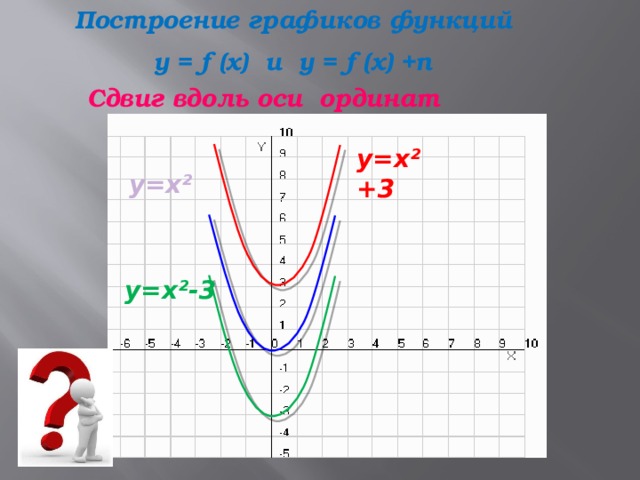
Построение графиков функций
y = f (x) и y = f (x) +n
Сдвиг вдоль оси ординат
y=x ²+3
y=x ²
y=x ²-3
0 и вправо , если m " width="640"
График функции График функции y = f(x + m) получается параллельным переносом графика функции y=f(x) вдоль оси х на |m| единиц масштаба влево, если m 0 и вправо , если m
0 и вниз , если n " width="640"
График функции График функции y = f(x)+n получается параллельным переносом графика функции y=f(x) вдоль оси y на |n| единиц масштаба вверх, если n 0 и вниз , если n
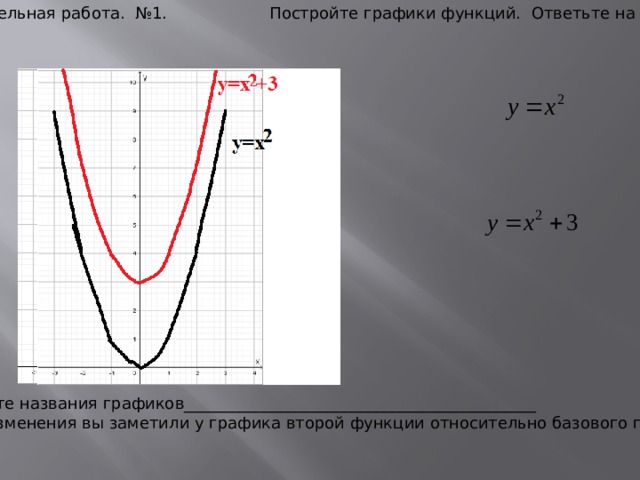
Самостоятельная работа. №1. Постройте графики функций. Ответьте на вопросы .
Запишите названия графиков____________________________________________
Какие изменения вы заметили у графика второй функции относительно базового графика?_________________________
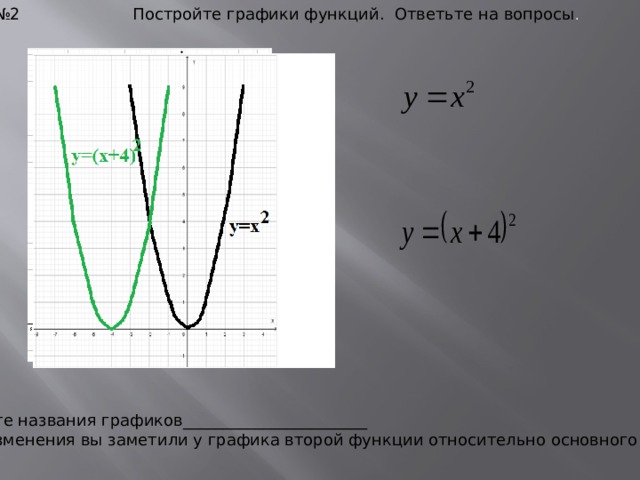
№ 2 Постройте графики функций. Ответьте на вопросы .
Запишите названия графиков_______________________
Какие изменения вы заметили у графика второй функции относительно основного графика?_____________
Выводы: основные преобразования графиков элементарных функций:
Сжатие и растяжение графика вдоль
оси y у=k f(x).
Преобразование симметрии относительно оси x у = - f(x)
Сдвиг вдоль оси абсцисс y = f (x + a)
Сдвиг вдоль оси ординат y = f (x) +n
2
вправо
3
вниз
5
в право
вверх
2
2
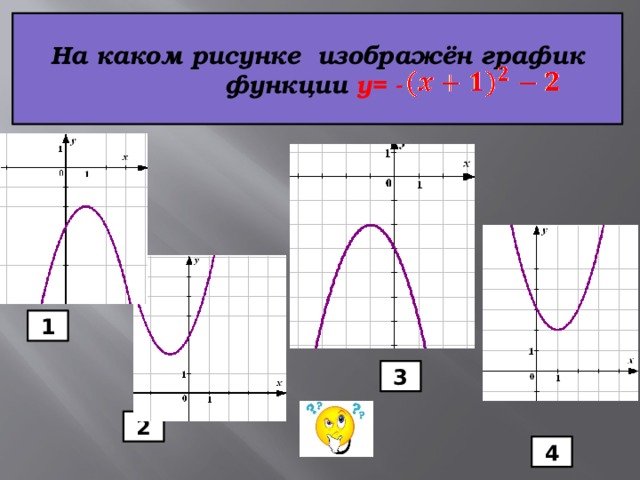
На каком рисунке изображён график
На одном из рисунков изображен график
функции
функции y= -
Укажите номер этого рисунка.
1
3
2
4
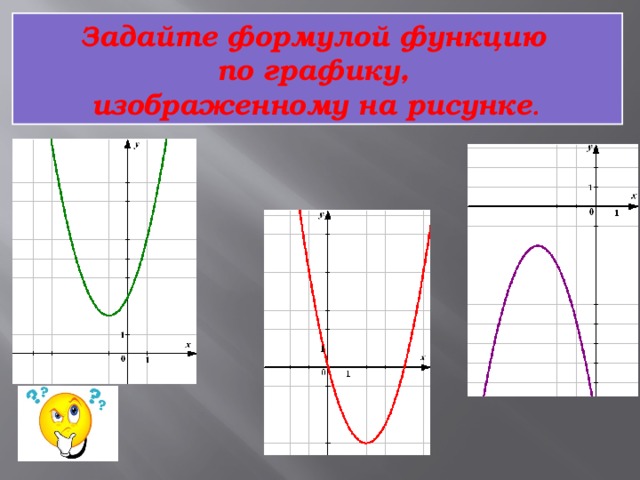
Задайте формулой функцию
по графику,
изображенному на рисунке .
Если нажать на прямоугольник «Подсказка» - переход на следующий слайд с разбором решения задания.
Если нажать на кнопку «Далее» - переход с следующему заданию.
2
Выберите из списка а)-г) формулу, задающую функцию, если ее график получен переносом графика функции влево вдоль оси абсцисс на 1 единицу и вверх вдоль оси ординат на 4 единицы: а) б) в) г)
2
0, и вправо, если m 1 5 0 1 x 5 ед. 3. Осуществить параллельный перенос полученного на втором шаге графика вдоль оси у на |n| единиц масштаба вверх, если n0, и вниз, если n Х=5 " width="640"
y
4 ед.
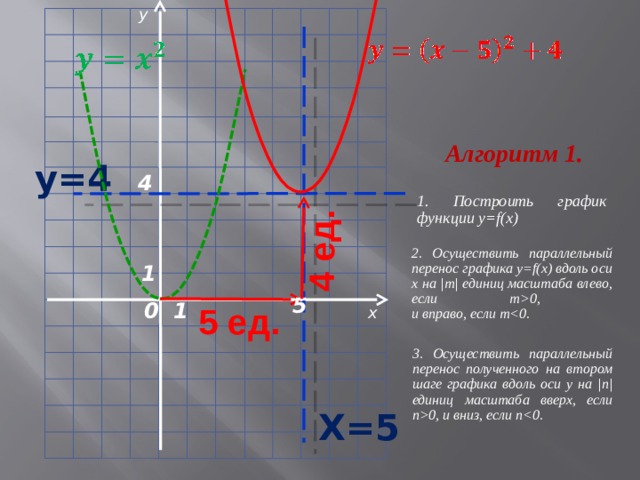
Алгоритм 1.
у=4
4
1. Построить график функции y=f(x)
2. Осуществить параллельный перенос графика y=f(x) вдоль оси х на |m| единиц масштаба влево, если m0, и вправо, если m
1
5
0
1
x
5 ед.
3. Осуществить параллельный перенос полученного на втором шаге графика вдоль оси у на |n| единиц масштаба вверх, если n0, и вниз, если n
Х=5
4 ед.
y
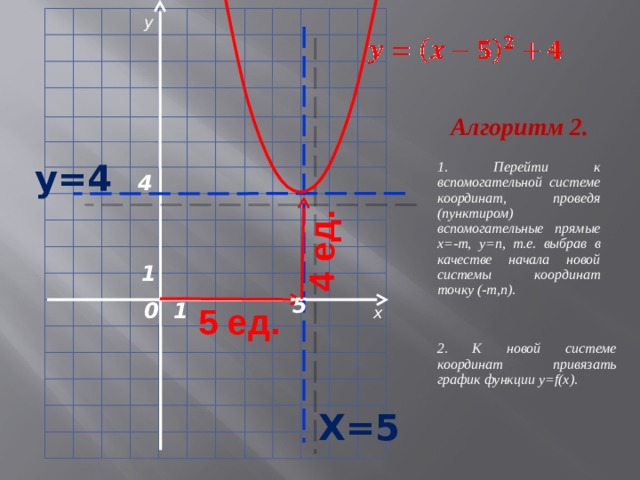
Алгоритм 2.
у=4
1. Перейти к вспомогательной системе координат, проведя (пунктиром) вспомогательные прямые х=-m, y=n, т.е. выбрав в качестве начала новой системы координат точку (-m,n).
4
1
5
0
1
x
5 ед.
2. К новой системе координат привязать график функции y=f(x).
Х=5
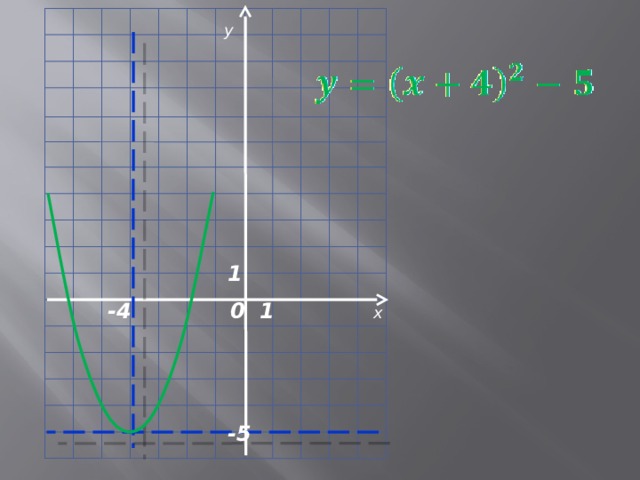
y
1
0
-4
1
x
-5
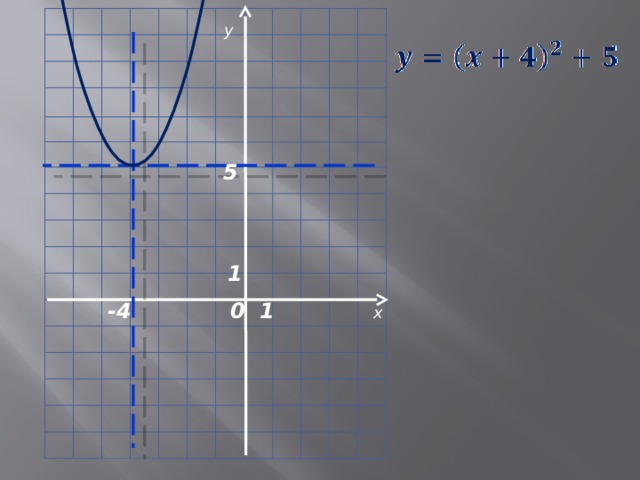
y
5
1
0
1
-4
x
y
1
5
0
1
x
-4
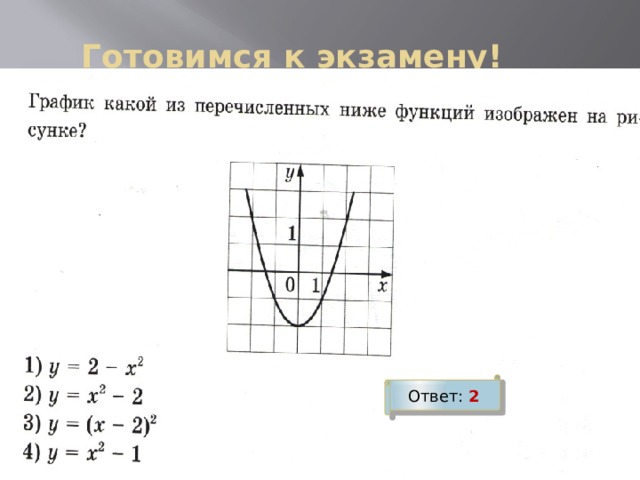
Готовимся к экзамену!
Ответ: 2
Готовимся к экзамену!
Ответ: 3
Как построить график... (1.87 MB)
0
299
73
Нравится
0
