МБОУ Алтунинская ООШ
Как подготовить
к успешной сдаче ОГЭ
по математике
Учитель математики
1 квалификационной категории
Рушева Т.Б.
Каждый учитель заинтересован в том, чтобы дать возможность ученикам получить качественную подготовку к экзамену по математике. В классах, где я работаю условно можно разделить ребят на тех, которые могут освоить математику, но не хотят; могут освоить математику, но необходимо долго и кропотливо трудиться; не могут освоить в силу своих способностей (ЗПР). Поэтому в своей работе стараюсь найти наиболее эффективные формы, методы и технологии обучения. Главная моя задача, чтобы выпускники успешно сдали единый государственный экзамен по математике.
При подготовке к итоговой аттестации всех учеников условно делю на следующие группы, состав которых может меняться:
1 группа - дети, требующие постоянной помощи.
2 группа - дети, способные справиться самостоятельно.
Участвуя в работе сетевого сообщества учителей математики познакомилась с учебно-методическим пособием «Не два на ОГЭ», подготовленным авторами Михаилом Исааковичем Альпериным и Сергеем Эрнестовичем Нохриным ГАОУ ДПО «Институт развития образования» г.Екатеринбурга.
Абсолютно согласна, с мнением авторов: «Если ученик, особенно слабый, не будет работать самостоятельно, написать экзаменационную работу на положительную оценку ему вряд ли удастся».
Авторы пособия предлагают:
Начинать работу по данной методике «Не два на ОГЭ» на заключительном этапе подготовки к ОГЭ (т.к. данный тип школьников, как правило, через неделю забывает всё, что изучал);
Регулярность занятий (задания выполняются школьником ежедневно);
Давать задания по 1-2 из различных тем;
Нельзя давать слишком много заданий, в идеале работа должна занимать не больше 10-15 минут, т.е. 5-6 заданий за один раз;
Задания каждому школьнику давать свои, чтобы ограничить списывание.
Данный метод подготовки к итоговой аттестации приемлем для школьников, не знающих и не желающих знать математику, т.е. как раз для школ, функционирующих в неблагоприятных условиях, там, где в классах обучаются ученики, для кого школа - это общение со сверстниками или отбывание времени, чтобы не ругали родители, либо это ученики с низким уровнем мотивации и ограниченными способностями.
Принципы данной методики я применяю при работе по подготовке к ОГЭ по математике учащихся, имеющих низкий, средний уровень подготовки.
Приведу пример применения методики «Не два на ОГЭ» по математике.
Обучающимся предлагается выполнить задание. К заданию прилагается ход решение, т.е. подсказки, какую теорию необходимо вспомнить, как последовательно ее применить. Выполняя каждый пункт предложенного порядка решения, ученик вспоминает теоретический материал и вырабатывает определенный алгоритм решения задания.
После выполнения всех заданий с подсказками предлагается еще несколько аналогичных, но уже для полного самостоятельного выполнения без конкретных путей решения.
Методику «Не два на ОГЭ» можно использовать для организации работы со слабоуспевающими учащимися не только в выпускных классах. Эта методика работает и для учащихся с разным уровнем подготовки в любом классе.
https://www.uchportal.ru/publ/23-1-0-9395
Применение образовательных технологий на уроках математики
Образовательные технологии - это совместная деятельность учащегося и педагога, это алгоритм действий педагога и детей в четко определенных условиях, который обеспечивает гарантированный образовательный результат.
Для достижения результата при планировании уроков я использую следующие технологии: карта понятий, карта памяти, фреймы (интеллект-карты). Эти технологии направлены на развитие умений анализировать, систематизировать информацию.
Карта понятий
Актуализация опорных знаний, умений и навыков - восполнить недостающие знания учащихся, вспомнить необходимые опорные знания.
Изображаем не схемы, а пишем слова. 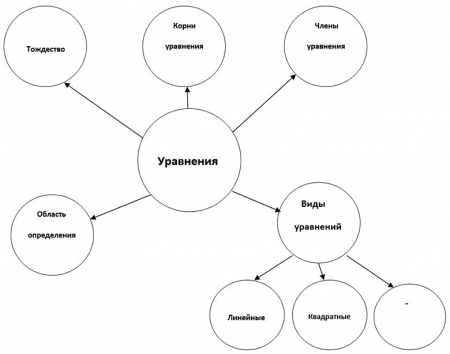
Основная идея, проблема или слово располагается в центре.
Главные ветви соединяются с центральной идеей, а ветви второго, третьего и т.д. порядка соединяются с главными ветвями.
Над каждой линией - ветвью пишется только одно ключевое слово.
Данная технология позволяет эффективнее решать образовательные задачи:
поиск информации;
формирование понятий и установление связей между ними;
классификация, систематизация и обобщение.
Например: 1) алгебра - решение задания 11 по теме "Графики функций".
Карта памяти
С помощью карт очень легко готовиться к экзаменам и зачетам. В своей работе использую прием "Разработка заданий массивом" из банка заданий для подготовки к ОГЭ.
Карта памяти:
углубляет понимание;
позволяет хранить информацию в свернутом виде, а при необходимости разворачивать;
позволяет оценивать информацию с разных точек зрения и фиксировать ключевые моменты;
помогает вспомнить детали, связанные с ключевыми моментами
Задание № 19 ОГЭ по математике "Анализ геометрических высказываний"
1. Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: 1; 2.
2. Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: 2; 3.
3. Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведенная из вершины, противолежащей основанию, делит основание на две равные части.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: 1; 3.
4. Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов любого треугольника равна 180°.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: 1; 3.
5. Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудаленные от заданной точки, лежат на одной окружности.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: 2; 3.
6. Укажите номера верных утверждений.
1) Если три стороны одного треугольника пропорциональны трем сторонам другого тре-угольника, то треугольники подобны.
2) Сумма смежных углов равна 180°.
3) Любая высота равнобедренного треугольника является его биссектрисой.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: 1; 2.
Фреймы (интеллект-карты)
Мыслим ассоциативно, выстраивая из полученной информации взаимосвязи мыслей и логическую структуру, а затем появляется образ.
Приемы работы
Обучающийся:
отвечает на вопросы;
формулирует вопросы;
подписывает элементы в схеме;
составляет связный текст по схеме.
Задания множественного выбора

геометрическая фигура;
четырехугольник;
прямоугольник;
ромб.

геометрическая фигура;
четырехугольник;
прямоугольник;
трапеция.
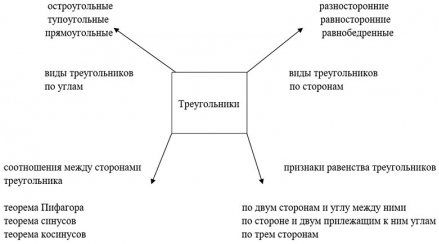
Например: геометрия - решение задач на решетке ( нахождение площадей геометрических фигур.
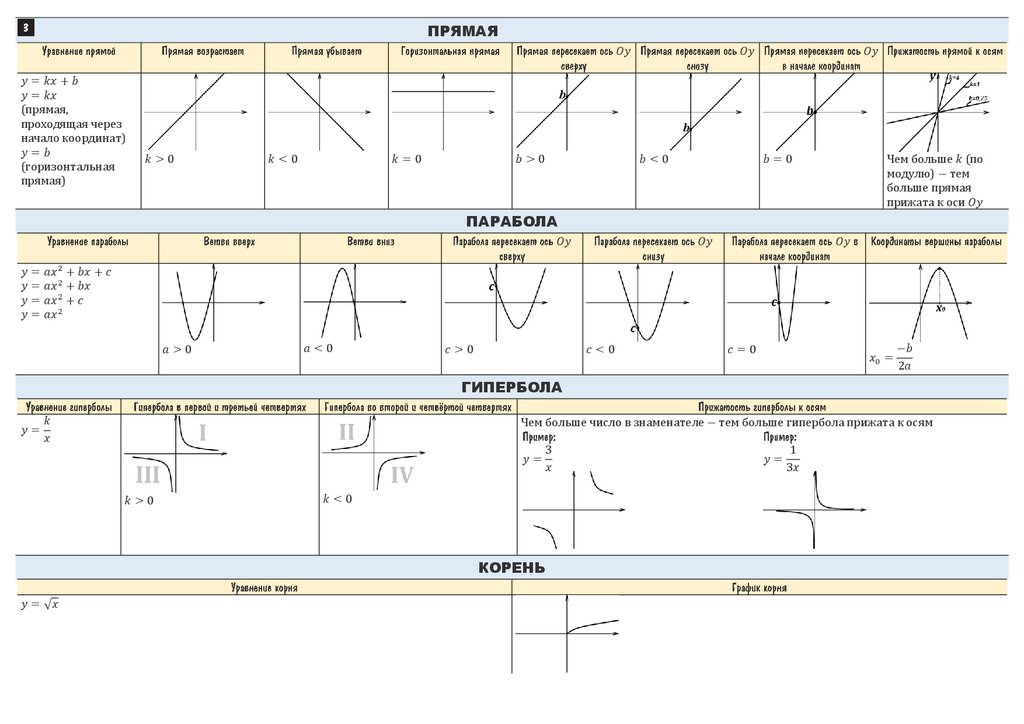
Задание 11. Графики функций
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
Коэффициенты
А) k
Б) k0
В) k0, b
Графики
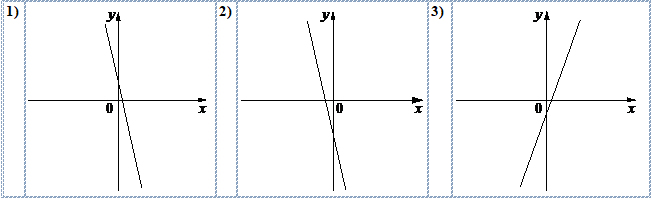
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В |
|
|
|
|
Прием «Задание массивом»
Любой из трех уровней домашнего задания учитель может задавать массивом, т.е. предлагает большое количество упражнений, вопросов, задач, из которых ученик может выполнить столько, сколько посчитает нужным, или не менее определенного количества. Например, учитель дает десять задач (или, скажем стихов), из которых ученик должен сам выбрать и решить (выучить) не менее заранее оговоренного минимального объема задания(приложение)
Важный психологический эффект: самостоятельный выбор задания дает дополнительную возможность самореализации, ведь известно, как этого не хватает ученикам в условиях нашей школы, особенно в подростковом возрасте. А учебный предмет, в свою очередь, становится им интереснее.
Из массива заданий ученик выбирает тот уровень сложности, на который способен «замахнуться». Таким образом, он сам отслеживает уровень своей компетентности.
Преимущества задания массивом:
1) происходит самосогласование ребенка и уровня задач, которые он решает, он учится с первого взгляда оценивать сложность задачи;
2) дети решают разные задачи, у них появляется дополнительная возможность обменяться решениями;
3) выбирая свои задачи, ученик читает остальные, его учебный кругозор становится шире, он знает гораздо больше задач, чем ему предлагают.
Приложение1
Шпаргалка. Дробные числа и действия над ними.
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.
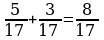
Чтобы из одной дроби вычесть другую дробь с таким же знаменателем, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тем же.
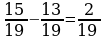
Сократить дробь - означает разделить ее числитель и знаменатель на одно и то же число (не равное нулю). В результате получаем равную (эквивалентную) дробь, но с меньшими числителем и знаменателем
Чтобы сократить дробь, нужно последовательно проверять, на что делятся числитель и знаменатель. Если находятся общий делитель, то на него и сокращать
Если разложить числитель и знаменатель на множители, то это упростит сокращение
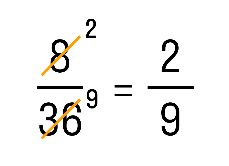
Пример. Сократим обыкновенную дробь 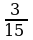
Разделим числитель и знаменатель на общий делитель 3.
3 : 3 =1; 15 : 3 = 5
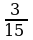 =
= 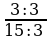 =
= 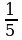

Приведение дробей к общему знаменателю.
Чтобы привести дроби к общему знаменателю, надо:
1)подобрать наименьший общий знаменатель;
2)разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель;
3)умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Например: 1) Приведите дробь ![]() к знаменателю 35.
к знаменателю 35.
Ч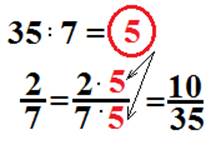 исло 35 делится на 7 без остатка. Значит, это преобразование возможно. Найдем дополнительный множитель. Для этого разделим 35 на 7. Получим 5. Умножим на 5 числитель и знаменатель исходной дроби.
исло 35 делится на 7 без остатка. Значит, это преобразование возможно. Найдем дополнительный множитель. Для этого разделим 35 на 7. Получим 5. Умножим на 5 числитель и знаменатель исходной дроби.
2) Приведите дробь ![]() к знаменателю 18.
к знаменателю 18.
Н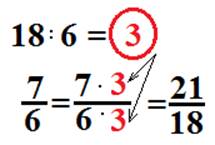 айдем дополнительный множитель. Для этого разделим новый знаменатель на исходный. Получим 3. Умножим на 3 числитель и знаменатель данной дроби.
айдем дополнительный множитель. Для этого разделим новый знаменатель на исходный. Получим 3. Умножим на 3 числитель и знаменатель данной дроби.
3) Приведите дроби к общему знаменателю 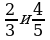
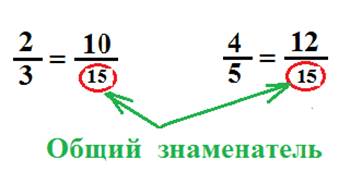
Дробь ![]() можно привести к знаменателю 15 и дробь
можно привести к знаменателю 15 и дробь ![]() можно привести к знаменателю 15. У дробей
можно привести к знаменателю 15. У дробей ![]() и
и ![]() общий знаменатель 15.
общий знаменатель 15.
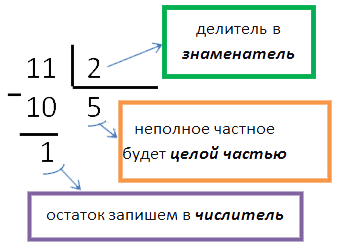
Чтобы выделить из неправильной дроби целую часть, надо числитель разделить на знаменатель. Если числитель разделился с остатком, то неполное частное будет целой частью смешанного числа, а остаток - числителем дробной части. Знаменатель останется прежним.
Например: выделить целую часть из неправильной дроби 
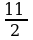 , разделим в столбик числитель на знаменатель
, разделим в столбик числитель на знаменатель
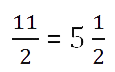
Чтобы представить смешанное число в виде неправильной дроби надо:
Умножаем целую часть на знаменатель 3 · 5 = 15
Прибавляем числитель 15 + 2 = 17
З![]() аписываем полученную сумму в числитель новой дроби, а знаменатель оставляем прежним.
аписываем полученную сумму в числитель новой дроби, а знаменатель оставляем прежним.
Умножение обыкновенной дроби на дробь
числитель первой дроби умножить на числитель второй дроби и их произведение записать в числитель новой дроби;
знаменатель первой дроби умножить на знаменатель второй дроби и их произведение записать в знаменатель новой дроби;
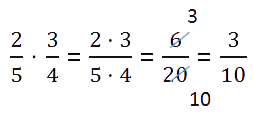
(Прежде чем перемножать числители и знаменатели проверьте нельзя ли сократить дроби. Сокращение дробей при расчётах значительно облегчит ваши вычисления).
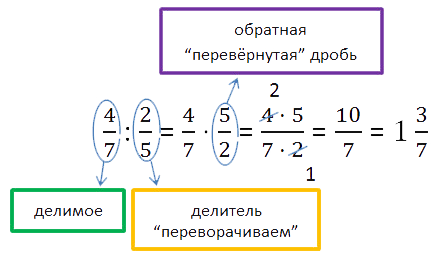
Деление дроби на дробь.
Чтобы разделить одну обыкновенную дробь на другую, отличную от нуля, нужно:
числитель первой дроби умножить на знаменатель второй дроби и записать произведение в числитель новой дроби;
знаменатель первой дроби умножить на числитель второй дроби и записать произведение в знаменатель новой дроби.
Умножение, деление смешанных чисел
Чтобы выполнить умножение, деление смешанных чисел , надо вначале превратить их в неправильные дроби и после этого умножить( разделить) по правилу умножения ( деления) обыкновенных дробей.
Например:
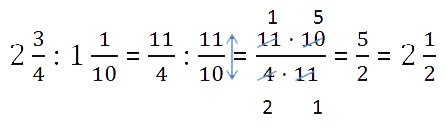
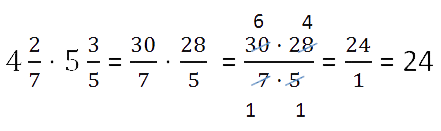 2)
2)
Сложение и вычитание десятичных дробей.
При сложении (вычитании) десятичные дроби записываются «столбиком», так чтобы одноимённые разряды находились друг под другом без смещения. При этом запятые должны стоять чётко друг под другом.
Неправильная запись

Правильная запись

Складывают десятичные дроби в столбик как натуральные числа, не обращая внимания на запятые.
В ответе запятую ставим под запятыми в исходных дробях.
Например:
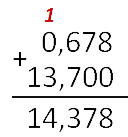
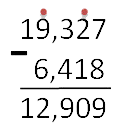
Умножение десятичных дробей происходит в три этапа.
Десятичные дроби записывают в столбик и умножают как обыкновенные числа.
Считаем количество знаков после запятой у первой десятичной дроби и у второй. Их количество складываем.
В полученном результате отсчитываем справа налево столько же цифр, сколько получилось их в пункте выше и ставим запятую.
Например:
![]()
(Записываем десятичные дроби в столбик и умножаем их как натуральные числа, не обращая внимания на запятые. То есть 3,11 мы рассматриваем как 311, а 0,01 как 1).
![]()
Получили 311. Теперь считаем количество знаков (цифр) после запятой у обеих дробей. В первой десятичной дроби два знака и во второй - два. Общее количество цифр после запятых: 2 + 2 = 4
Отсчитываем справа налево 4 знака (цифры) у полученного числа. В полученном результате цифр меньше, чем нужно отделить запятой. В таком случае нужно слева приписать недостающее число нулей.
У нас не хватает одной цифры, поэтому приписываем слева один ноль.

Деление десятичных дробей друг на друга
Определяем дробь с наибольшим количеством знаков (цифр) справа от запятой.
Умножаем обе десятичные дроби на 10, 100, 1000 и т.д., чтобы превратить десятичные дроби в целые числа.
Делим обыкновенные числа по правилам деления в столбик и записываем ответ.
Н![]() апример:
апример:
Наибольшее количество знаков (цифр) после запятой у первой десятичной дроби, поэтому ориентируемся на неё. Чтобы превратить 7,44 в целое число нужно умножить его на 100 (cм. умножение десятичных дробей).
На 10, 100, 1000 и т.д. умножаются обе десятичные дроби.
И умножаются они на одно и то же число. То есть, если вы умножили первую дробь на 10, то и вторую вы должны умножить на 10.
(7,44 · 100) : (0,4 · 100) =
Умножаем каждую из десятичных дробей на 100.
(7,44 · 100) : (0,4 · 100) = 744 : 40 =
Делим обыкновенные числа в столбик и записываем ответ. Помним, что изначально мы делили десятичные дроби.
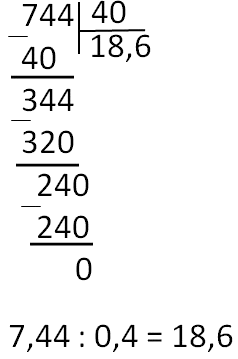
Карточка 1
Выполните сложение и вычитание дробей с одинаковыми знаменателями.
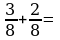 ; 2)
; 2) 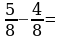
Выполните сокращение дробей.
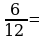
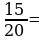
Выполните сложение и вычитание дробей с разными знаменателями.
5) 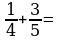
6) 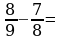
Выделите целую часть из неправильной дроби.
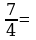
8)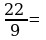
Представьте смешанное число в виде неправильной дроби.
9) 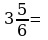
10)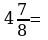
Выполните умножение, деление дробей.
11)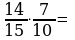
12) 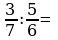
Выполните умножение, деление смешанных чисел.
13) 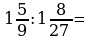
14) 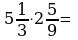
Карточка 2
(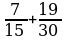 )
)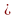
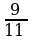 =
=
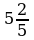 : (
: ( 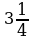 -
- 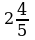 ) =
) =


 Получите свидетельство
Получите свидетельство Вход
Вход












 Как подготовить к успешной сдаче ОГЭ по математике (576.23 KB)
Как подготовить к успешной сдаче ОГЭ по математике (576.23 KB)
 0
0 37
37 0
0 Нравится
0
Нравится
0


