Исследование золотого сечения

Исследование золотого сечения

Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора, а другое - деление отрезка в среднем и крайнем отношении … Первое можно сравнить с мерой золота ; второе же больше напоминает драгоценный камень

Окружающий нас мир многообразен….

Людей с давних времён волновал вопрос, подчиняются ли такие неуловимые вещи как красота и гармония, каким либо математическим расчётам.

Можно ли «проверить алгеброй гармонию?» – как сказал А.С. Пушкин.

Конечно, все законы красоты невозможно вместить в несколько формул, но, изучая математику, мы можем открыть некоторые слагаемые прекрасного.

Теорему Пифагора знают многие люди, а вот что такое «золотое сечение» – далеко не все. Расскажем вам об этом “драгоценном камне”.

Что же такое золотое сечение? Рассмотрим отрезок АВ.

Его можно разделить точкой С на две части бесконечным множеством способов, но говорят что точка С производит золотое сечение отрезка АВ, если выполняется пропорция: длина меньшего отрезка так относится к длине большего, как больший отрезок относится к длине всего отрезка, т.е.

Термин золотое сечение ввёл в XVI веке великий художник, учёный и изобретатель Леонардо да Винчи. В истории утвердились три варианта названия: золотое сечение, золотая пропорция и третье – деление отрезка в среднем и крайнем отношениях. Кроме того, золотое сечение награждали эпитетами «божественное», «чудесное», «превосходнейшее», потому что-то, где оно присутствует, вызывает у нас ощущение красоты и гармонии.

Деление отрезка в золотом отношении

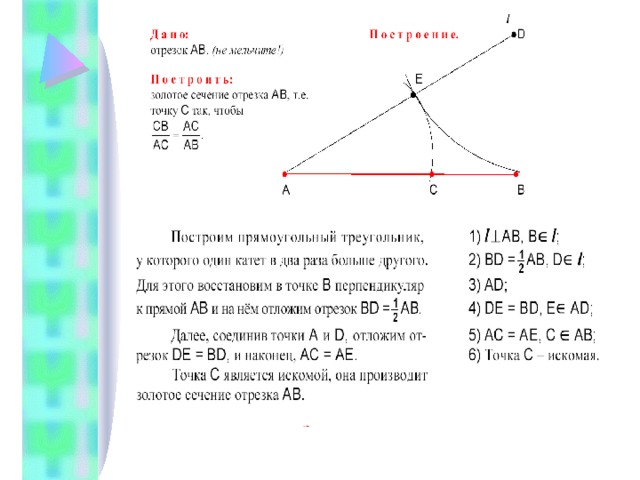
Отношение длины меньшего отрезка к длине большего отрезка и отношение большего к длине всего отрезка равно 0,62. Такое отношение и будет золотым. Полученное число обозначается буквой . Это первая буква в имени великого древнегреческого скульптора Фидия, жившего в V в до н.э., который часто использовал золотое отношение в своих произведениях.

Прямоугольник, стороны которого находятся в золотом отношении, т.е.

отношение ширины к длине даёт число , называется золотым прямоугольником .

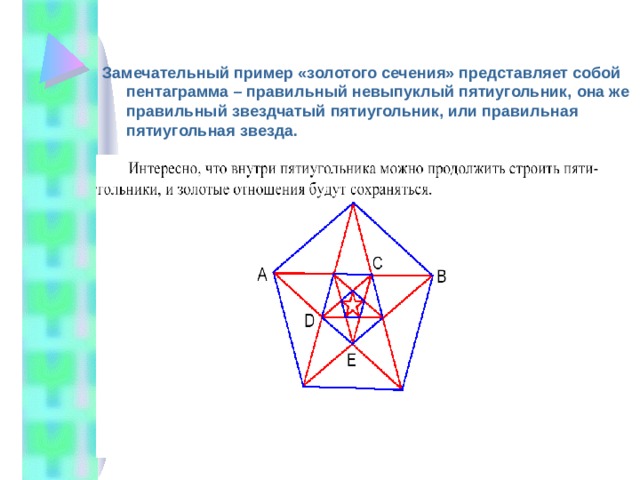
Замечательный пример «золотого сечения» представляет собой пентаграмма – правильный невыпуклый пятиугольник, она же правильный звездчатый пятиугольник, или правильная пятиугольная звезда.

На этой знаменитой картине И. И. Шишкина с очевидностью просматриваются мотивы золотого сечения. Ярко освещенная солнцем сосна (стоящая на первом плане) делит длину картины по золотому сечению. Справа от сосны - освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. Слева от главной сосны находится множество сосен - при желании можно с успехом продолжить деление картины по золотому сечению и дальше .

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V век до н.э.).

Строительством храма Парфенон руководил архитектор Фидий .

длины здания Парфенона в Афинах к его высоте равно

КВ: АВ = СВ :АС= АВ:ВС=

Отношение

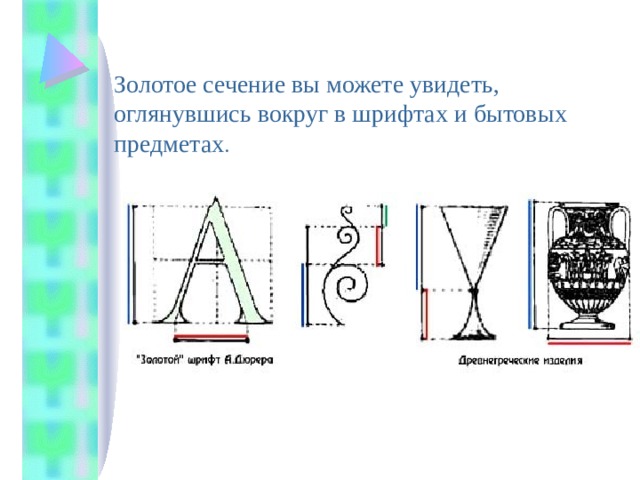
Золотое сечение вы можете увидеть,

оглянувшись вокруг в шрифтах и бытовых

предметах .

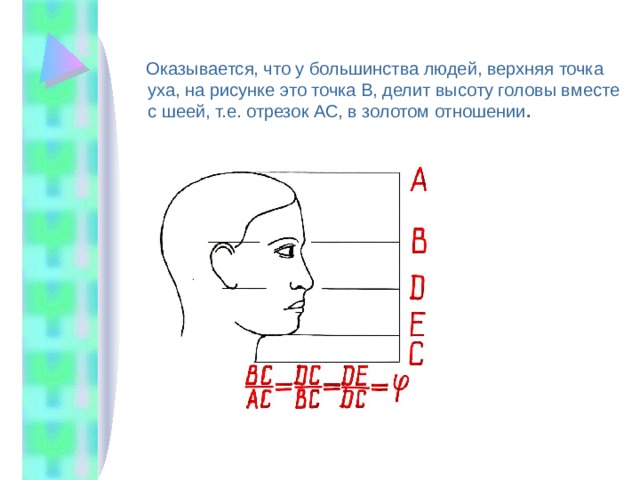
Оказывается, что у большинства людей, верхняя точка уха, на рисунке это точка В, делит высоту головы вместе с шеей, т.е. отрезок АС, в золотом отношении .

«Золотое сечение» в архитектуре Вышнего Волочка

Механико-технологический техникум.

АВ = 217мм

АС = 84мм

СВ = 133мм

АС : СВ = 84 : 133 ≈ 0,6

СВ : АВ = 133 : 217 ≈ 0,6

АС : СВ = СВ : АВ

Здесь есть золотое сечение .

Казанский собор .

АВ = 171мм

АС = 67мм

СВ = 104мм

АС : СВ = 67 : 104 ≈ 0,6

СВ : АВ = 104 : 171 ≈ 0,6

АС : СВ = СВ : АВ

Здесь есть золотое сечение.

Театр.

АВ = 50 мм

АС = 19 мм

СВ = 31 мм

АС : СВ = 19 : 31 ≈ 0,6

СВ : АВ = 31 : 50 ≈ 0,6

АС : СВ = СВ : АВ

АВ = 93 мм

АС = 33 мм

СВ = 60 мм

АС : СВ = 33 : 60 ≈ 0,6

СВ : АВ = 60 : 93 ≈ 0,6

АС : СВ = СВ : АВ

Здесь есть золотое сечение .

Предметы и явления, которым свойственна мера, целесообразность и гармония воспринимаются как красивое и вызывают у нас чувство восхищения, радости, поднимают настроение.

В этом состоит секрет того могучего эмоционального воздействия, которое эти здания оказывают на зрителя.

В данной работе описано применение «золотого сечения» только на нескольких зданиях, но здания, при построении которых применяли «золотое сечение», встречаются в нашем городе неоднократно.