Построение правильных многоугольников. Решение задач повышенной сложности

( Урок посвящается юбилею со дня рождения А.С. Пушкина )

Цель урока: научиться строить правильные десятиугольник и      пятиугольник.

Задачи урока:

- закрепить знания учащихся по построению правильных многоугольников;

- преодолеть в сознании учеников представление о « сухости» предмета, оторванности от жизни и практики;

- показать красоту  решения задач на построение с помощью циркуля и линейки;

- показать связь геометрии с литературой, философией,музыкой,искусством.

                                Ход урока.

Учитель: Здравствуйте, ребята! Сегодня у нас необычный урок математики. Мы посвящаем этот урок юбилею со дня рождения А.С.Пушкина.

Под музыку Г.Свиридова  звучат отрывки из стихотворений великого поэта А.С.Пушкина « Я помню чудное мгновенье», «Бахчисарайский фонтан», «Зимнее утро». По окончании чтения стихов пара девятиклассников исполняют вальс.

Учитель:  Конечно вы все узнали автора прозвучавших строк. Да. Именно А.С. Пушкин. Пушкин – великий поэт, имя которого известно всему миру, юбилей которого отмечается в июне этого года.  Прислушайтесь  к себе, к своему душевному состоянию. Вам понравилось? А кто почувствовал радость в душе от созвучия  музыки и человеческих движений? Можете объяснить?

Когда созвучны - -это значит гармоничны, это значит красивы.

Учитель:    Я предлагаю вашему вниманию  строки из воспоминаний И.Кеплера и  прошу подумать над тем, по какому случаю звучит восторг в его словах?

«Восемь месяцев назад предо мной блеснул первый луч света, за три месяца увидел я день и наконец, совсем недавно я смог увидеть лучезарное солнце… Я похитил золотые сосуды египтян, чтобы создать из них храм моему божеству вдали от пределов Египта… Жребий брошен. Я пишу свою книгу. Прочтётся ли она  моими современниками или потомством - мне всё равно – она найдёт своего читателя. Разве Господь Бог не ждал шесть тысяч лет созерцателя своего творенья?»

Вместе с учащимися выясняем, что зрелище, представшее перед ним – Вселенная, хранящая множество тайн. И одна из них в результате титанического труда Кеплера вдруг открылась ему. Теперь она известна всему культурному миру как третий Закон  Кеплера: КВАДРАТ ОТНОШЕНИЯ ПЕРИОДОВ ДВУХ ПЛАНЕТ РАВЕН КУБУ ОТНОШЕНИЯ ДЛИН БОЛЬШИХ ПОЛУОСЕЙ ИХ ОРБИТ.

 Учитель: Можно спросить: «А что ему орбиты, чтобы так ликовать?». Ответ находим у другого мыслителя, Эйнштейна.

«Ощущение тайны – наиболее прекрасное из доступных нам переживаний. Именно это чувство стоит у колыбели истинного искусства и настоящей науки».

Учитель: Как видим восторгаться можно открытиями, стихами, танцами, музыкой…  А можно ли испытывать эти чувства восторга, красоты, восхищения при изучении математики?... Безусловно. Именно красивым, более совершенным всегда считалось решение задач на построение, если оно содержит как можно меньше этапов построения. Вообще, задачи на построение чрезвычайно содержательны в математическом и логическом отношении. Это настоящие математические исследования в миниатюре. Начнём с самой окружности, являющейся основным элементом при решении задач на построение. Окружность самая простая из всех кривых линий, в тоже время самая древняя и таинственная геометрическая фигура. Древние философы  придавали окружности огромное значение. По Аристотелю, вся небесная материя, т.е. звёзды, планеты, могут вращаться только по окружности, как по самой совершенной линии. Эта теория просуществовала несколько столетий. Окружность является симво-лом многих явлений, предметов, состояний.

Ну и естественно, деление окружности на равные части для  построения правильных многоугольников имело важное значение для пифагорейцев, которые утверждали, что число лежит в основе всех явлений мира.

Учитель: Вспомним, какие правильные многоугольники мы уже научились строить.

Учащиеся: Правильный треугольник, правильный четырёхугольник, правильный шестиугольник и т.д. (Ученики строят фигуры с помощью циркуля и линейки).

Учитель: На сегодняшнем уроке мы рассмотрим задачи повышенной трудности.

№1210 («Геометрия,7-9», Л.С.Атанасян).

Впишите в окружность правильный десятиугольник.

Учащийся : При решении этой задачи я предлагаю воспользоваться свойством стороны правильного десятиугольника, а именно,  сторона правильного десятиугольника равна большей части радиуса, разделённого в отношении золотого сечения. (Учащиеся строят правильный десятиугольник).

Далее ученик коротко сообщает о том, что термин «золотое сечение» ввёл известный художник Леонардо да Винчи. Он назвал золотым сечением деление отрезка таким образом, что отношение всего отрезка к большей части равно отношению его большей части к его меньшей части. В эпоху Возрождения золотое сечение было очень популярно среди художников, архитекторов, скульпторов. В большинстве живописных пейзажей линия горизонта делит полотно по высоте в отношении золотого сечения. А выбирая размеры самой картины старались, чтобы отношение ширины к высоте тоже равнялось отношению золотого сечения. Такой прямоугольник  стали называть «золотым». Бывает и «золотой треугольник». Это  равнобедренный треугольник, у которого в отношении золотого сечения находятся длина боковой стороны и основания треугольника. «Золотой» треугольник использовал Леонардо да Винчи в композиции картины «Джоконда». А вот что сказал о золотом сечении И.Кеплер:

«Геометрия владеет двумя сокровищами: 1) теорема Пифагора; 2)деление отрезка  в крайнем и среднем отношении.  Первое можно сравнить с мерой золота, второе же больше напоминает драгоценный камень».

Учащийся: Пятиконечная звезда – пентаграмма всегда привлекала внимание людей совершенством формы. Пифагорейцы именно её выбрали  символом своего союза. Она же считалась амулетом здоровья. Пентаграмму никто не изобретал, её только копировали с натуры. Вид пятиконечной звезды имеют пятилепестковые цветы плодоносных деревьев и кустарников, морские звёзды. Те и другие создания природы человек наблюдает уже тысячи лет. Знак пятиконечной  звезды уходит своими корнями в Месопотамию. Он был впервые обнаружен  при раскопках  древнего Вавилона. Это был геометрический знак пяти планет (Юпитера,Сатурна,Меркурия, Марса,Венеры). Знак пентаграммы всегда употреблялся в виде защитного орудия против нападения злых, враждебных сил и являлся средством покорения их.

Учащийся: Используя пентаграмму, можно расшифровать информацию ноты «ДО». Нота связана с основой жизненного начала в материальном мире. Слово «ДО» указывает на то , что мы, будучи творцами , должны сами потроить дом в мироздании, где буква «Д» символизирует дом, а буква «О»  - мир, мироздание.

Весь материал - смотрите документ.

ОТКРЫТЫЙ ИНТЕГРИРОВАННЫЙ УРОК ПО ТЕМЕ

«ПОСТРОЕНИЕ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ. РЕШЕНИЕ ЗАДАЧ ПОВЫШЕННОЙ ТРУДНОСТИ» В 9 КЛАССЕ.

Учитель: Галкина Валентина Ивановна.

ГБОУ СОШ №753, г.Москва

Приступая к изучению курса геометрии, я обязательно рассказываю ученикам, зачем изучается геометрия в школе, показываю, что это очень интересный раздел математики, в котором рассматриваются красивые объекты, факты, яркие приложения, что он имеет богатую историю, связанную с именами великих учёных. При этом подчёркиваю, что геометрия как теоретическая наука, возникла в Древней Греции, что многие современные геометрические термины имеют древнее происхождение. Труды древнегреческих математиков сыграли важную роль в развитии науки вообще и в геометрии в частности. Они стали достоянием общей культуры человечества. Именно поэтому, на мой взгляд, сведения об основных результатах и достижениях этого исторического периода непременно должны входить в обязательный минимум содержания образования выпускника средней школы.

Как нельзя лучше об этом можно поговорить при изучении темы « Правильные многоугольники».

Изучение темы начинаю с определения правильных многоугольников, как выпуклых многоугольников, имеющих равные углы и равные стороны. На втором уроке рассматриваем невыпуклые правильные многоугольники, большую часть времени уделяя пентаграмме или звёздчатому пятиугольнику. В связи с этим сообщаю о пифагорейском братстве, об их опознавательном знаке и символе здоровья – пентаграмме.

Пифагорейцы дали философское объяснение устройства мира, тесно связанное с математикой. Выделяя стихии как первооснову бытия, древние учёные приписывали их атомам форму правильных

многогранников, а именно: атомам огня-форму тетраэдра, атомам земли- форму гексаэдра, атомам воздуха- форму октаэдра, атомам воды- форму икосаэдра, всей Вселенной присваивалась форма додекаэдра. Кроме правильных многогранников красивую форму имеют звёздчатые многогранники. Их всего четыре. Первые два были открыты немецким астрономом и математиком И. Кеплером, а два других построил французский инженер, механик, математик Л. Пуансо. Гранью правильного звёздчатого многогранника является пентограмма, которая обладает замечательными математическими свойствами. Она содержит все пропорции, известные пифагорейцам: арифметическую, геометрическую, гармоническую и так называемую золотую.

На третьем уроке доказываем теоремы:

1).Если окружность разделена на некоторое число равных частей (больше двух), то :

а) соединив хордами каждые две соседние точки деления, получим правильный вписанный многоугольник;

б) проведя через все точки деления касательные, продолжив каждую из них до взаимного пересечения с касательными соседних точек деления, получим правильный описанный многоугольник.

2). Если многоугольник правильный, то:

а) около него можно описать окружность;

б) в него можно вписать окружность.

В ходе третьего урока большое внимание уделяю решению задач на деление отрезка в крайнем и среднем отношении или в отношении золотого сечения. Учащиеся знакомятся с золотым прямоугольником, с золотым треугольником, с золотой спиралью.

Много внимания уделяю вопросам использования золотого сечения в живописи, скульптуре, архитектуре.

Последующие два урока отводятся на решение задач по вычислению сторон правильных многоугольников, их площадей. Обязательно рассматривается задача на доказательство о том, что сторона правильного десятиугольника равна большему отрезку радиуса, разделённого в среднем и крайнем отношении.

Завершает тему урок на решение задач повышенной сложности, конспект которого прилагается.

Конспект урока на тему : «Построение правильных многоугольников.

Решение задач повышенной сложности»

( Урок посвящается юбилею со дня рождения А.С. Пушкина )

Цель урока: научиться строить правильные десятиугольник и пятиугольник.

Задачи урока:

- закрепить знания учащихся по построению правильных многоугольников;

- преодолеть в сознании учеников представление о « сухости» предмета, оторванности от жизни и практики;

- показать красоту решения задач на построение с помощью циркуля и линейки;

- показать связь геометрии с литературой, философией,музыкой,искусством.

Ход урока.

Учитель: Здравствуйте, ребята! Сегодня у нас необычный урок математики. Мы посвящаем этот урок юбилею со дня рождения А.С.Пушкина.

Под музыку Г.Свиридова звучат отрывки из стихотворений великого поэта А.С.Пушкина « Я помню чудное мгновенье», «Бахчисарайский фонтан», «Зимнее утро». По окончании чтения стихов пара девятиклассников исполняют вальс.

Учитель: Конечно вы все узнали автора прозвучавших строк. Да. Именно А.С. Пушкин. Пушкин – великий поэт, имя которого известно всему миру, юбилей которого отмечается в июне этого года. Прислушайтесь к себе, к своему душевному состоянию. Вам понравилось? А кто почувствовал радость в душе от созвучия музыки и человеческих движений? Можете объяснить?

Когда созвучны - -это значит гармоничны, это значит красивы.

Учитель: Я предлагаю вашему вниманию строки из воспоминаний И.Кеплера и прошу подумать над тем, по какому случаю звучит восторг в его словах?

«Восемь месяцев назад предо мной блеснул первый луч света, за три месяца увидел я день и наконец, совсем недавно я смог увидеть лучезарное солнце… Я похитил золотые сосуды египтян, чтобы создать из них храм моему божеству вдали от пределов Египта… Жребий брошен. Я пишу свою книгу. Прочтётся ли она моими современниками или потомством - мне всё равно – она найдёт своего читателя. Разве Господь Бог не ждал шесть тысяч лет созерцателя своего творенья?»

Вместе с учащимися выясняем, что зрелище, представшее перед ним – Вселенная, хранящая множество тайн. И одна из них в результате титанического труда Кеплера вдруг открылась ему. Теперь она известна всему культурному миру как третий Закон Кеплера: КВАДРАТ ОТНОШЕНИЯ ПЕРИОДОВ ДВУХ ПЛАНЕТ РАВЕН КУБУ ОТНОШЕНИЯ ДЛИН БОЛЬШИХ ПОЛУОСЕЙ ИХ ОРБИТ.

Учитель: Можно спросить: «А что ему орбиты, чтобы так ликовать?». Ответ находим у другого мыслителя, Эйнштейна.

«Ощущение тайны – наиболее прекрасное из доступных нам переживаний. Именно это чувство стоит у колыбели истинного искусства и настоящей науки».

Учитель: Как видим восторгаться можно открытиями, стихами, танцами, музыкой… А можно ли испытывать эти чувства восторга, красоты, восхищения при изучении математики?... Безусловно. Именно красивым, более совершенным всегда считалось решение задач на построение, если оно содержит как можно меньше этапов построения. Вообще, задачи на построение чрезвычайно содержательны в математическом и логическом отношении. Это настоящие математические исследования в миниатюре. Начнём с самой окружности, являющейся основным элементом при решении задач на построение. Окружность самая простая из всех кривых линий, в тоже время самая древняя и таинственная геометрическая фигура. Древние философы придавали окружности огромное значение. По Аристотелю, вся небесная материя, т.е. звёзды, планеты, могут вращаться только по окружности, как по самой совершенной линии. Эта теория просуществовала несколько столетий. Окружность является симво-лом многих явлений, предметов, состояний.

Ну и естественно, деление окружности на равные части для построения правильных многоугольников имело важное значение для пифагорейцев, которые утверждали, что число лежит в основе всех явлений мира.

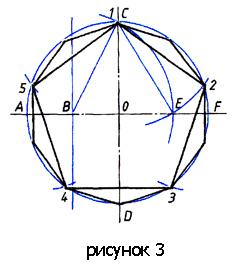
Учитель: Вспомним, какие правильные многоугольники мы уже научились строить.

Учащиеся: Правильный треугольник, правильный четырёхугольник, правильный шестиугольник и т.д. (Ученики строят фигуры с помощью циркуля и линейки).

Учитель: На сегодняшнем уроке мы рассмотрим задачи повышенной трудности.

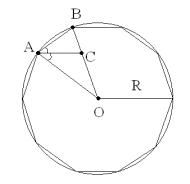
№1210 («Геометрия,7-9», Л.С.Атанасян).

Впишите в окружность правильный десятиугольник.

Учащийся : При решении этой задачи я предлагаю воспользоваться свойством стороны правильного десятиугольника, а именно, сторона правильного десятиугольника равна большей части радиуса, разделённого в отношении золотого сечения. (Учащиеся строят правильный десятиугольник).

Далее ученик коротко сообщает о том, что термин «золотое сечение» ввёл известный художник Леонардо да Винчи. Он назвал золотым сечением деление отрезка таким образом, что отношение всего отрезка к большей части равно отношению его большей части к его меньшей части. В эпоху Возрождения золотое сечение было очень популярно среди художников, архитекторов, скульпторов. В большинстве живописных пейзажей линия горизонта делит полотно по высоте в отношении золотого сечения. А выбирая размеры самой картины старались, чтобы отношение ширины к высоте тоже равнялось отношению золотого сечения. Такой прямоугольник стали называть «золотым». Бывает и «золотой треугольник». Это равнобедренный треугольник, у которого в отношении золотого сечения находятся длина боковой стороны и основания треугольника. «Золотой» треугольник использовал Леонардо да Винчи в композиции картины «Джоконда». А вот что сказал о золотом сечении И.Кеплер:

«Геометрия владеет двумя сокровищами: 1) теорема Пифагора; 2)деление отрезка в крайнем и среднем отношении. Первое можно сравнить с мерой золота, второе же больше напоминает драгоценный камень».

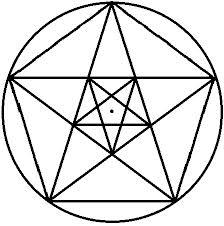
Учащийся: Пятиконечная звезда – пентаграмма всегда привлекала внимание людей совершенством формы. Пифагорейцы именно её выбрали символом своего союза. Она же считалась амулетом здоровья. Пентаграмму никто не изобретал, её только копировали с натуры. Вид пятиконечной звезды имеют пятилепестковые цветы плодоносных деревьев и кустарников, морские звёзды. Те и другие создания природы человек наблюдает уже тысячи лет. Знак пятиконечной звезды уходит своими корнями в Месопотамию. Он был впервые обнаружен при раскопках древнего Вавилона. Это был геометрический знак пяти планет (Юпитера,Сатурна,Меркурия, Марса,Венеры). Знак пентаграммы всегда употреблялся в виде защитного орудия против нападения злых, враждебных сил и являлся средством покорения их.

Учащийся: Используя пентаграмму, можно расшифровать информацию ноты «ДО». Нота связана с основой жизненного начала в материальном мире. Слово «ДО» указывает на то , что мы, будучи творцами , должны сами потроить дом в мироздании, где буква «Д» символизирует дом, а буква «О» - мир, мироздание.

Учитель: Но только ли пентаграмма , эта удивительная геометрическая фигура, даёт нам толкование какой-либо информации? Оказывается, нет. Обратите внимание на эту фигуру.

Она нам мало что говорит, а нашему гению поэту А.С.Пушкину она дала возможность высказать гипотезу о происхождении арабских цифр.

«Форма арабских цифр составлена из следующей фигуры»-такую запись мы находим в одном из томов А.С.Пушкина его полного собрания сочинений.

1 2 3 4 5

Ↄ

6 7 8 9

К сожалению, Александр Сергеевич не объяснил специализацию цифр, т.е принцип начертания. Схема А.С. Пушкина предусматривает, что скелеты фигур составлены только из треугольников и отрезков, соединяющих точки, лежащие на сторонах или диагоналях квадрата. Эта схема удовлетворяет и принципу числа углов, которые образуют иероглифы цифр,если будем читать только прямые или острые ( внешние и внутренние) углы. Так иероглиф, изображающий цифру «1», образует один угол, «2»-два угла и т.д. Это, несомненно,остроумная и удачная догадка. Изящно решается задача о нуле как о такой цифре, которая символизирует какого бы то ни было значащего числа: для этого применена фигура, не имеющая никаких углов, т.е. окружность. Таким образом, схема А.С.Пушкина является логически стройной. И если даже эта гипотеза никакого исторического основания не имеет, то она даёт возможность увидеть эволюцию взглядов на историю математики.

Учитель: Геометрические фигуры дают возможность для создания новых систем, теорий. Одной из них является психогеометрия – уникальная практическая система анализа личности. Психогеометрия позволяет :1) мгновенно определить форму или тип личноти интересующего вас человека; 2) дать подробную характеристику личных качеств и особенностей поведения человека. Эта система сложилась в США, точность диагностики – 85%. Посмотрите на эти фигуры:

Выбирайте из них ту, в отношении которой вы можете сказать – это «Я». Постарайтесь почувствовать свою форму. Если испытываете затруднение, тогда выбирайте ту, которая первой привлекла вас (см.приложение).

Рефлексия:Прдолжите предложение. Сегодня я на уроке узнал… я закрепил…я научился… Оцените свою деятельность на уроке по десятибальной шкале. Поставьте точку на шкале.

!------!------!------!------!-------!-------!------!------!------!-------!

0 1 2 3 4 5 6 7 8 9 10

Итог урока.

Приложение.

Если вы выбрали квадрат, то:

Вы -неутомимый труженик! Трудолюбие, усердие, потребность доводить начатое дело до конца, упорство, позволяющее добиваться завершения работы – вот чем знамениты истинные «квадраты». Все сведения у «квадратов» систематизированы, разложены по полочкам. «Квадрат» способен выдать необходимую информацию моментально. Поэтому «квадраты» заслуженно слывут эрудитами, по крайней мере, в своей области. «Квадраты» любят раз и навсегда заведённый порядок. Это способствует тому, что «квадраты» становятся отличными администраторами, исполнителями, но…увы редко бывают хорошими распорядителями, менеджерами. Кроме того, рациональность, сухость, холодность мешают им быстро устанавливать контакт с людьми.

Если вы выбрали треугольник, то:

Вы – лидер. Характерная особенность «треугольников» - способность концентрироваться на главной цели. Они энергичные, неудержимые, сильные личности, которые ставят ясные цели и достигают их. «Треугольники» сосредотачиваются на главном, на сути проблемы. «Треугольник» - это очень уверенный человек, который хочет быть правым во всём. Они честолюбивы, стремятся сделать карьеру. Из них получаются хорошие менеджеры. «Треугольники» на пути к вершинам власти могут идти по головам других. Они заставляют всех вращаться вокруг себя, без них жизнь потеряла бы свою остроту.

Если вы выбрали прямоугольник, то:

Вы – человек, который не удовлетворён тем образом жизни, который ведёт сейчас. «Прямоугольники» заняты постоянным поиском лучшего положения. Характерные черты – непоследовательность и непредсказуемость поступков. «Прямоугольники» имеют низкую самооценку, стремятся стать лучше, ищут новые методы работы, стили жизни. Эти люди любознательны, пытливы, и …смелы.

Если вы выбрали круг, то:

Вы - человек, который искренне заинтересован в хороших межличностных отношениях. «Круг»- самый доброжелательный из всех. Они лучшие слушатели. Обладают высокой чувствительностью, способностью сопереживать, сочувствовать, к ним тянутся люди. «Круги» слабые менеджеры и руководители в сфере бизнеса. Они не отличаются решительностью. Зато «круг» - прирождённый психолог.