Получите свидетельство
Вход
Конспект интегрированного урока русского языка и алгебры в 9 классе
Тема: Решение квадратных уравнений. Виды придаточных предложений.
Цель урока: обобщить и систематизировать знания учащихся о способах решения квадратных уравнений, формировать навыки рения квадратных уравнений, научить учащихся различать виды придаточных предложений.
Планируемые результаты урока:
Предметные.
- русский язык: формирование лингвистических знаний о видах придаточных предложений и особенностях их использования в речи;
- математика: повторение и обобщение знаний о способах решении я квадратных уравнений.
Метапредметные.
Познавательные УУД.
Делать выводы на основе полученной информации. Осуществлять подбор аргументов
для обоснования ответа. Умение строить речевые высказывания в устной и
письменной формах. Умение работать с текстом.
Коммуникативные УУД.
Умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи.
Познавательный интерес к математике и русскому языку. Осознание важности
изучения математики (логики) для понимания окружающего мира. Понимать смысл
поставленной задачи, выстраивать аргументацию, приводить примеры.
Умение воспринимать информацию на слух, выражать свои мысли. Умение
организовывать свою работу согласно инструкциям учителя. Умение строить
эффективное взаимодействие с одноклассниками при выполнении совместной работы.
Личностные УУД.
Умение соблюдать дисциплину на уроке. Умение применять полученные знания в
практической деятельности. Потребность в справедливом оценивании своей работы и
работы одноклассников.
Регулятивные УУД.
Умение определять цель работы, оценивать полученные результат. Развитие навыков
самооценки и самоанализа.
Ход урока
Организационный момент. Приветствие, целеполагание.
Учитель русского языка: Здравствуйте, ребята! Сегодня мы проведём для вас необычный урок. Но прежде чем начать нашу работу, мы предлагаем вам ответить на вопрос; «Можно ли одновременно хорошо знать и русский язык, и математику»?
Обсуждение с детьми
Учитель русского языка: Ребята, из истории мы знаем таких людей, которые одинаково владели и филологией, и математикой. Обратите внимание на экран (демонстрирует фотографии известных людей – математиков и филологов)
Актуализация знаний. Проверка домашнего задания.
Учитель математики: Ребята, дома вы повторяли материал о том, как решить квадратное уравнение. Заполните пропуски и определите вид придаточных предложений.
Квадратное уравнение – это уравнение вида _ах2 +вх +с_, в котором x – переменная, a, b и c –некоторые числа, причем а отлично от нуля (сложноподчинённое предложение с придаточным определительным).
Чтобы определить количество корней квадратного уравнения, необходимо найти ДИСКРИМИНАНТ, который вычисляется по формуле D = b2 – 4 ac (сложноподчинённое предложение с придаточным цели и придаточным определительным)
Е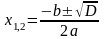
сли D 0 , то уравнение имеет два корня, которые можно найти по формуле
Е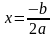
сли D = 0 , то уравнение имеет один корень , который можно найти по формуле
Если D
Групповая работа
Каждая группа получает карточки с комбинированным заданием – решить квадратное уравнение и записать ход решения, используя заранее заданные схемы сложносочинённых предложений с определённым видом придаточного. У каждой группы – свой вид придаточного предложения. В результате работы другие группы должны определить, каким видом предложения какая группа пользовалась.
В работе учащиеся используют таблицу «Виды придаточных предложений», которая заполнена ими на протяжении предыдущих уроков, каждый из которых был посвящён изучению отдельного вида придаточных предложений.
Задания для групп:
| Задание для группы № 1
Решите в тетради квадратные уравнения. Запишите результат определения количества корней по дискриминанту, используя придаточное условия. Составьте схему предложения.
12х2 + 7х + 1 = 0 9х2 + 6х + 1 = 0 3х2 – 4х + 3 = 0
Работайте по алгоритму: D = Если D …, то уравнение имеет … Схема предложения Решение уравнения
|
| Задание для группы № 2
Решите в тетради квадратные уравнения. Запишите результат определения количества корней по дискриминанту, используя придаточное следствия. Составьте схему предложения.
12х2 + 7х + 1 = 0 9х2 + 6х + 1 = 0 3х2 – 4х + 3 = 0
Работайте по алгоритму:: D = D …, (поэтому, так что) уравнение имеет … Схема предложения Решение уравнения
|
| Задание для группы № 3
Решите в тетради квадратные уравнения. Запишите результат определения количества корней по дискриминанту, используя придаточное причины. Составьте схему предложения.
12х2 + 7х + 1 = 0 9х2 + 6х + 1 = 0 3х2 – 4х + 3 = 0
Работайте по алгоритму: D = Уравнение имеет… , (потому что, так как) D … Схема предложения Решение уравнения
|
Работа по группам
Выступление групп
Группы выходят к доске, после оформления решения группы определяют, какой вид придаточного использовала выступавшая группа.
Рефлексия
- Какое уравнение называется квадратным?
- Как решить квадратное уравнение?
- Перечислите известные вам виды придаточных предложений.
Домашнее задание
0 , то уравнение имеет два корня, которые можно найти по формуле Если D = 0 , то уравнение имеет один корень , который можно найти по формуле Если D Сложноподчинённые предложения с придаточными условия и придаточными определительными" width="640"
0 , то уравнение имеет два корня" width="640"
Интегрированный урок "Решение квадратных уравнений" (995.34 KB)
0
265
4
Нравится
0
