Интегралы. Методы их решения.

КУРС АЛГЕБРЫ

ИНТЕГРАЛЫ

Пособие предназначено для студентов Академических Лицеев по направлению точные науки.

Авторская публикация включает в себя следующие разделы:

Функции нескольких переменных. Область определения. Предел функции.

Непрерывность. Частные производные. Полный дифференциал, его связь с частными производными. Инвариантность формы полного дифференциала.

Касательная плоскость и нормаль к поверхности. Геометрический смысл полного дифференциала. Частные производные и полные дифференциалы высших порядков. Формула Тейлора. Неявные функции. Теорема существования. Дифференцирование неявных функций. Экстремумы функций нескольких переменных. Необходимое условие экстремума.

Функции нескольких переменных. Область определения. Предел функции. Непрерывность. Частные производные. Полный дифференциал, его связь с частными производными. Инвариантность формы полного дифференциала. Касательная плоскость и нормаль к поверхности. Геометрический смысл полного дифференциала. Частные производные и полные дифференциалы высших порядков. Формула Тейлора. Неявные функции. Теорема существования. Дифференцирование неявных функций. Экстремумы функций нескольких переменных. Необходимое условие экстремума.

Первообразная. Неопределенный интеграл и его свойства. Методы интегрирования. Замена переменной, интегрирование по частям в неопределенном интеграле. Интегрирование рациональных дробей

Интегрирование иррациональных выражений. Интегрирование тригонометрических выражений. Задачи, приводящие к понятию определенного интеграла. Определенный интеграл , его свойства. Формула Ньютона-Лейбница, ее применение для вычисления определенных интегралов. Интегрирование по частям. Замена переменной в определенном интеграле. Геометрические и механические приложения определенного интеграла. Несобственные интегралы с бесконечными пределами и от неограниченных функций, их основные свойства. Геометрические приложения несобственных интегралов

В данном курсе рассматриваются различные подходы к определению понятия интегралов и методов их нахождения а так же действий над ними.

Предлагаемый сборник содержит примеры и их решения по вышеуказанным разделам.

Примеры решения некоторых типовых задач

Неопределенный интеграл

Пример 1. Найти .

Решение.

.

Пример 2. Найти .

Решение.

.

Пример 3. Найти .

Решение.

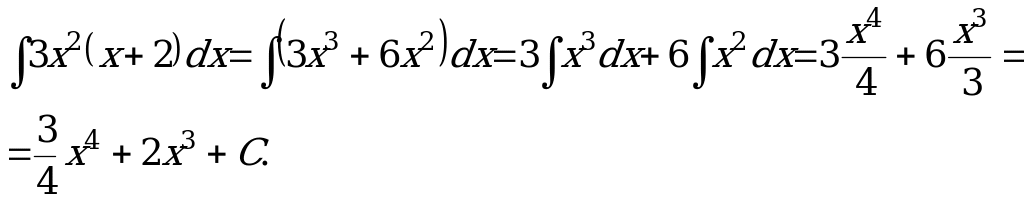
Пример 4. Найти .

Решение. Преобразуя подынтегральное выражение так, чтобы можно было воспользоваться формулой 10, имеем

Здесь .

Пример 5. Найти .

Решение. Данный пример демонстрирует довольно часто используемый прием деления числителя на знаменатель.

Пример 6. Найти .

Решение. Привести интеграл к табличному дает возможность введения новой переменной интегрирования. Используя равенство , получаем

.

Пример 7. Найти .

Решение. Введем новую переменную интегрирования, используя равенство , тогда

.

Пример 8. Найти .

Решение. Заметим, что , следовательно,

Пример 9. Найти .

Решение. С целью введения новой переменной воспользуемся равенством , тогда

Пример 10. Найти .

Решение. Учитывая, что , преобразуем подынтегральное выражение к нужному виду и находим интеграл:

Пример 11. Найти .

Решение. Данный интеграл не является табличным, для его нахождения воспользуемся заменой переменной:

Иногда замена переменной производится следующим образом. Пусть требуется найти интеграл , сделаем замену, принимая , где - непрерывная функция с непрерывной производной, тогда и интеграл принимает вид

.

После интегрирования переменную нужно заменить через х, исходя из равенства .

Пример 12. Найти .

Решение. Чтобы избавиться от иррациональности, следует сделать замену , тогда , при этом получаем

Интегрирование по частям

Формула интегрирования по частям имеет вид:

,

где - дифференцируемые функции.

Для применения этой формулы подынтегральное выражение следует представить в виде произведения функции u на дифференциал другой функции – dv, при этом целесообразно в качестве u выбирать функцию, упрощающуюся при дифференцировании ( и т.д.). Если же подынтегральное выражение есть произведение целой рациональной функции на тригонометрическую функцию или показательную функцию, то за u следует принимать целую рациональную функцию. Применение формулы интегрирования по частям целесообразно в тех случаях, когда интеграл будет проще исходного интеграла или когда он будет ему подобен.

Пример 13. Найти .

Решение. Пусть , тогда

.

Применяя формулу интегрирования по частям, имеем

Замечание. При нахождении функции v по ее дифференциалу dv мы можем брать любую произвольную постоянную. Удобно считать эту постоянную равной нулю.

Пример 14. Найти .

Решение. Применим формулу интегрирования по частям, тогда

Здесь формула интегрирования по частям была применена дважды.

Иногда интегрирование по частям приводит к уравнению относительно искомого интеграла.

Пример 15. Найти .

Решение. При нахождении данного интеграла вновь используем

формулу интегрирования по частям.

Рассмотрим равенство:

.

Перенося в левую часть и разделив на 2, окончательно получим

Следует заметить, что далеко не всякая элементарная функция имеет интеграл, выражающийся в элементарных функциях. Поэтому далее рассмотрим классы функций, интегралы от которых выражаются через элементарные функции. Центральное место занимает класс рациональных функций, так как к интегрированию рациональных функций сводится интегрирование многих иррациональных и тригонометрических функций

Интегрирование рациональных функций

Рациональной функцией или рациональной дробью называется дробь вида

,

где - многочлены с действительными коэффициентами.

Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, в противном случае дробь называется неправильной.

Если дробь неправильная, то, разделив числитель на знаменатель по правилу деления многочленов, можно представить данную дробь в виде суммы многочлена и некоторой правильной дроби, т.е.

,

где - многочлен, а - правильная рациональная дробь.

Рассмотрим простейшие рациональные дроби:

1. ;

2. , где m – целое положительное число, большее единицы;

3. , квадратный трехчлен в знаменателе не имеет действительных корней, т.е. ;

4. , где п – целое положительное число

большее единицы, а квадратный трехчлен не имеет действительных корней.

Интегрирование простейших дробей первых двух типов

1.

2.

Интегрирование простейших дробей третьего типа

Пусть дан интеграл этого типа

.

В знаменателе подынтегральной функции выделяем полный квадрат

а затем подстановкой приведем интеграл к виду

,

легко сводящемуся к табличным интегралам. Поясним выше изложенный прием на примере.

Пример 1. Найти .

Решение. В знаменателе подынтегральной функции , следовательно, имеем простейшую дробь третьего типа. Так как

,

(использовали часто применяющийся прием «выделения полного квадрата»), то

.

Пусть ,

тогда

где

Интегрирование простейших дробей четвертого типа

В интеграле этого типа в знаменателе выделяют полный квадрат.

Подстановкой приводят интеграл к виду

.

Первый интеграл правой части легко приводится к табличному интегралу, а второй находится с помощью рекуррентной формулы.

Пусть , тогда

.

С помощью рекуррентной формулы интеграл сводится к интегралу , затем к ,

Известно (основная теорема алгебры), что всякую правильную рациональную дробь можно разложить на сумму простейших дробей, причем единственным образом, для этого требуется знаменатель разложить на простые множители, т. е. представить его в виде произведения многочленов первой степени или квадратных трехчленов, не имеющих действительных корней. Решая уравнение , получаем ,

где множители первой степени соответствуют действительным корням, а множители второй степени – парам мнимых сопряженных корней. После этого правильная рациональная дробь разлагается на простейшие по формуле

где - неопределенные (неизвестные) коэффициенты, некоторые из них могут равняться нулю.

Каждому множителю в разложении знаменателя соответствует столько простейших слагаемых дробей, какова его кратность .

Для нахождения неопределенных коэффициентов все простейшие дроби приводят к общему знаменателю и приравнивают числители обеих частей полученного равенства. Затем сравнивают коэффициенты при одинаковых степенях х, что приводит к системе уравнений, решая которую находят значения неизвестных коэффициентов.

Рассмотрим примеры, решения которых проиллюстрируют все

выше сказанное.

Пример 2. Разложить данные дроби на сумму простейших дробей:

а) ; б) ; в) ; г) .

Решение.

а) Корни знаменателя действительные, различные: Каждому корню в разложении соответствует одна дробь, поэтому разложение имеет вид:

.

б) Корни знаменателя - ,первый корень кратности 3, поэтому в разложении ему соответствует сумма трех дробей:

.

в) Корень знаменателя - , имеет кратность 2, квадратный трехчлен - не имеет действительных корней и не может быть разложен на множители, значит

.

г) Разложим знаменатель на множители, тогда

.

Пример 3. .

Решение. Имеем правильную рациональную дробь. Разложим знаменатель дроби на множители: .

Подынтегральную дробь представим в виде суммы простейших, т.е.

.

Чтобы найти неизвестные коэффициенты A, B, C, приведем дроби справа к общему знаменателю, тогда

.

Дроби равны, у них равны знаменатели, значит, числители тоже равны, т.е.

.

Так как многочлены слева и справа тождественно равны, то их значения равны при любых значениях х.

Придавая х значения, равные корням знаменателя данной дроби,

получим уравнения для определения коэффициентов.

При имеем .

При имеем .

Для нахождения В положим х равным любому числу, например, пусть , тогда , откуда В = 1. Следовательно,

.

Переходя к интегралу, получим

Пример 4. .

Решение. Имеем неправильную рациональную дробь. Выделим целую часть, разделив числитель на знаменатель по правилу деления многочленов:

. Здесь 2х – целая часть, 1 – остаток.

Далее, данную дробь представим в виде суммы целой части и правильной рациональной дроби, а полученную в правой части правильную рациональную дробь – в виде суммы простейших дробей, т.е.

.

В правой части последнего равенства приведем дроби к общему знаменателю и приравняем числители, после чего будем иметь

.

В данном случае действительный корень только один, поэтому способ подстановки частных значений для нахождения коэффициентов будет не удобен. Найдем коэффициенты, используя известный факт: два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях х. Раскроем скобки и приведем подобные слагаемые:

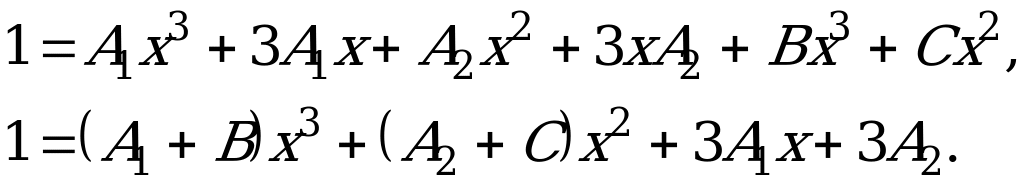
Отмечая за чертой слева, при каких х сравниваются коэффициенты, получаем систему уравнений:

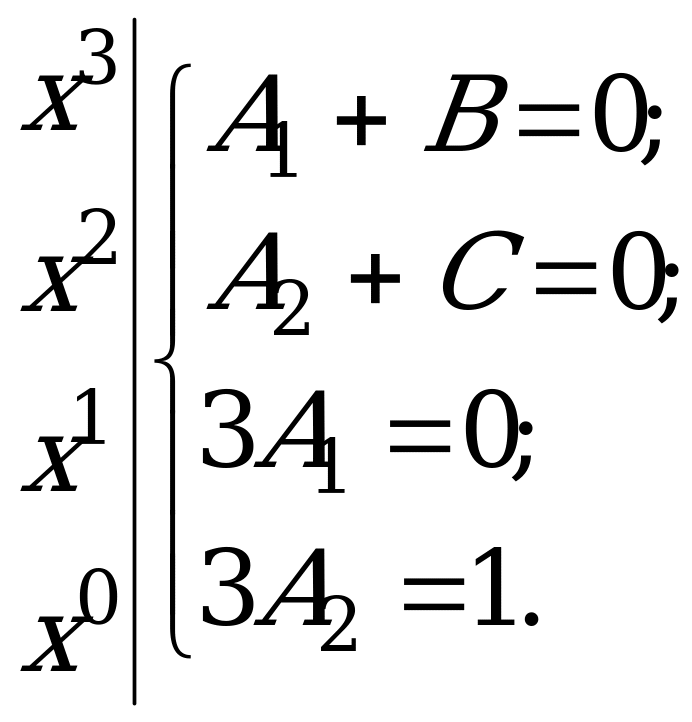
Решая систему, получаем

Окончательное разложение данной дроби на простейшие имеет вид: .

Далее, переходим к интегрированию, т.е.

Пример 5. .

Решение. В этом примере некоторую трудность представляет разложение знаменателя на множители. Полезно знать следующий искусственный прием. Подбором определяем один корень знаменателя. При х = 1многочлен обращается в 0, значит х = 1 – корень многочлена и на основании следствия из теоремы Безу этот многочлен делится без остатка на разность , т.е. знаменатель можно записать в виде:

.

Квадратный трехчлен не имеет действительных корней и на более простые множители во множестве действительных чисел не может быть разложен.

Представим подынтегральную дробь в виде суммы простейших и найдем неопределенные коэффициенты:

,

.

Заметим, что при х = 1 последнее равенство принимает вид: , найдем А, т.е. А = 1. Далее, раскрыв скобки, приводя многочлен в правой части к стандартному виду и сравнив коэффициенты при одинаковых степенях х, получим систему уравнений, решив которую получим . Подставляя найденные коэффициенты в разложение, получаем

.

Перейдем к интегрированию.

.

Второй интеграл правой части найдем отдельно, выделяя в числителе производную знаменателя, т.е.

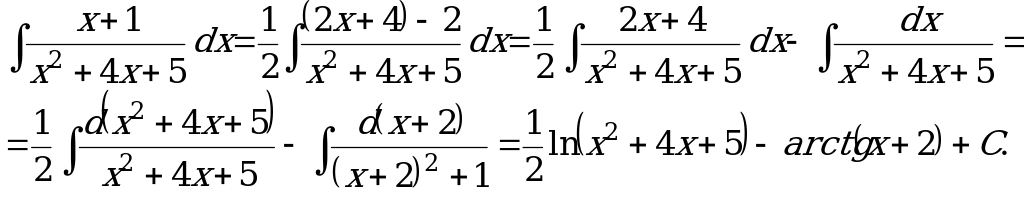Окончательно имеем

В заключении заметим, что неопределенный интеграл от любой рациональной функции выражается через элементарные функции, т.е. «берется в конечном виде».

Интегрирование тригонометрических функций

Универсальная подстановка. Рассмотрим интегралы вида

, где R – рациональная функция sinx, cosx. Интегралы такого вида подстановкой

приводятся к интегралам от рациональной дроби нового аргумента t; при такой подстановке ;

.

Пример 1. .

Решение. Воспользуемся универсальной подстановкой.

Пусть , тогда

Универсальная подстановка, хотя и дает возможность проинтегрировать всякую функцию вида , но часто приводит к сложным рациональным дробям, поэтому на практике ей пользуются лишь в крайних случаях, чаще используют следующие частные подстановки:

1) если функция нечетна относительно синуса, т.е. , то применима подстановка

;

2) если функция нечетна относительно косинуса, т.е. , то применима подстановка

;

3) если функция четна относительно синуса и косинуса, т.е. , то применима подстановка

или .

Пример 2. .

Решение. Здесь подынтегральная функция нечетная относительно

косинуса, поэтому применим подстановку .

При этом и

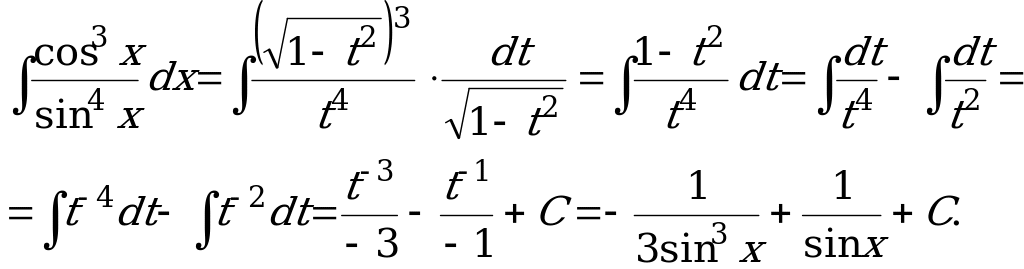
Замечание. При интегрировании тригонометрических функций иногда можно добиться результата, не применяя метод подстановки, а используя только тождественные преобразования подынтегрального выражения.

Рассмотрим решение предыдущего примера другим способом.

и т.д.

Пример 3. .

Решение.

Пример 4. .

Решение. Применим подстановку , так как подынтегральная функция является четной относительно синуса и косинуса (синус и косинус имеют четные показатели степеней).

Наряду с указанными подстановками полезно знать также другие приемы интегрирования тригонометрических функций.

Интегрирование функций вида ,

где оба показателя т и п – четные неотрицательные числа (в частности, один из них может быть равным нулю). Для вычисления интеграла следует применить формулы понижения степени, т.е.

.

Пример 5. .

Решение. Воспользуемся формулой понижения степени, тогда

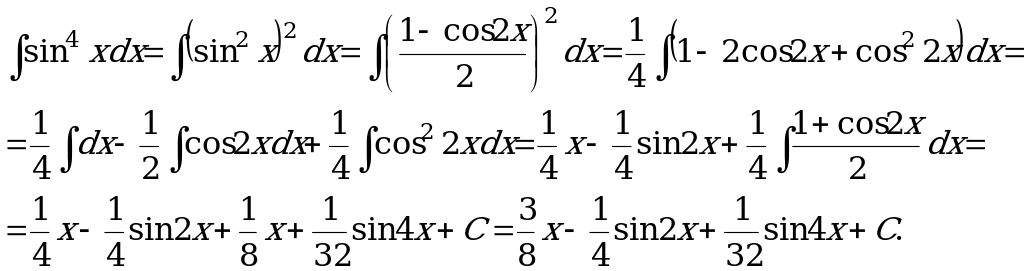Аналогичным образом можно найти интегралы , и другие.

Интегрирование функций вида

где т и п - целые положительные числа, находятся с помощью следующих тригонометрических формул:

;

;

.

Пример 6. .

Решение. Преобразуя произведение синуса на косинус в произведение, имеем , отсюда

Интегрирование иррациональных функций

Интегралы вида ,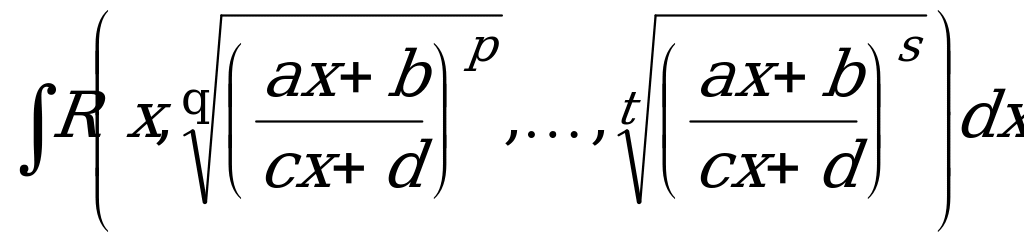

где R - рациональная функция, p, q, s, t - целые числа, приводятся к интегралу от рациональной функции с помощью подстановки

,

где п – наименьшее общее кратное показателей корней, т.е. чисел .

Интегралы вида ,

где R - рациональная функция, p, q, s, t - целые числа, приводятся к интегралу от рациональной функции с помощью подстановки

,

где п – наименьшее общее кратное показателей корней, т.е. чисел .

Пример 1. .

Решение. Наименьшее общее кратное чисел 2 и 3 равно 6, значит п = 6 и применима подстановка .

=

.

Пример 2. .

Решение. Сделаем подстановку , тогда ,

.

Выделяя в подынтегральной функции целую часть, приведем интеграл к виду:

Интегралы от некоторых иррациональных функций с помощью выделения полного квадрата в подкоренном выражении можно привести сразу к табличным интегралам. Покажем этот прием на следующих примерах.

Пример 3. .

Решение. Выделим в подынтегральном выражении полный квадрат, тогда

Пример 4. .

Решение. Здесь выделение полного квадрата приведет к использованию другой табличной формулы.

Некоторые интегралы с помощью соответствующих подстановок приводятся к интегралам от тригонометрических функций.

подстановкой или ;

подстановкой , или ; подстановкой ; или .

Такими подстановками мы избавляемся от иррациональности в подынтегральных выражениях.

Если (а 0), то

.

Если , то

.

Если , то

.

Пример 5. .

Решение. Подкоренное выражение имеет вид , поэтому в воспользуемся подстановкой .

.

Чтобы перейти к переменной х, произведем преобразования: , отсюда ,

.

Окончательно имеем

Пример 6. .

Решение.

Перейдем к старой переменной следующим образом.

Так как , значит ,

.

Итак,

Обратим внимание, этот интеграл мы уже находили методом интегрирования по частям.

Пример 7. .

Решение. Здесь воспользуемся заменой , тогда и =

=

Для того, чтобы вернуться к переменной х, воспользуемся формулой , тогда и окончательно имеем

.

Следует заметить, что рассмотренные в последних примерах интегралы иногда берутся по частям, иногда более простой заменой.

Пример 8. .

Решение. В данном случае нет смысла вводить тригонометрическую подстановку, так как интеграл легко приводится к «табличному», действительно

Интегрирование дифференциального бинома

Интегралы вида , где т, п, р – рациональные числа, называются интегралами от дифференциальных биномов. Такие интегралы берутся лишь в трех случаях с помощью специальных подстановок.

Подстановки Чебышева

1. Пусть р – целое число, тогда данный интеграл сводится к интегралу от рациональной функции с помощью подстановки

,

где s – наименьшее общее кратное знаменателей дробей т и п.

2. Пусть - целое число. В этом случае данный интеграл рационализуется с помощью подстановки

,

где s – знаменатель дроби р.

3. Пусть - целое число, тогда к рациональной функции приводит подстановка

,

где s – знаменатель дроби р.

Пример 9. .

Решение. Приведем интеграл к виду дифференциального бинома и воспользуемся одной из подстановок Чебышева (если это возможно). . Здесь – целое, наименьшее общее кратное чисел 2 и 4 равно 4, значит можно воспользоваться первой подстановкой Чебышева.

Пример 10. .

Решение. .

Здесь - целое число, применим вторую подстановку

Чебышева: .

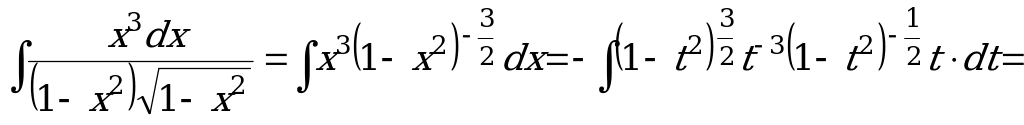
Пример 11. .

Решение. Запишем подынтегральное выражение в виде дифференциального бинома и выберем соответствующую подстановку.

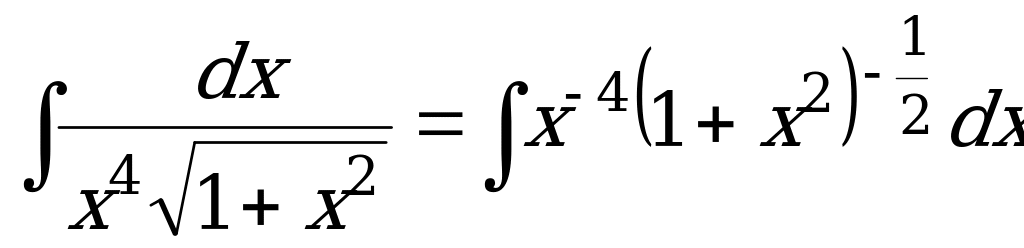. Имеем , отсюда и можем применить третью подстановку Чебышева, т.е. ,

тогда

Заметим, если не выполняется ни одно из трех перечисленных выше условий, то найти неопределенный интеграл не представляется возможным, в таких случаях говорят: «интеграл не берется в конечном виде».

Итак, необходимо знать, что имеются элементарные функции, неопределенные интегралы от которых не выражаются через элементарные функции. К таким интегралам относятся: , - «интегральный синус»; - «интегральный косинус»; - «интегральный логарифм» и другие.

Эти и другие интегралы определяют новые виды функций, которые не являются элементарными, но широко используются как в математике, так и в других областях знаний.

Определенный интеграл

Формула Ньютона-Лейбница

,

где - первообразная функция .

Формула Ньютона-Лейбница дает основной способ вычисления определенных интегралов.

Замечание. Между неопределенными и определенными интегралами существует связь, нахождение одних и вычисление других предусматривает отыскания первообразной функции, поэтому техника вычисления определенных интегралов базируется на методах нахождения неопределенных интегралов. Однако следует помнить, что неопределенный интеграл – это множество первообразных функций, а определенный интеграл – это число.

Пример 1.

Пример 2.

Пример 3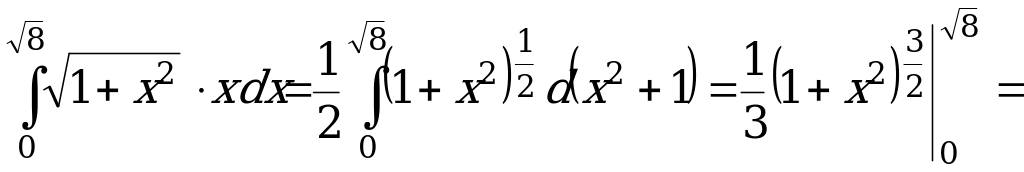

.

Методы вычисления определенных интегралов

Интегрирование по частям в определенном интеграле

Метод интегрирования по частям может быть применен к вычислению определенных интегралов, при этом используется формула

Пример 4. Вычислить .

Решение. Используем метод интегрирования по частям.

Пусть , тогда .

Замена переменной в определенном интеграле

Если на отрезке функции - непрерывны и , то

Пример 5. Вычислить .

Решение. Вычислим интеграл с помощью замены переменной.

Пусть , тогда или

Заменим пределы интегрирования:

при ; при Возвращаясь к интегралу имеем

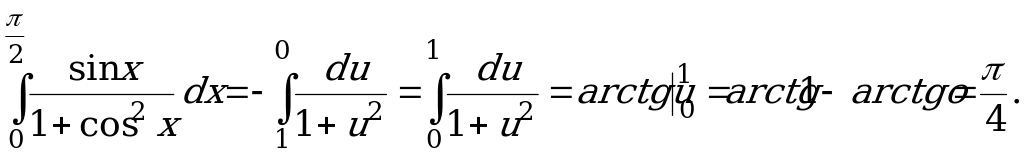
Определенный интеграл от четной или нечетной функции

по симметричному промежутку

Если - четная функция, то

,

а если - нечетная функция, то

.

Например, ,

Несобственные интегралы

Интегралы с бесконечными пределами

Если функция интегрируема на любом отрезке , где

, то для любого b существует и тем лучше

выражает величину, которую следует принять в качестве интеграла от по промежутку , чем больше , поэтому полагают

(1)

Интеграл называется сходящимся, если существует конечный предел в правой части и называется расходящимся, если указанный предел не существует или равен бесконечности.

Пусть первообразная функция подынтегральной функции известна, тогда сходимость или расходимость интеграла можно установить по формуле Ньютона-Лейбница:

.

Аналогично, если функция интегрируема на любом отрезке , где , то

(2)

Если функция интегрируема на любом отрезке , где , то,

(3)

где с – некоторое действительное число.

Интеграл называется сходящимся, если существуют и конечны оба предела в правой части равенства (3), и расходящимся,

если не существует или равен бесконечности хотя бы один из них.

Пример 1. Вычислить несобственный интеграл или доказать его расходимость.

Решение. Первообразная подынтегральной функции находится непосредственным интегрированием, поэтому

, следовательно, несобственный интеграл сходится и равен единице, т.е. .

Пример 2. Вычислить несобственный интеграл или доказать его расходимость.

Решение. Используя формулу (1), имеем

.

Следовательно, интеграл расходится.

Пример 3. Вычислить несобственный интеграл или доказать его расходимость.

Решение. По формуле (3) имеем

,

т.е. интеграл расходится.

Пример 4. Вычислить несобственный интеграл или доказать его расходимость.

Решение. Используя формулу (3), получаем

значит, интеграл сходится.

Интегралы от неограниченных функций

Если функция непрерывна на промежутке и имеет разрыв второго рода в точке , т.е. , то полагают

. (4)

Интеграл называется сходящимся, если существует конечный предел в правой чисти равенства (4), если указанный предел не существует или равен бесконечности, то интеграл называется расходящимся.

Аналогично определяется интеграл от функции , имеющей разрыв второго рода в правом конце промежутка :

. (5)

Если же функция непрерывна на промежутке , а в точке имеет разрыв второго рода, то полагают

. (6)

Интеграл называется сходящимся, если существуют и конечны оба предела в правой чисти равенства (6), и расходящимся, если не существует или равен бесконечности хотя бы один из них.

Пример 5. Вычислить несобственный интеграл или доказать его расходимость.

Решение. Функция имеет разрыв второго рода в точке , поэтому данный интеграл – несобственный, для выяснения его сходимости воспользуемся формулой (4), тогда

,

т.е. интеграл расходится.

Пример 6. Вычислить несобственный интеграл или доказать его расходимость.

Решение. Здесь подынтегральная функция имеет разрыв второго родав точке . Воспользуемся формулой (5):

,

следовательно, интеграл сходится, т. е.

.

Пример 7. Вычислить несобственный интеграл или доказать его расходимость.

Решение. Так как внутри отрезка интегрирования существует точка , где подынтегральная функция имеет разрыв второго рода, то воспользуемся формулой (6) и представим интеграл как сумму двух слагаемых: .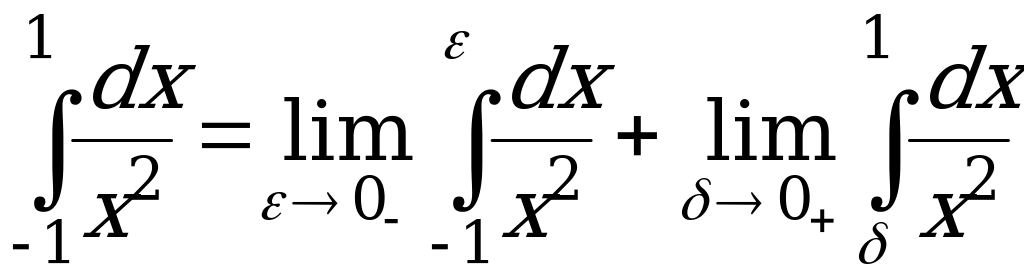

Вычислим каждый интеграл отдельно:

.

Следовательно, на промежутке интеграл расходится.

.

Значит, на промежутке интеграл также расходится.

Таким образом, данный интеграл расходящийся.

Пример 8. Вычислить несобственный интеграл или доказать его расходимость.

Решение. В данном случае подынтегральная функция имеет разрыв второго рода в обоих концах промежутка интегрирования, поэтому разобъем интеграл на два интеграла и применим формулы (4), (5).

Форма промежуточного контроля

зачет

Перечень примерных вопросов для подготовки к зачету.

ВОПРОСЫ К ЗАЧЕТУ

1.Определение функции нескольких переменных. Область определения.

2.Предел и непрерывность функции нескольких переменных.

3.Частные производные и полный дифференциал функции нескольких переменных.

4. Частные производные и полный дифференциал второго порядка.

5.Уравнеие касательной плоскости и нормали к поверхности.

6.Неявные функции. Дифференцирование неявных функций.

7.Экстремумы функции нескольких переменных.

8.Первообразная функция. Неопределенный интеграл и его свойства.

9.Таблица неопределенных интегралов.

10.Непосредственное интегрирование.

11.Интегрирование по частям и замена переменной в неопределенном интеграле

12.Интегрирование рациональных функций.

13.Интегрирование иррациональных функций.

14. Интегрирование тригонометрических функций.

15.Определенный интеграл. Свойства определенного интеграла.

16.Вычисление определенного интеграла. Формула Ньютона – Лейбница.

17.Замена переменной и интегрирование по частям в определенном интеграле.

18.Приложения определенных интегралов.

19.Несобственные интегралы с бесконечными пределами.

20. Несобственные интегралы от разрывных функций.

Основная литература

1. Шипачев В.С. Высшая математика: Учеб. для вузов / В.С. Шипачев. – 6-е изд., стер. – М.: Высш. шк., 2003. – 479 с.

2. Пискунов Н.С. Дифференциальное и интегральное исчисление: Учеб. для втузов. В 2-х т. Т. I: – М.: Интеграл – Пресс, 2004. – 416 с.

3. Шипачев В.С. Задачник по высшей математике: Учеб. пособие для вузов / В.С. Шипачев. – 3-е изд., стер. – М.: Высш. шк., 2003. – 304 с.

4. Баврин И.И. Высшая математика: Учеб. для студ. естественнонаучных специальностей педагогических вузов. – 2-е изд., стер. – М.: Изд. центр «Академия»; Высш. шк., 2001. – 616 с.

5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч. I: Учеб. пособие для втузов. – 5-е изд., испр. – М.: Высш. шк., 1999. – 304 с.

6. Письменный Д.Т. Конспект лекций по высшей математике: Полный курс. – М.: Айрис-пресс, 2004.

7. Лунгу К.Н., Письменный Д.Т. Сборник задач по высшей математике. 1 курс. – М.: Айрис-пресс, 2004.

1. Глазырин В.В., Лесков В.П., Лескова Т.М., Чистякова С.А. Высшая математика частьII (учебное пособие для заочников).