Тема: I признак равенства треугольников.
Класс: 7
Цели:
а) познакомить учащихся с определением треугольника и его элементов, формулировкой и доказательством I признака равенства треугольников; научить в равных треугольниках выделять пары равных элементов, распознавать на рисунке пары равных треугольников, применять признак равенства треугольников при решении задач;
б) развивать приемы логического мышления (сравнивать, обобщать), правильно формулировать и излагать мысли, умение анализировать факты и делать выводы; создать условия для развития познавательного интереса к математике;
в) воспитывать математическую культуру и речь.
План урока.
Орг. момент.(2 мин.)
Сообщение темы и целей урока.(3 мин.)
Актуализация опорных знаний.(7 мин.)
Объяснение нового материала.(7 мин.)
Закрепление изученного материала.(13 мин.)
Самостоятельная работа.(7 мин.)
Итог урока.(3 мин.)
Задание на дом.(2 мин.)
Рефлексия.(1 мин.)
Ход урока.
Орг. момент.
Здравствуйте, ребята. Садитесь.
Сообщение темы и целей урока.
Тема нашего урока – I признак равенства треугольников. Давайте вспомним, что такое треугольник? Какие фигуры называются равными? (Две фигуры называются равными, если их можно совместить наложением)
Актуализация опорных знаний.
Теперь мы будем доказывать теорему, но нам нужны те знания, которые мы получили в этом году в курсе геометрии:
- Сколько прямых можно провести через две точки? (1)
- Сколько общих точек могут иметь две прямые? (1 или 0)
- Какие углы называются смежными? (Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой)
- Чему равна сумма смежных углов? (180)
- Какие углы называются вертикальными? (Два угла называются вертикальными, если стороны одного угла являются продолжениями другого)
- Каким свойством обладают вертикальные углы? (Вертикальные углы равны)
Ребята, посмотрите на доску, скажите, что на ней изображено?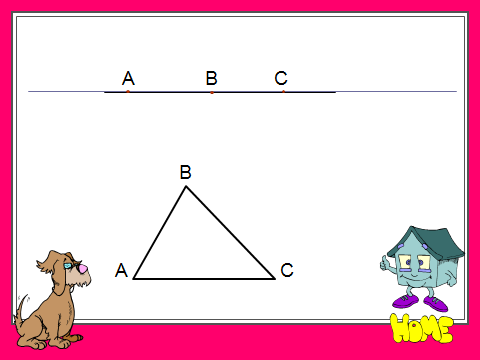
Обратите внимание на то, что три точки, являющиеся вершинами треугольника, не лежат на одной прямой. Почему точки не лежащие на одной прямой? (прямая, все точки, которой лежат на прямой)
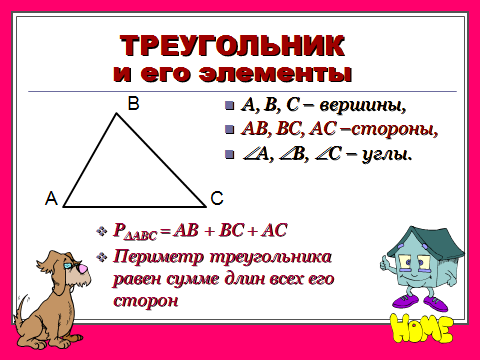
В треугольнике всего 6 элементов: 3 стороны и 3 угла.
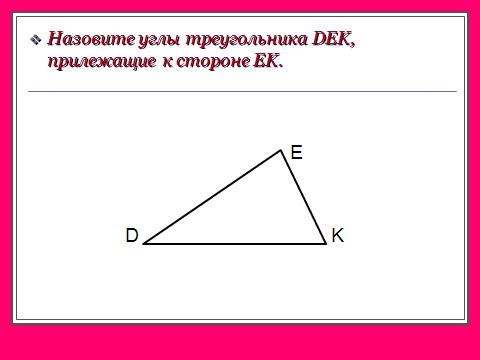
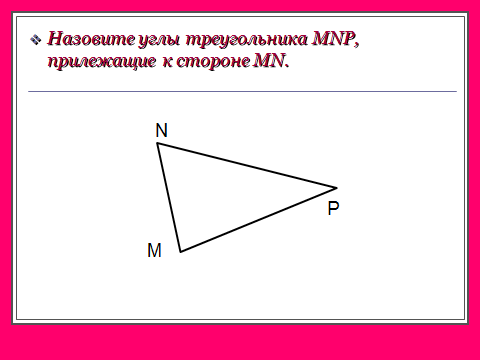
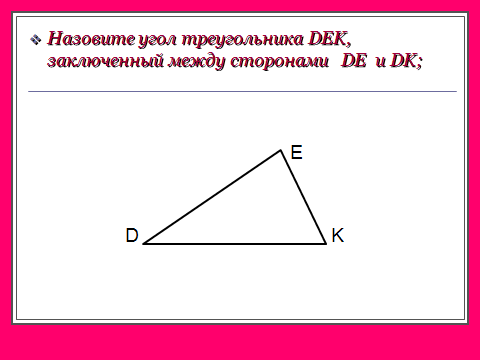
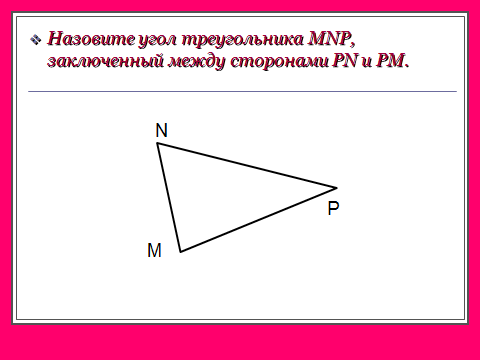
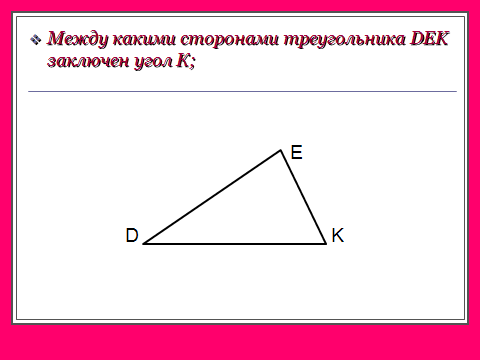
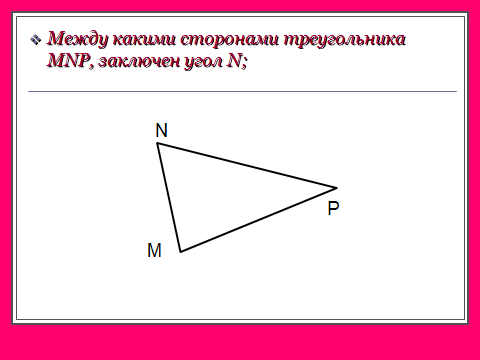
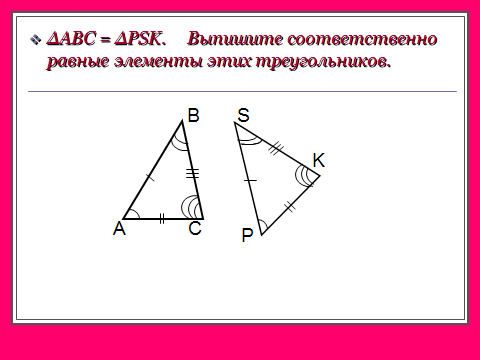
В равных треугольниках против соответственно равных сторон лежат равные углы, и наоборот: против соответственно равных углов лежат равные стороны.
(Напомнить учащимся как с помощью штрихов и дужек обозначаются равные стороны и углы)
У вас на парте лежат треугольники (Приложение 2.), среди них есть равные. Давайте их найдем. Если наложить две стороны и угол между ними … Если наложить сторону и два прилежащих к ней угла… Если наложить три стороны…Равны ли треугольники с равными углами… Сколько элементов одного треугольника нам надо соотнести с элементами другого треугольника, чтобы установить равенство треугольников? (3)
Объяснение нового материала.
А теперь непосредственно перейдем к теме нашего урока, т.к. по определению треугольники равны, если они совпадают при наложении. А если мы не можем наложить, то у нас существуют признаки равенства треугольников, один из которых мы сегодня докажем.

У вас на парте есть заготовки доказательства теоремы…( приложение 3.)
5 – 7 мин. Прежде чем приступить к решению задач, запишите домашнее задание:
Вопросы п.14, 15 №1-4, стр.49 (устно), №95, 98.
Закрепление изученного материала.
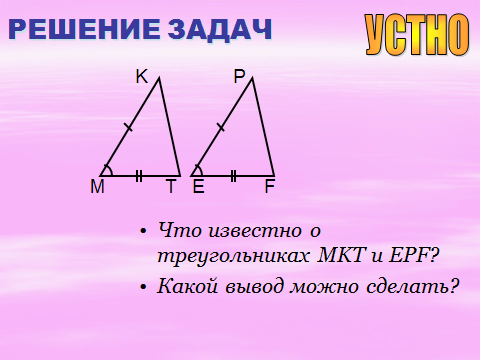
Треугольники полностью по I признаку.
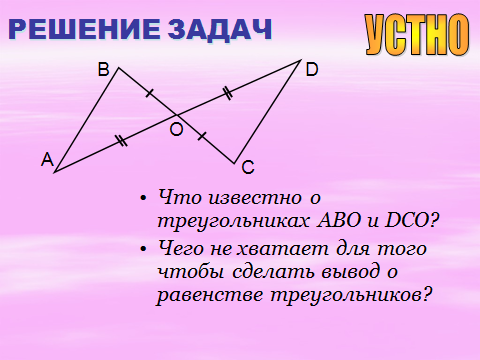
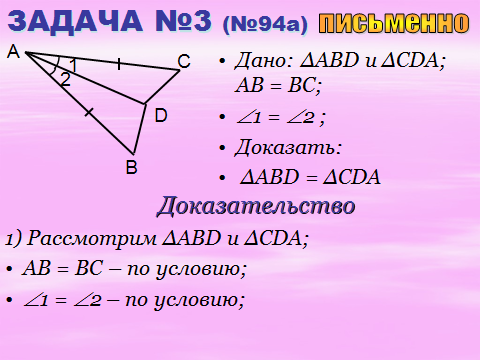
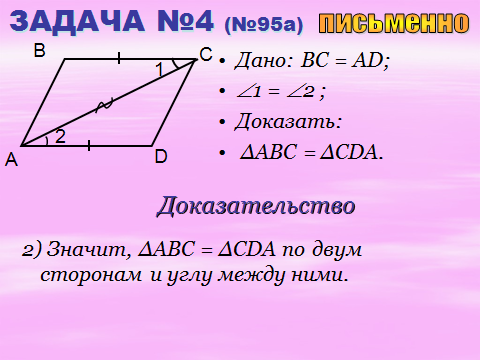
самостоятельно
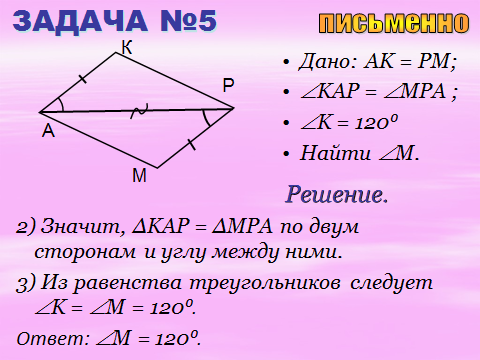
Самостоятельная работа. Приложение 1.
Итог урока.
Треугольник играет в геометрии особую роль.
Без преувеличения можно сказать, что вся (или почти вся) геометрия со времён «Начал» Евклида покоится на «трёх китах» – признаках равенства треугольников.
Мы с вами изучили 1 признак равенства треугольников.
Сформулируйте первый признак равенства треугольников, т.к. вы его запомнили за этот урок.
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Задание на дом. Вопросы п.14, 15 №1-4, стр.49 (устно), №95, 98.
Рефлексия.
Приложение 1. Самостоятельная работа.
Самостоятельная работа. Вариант I.
Закончите предложения:
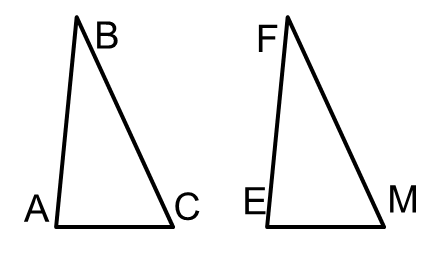
∆ABC = ∆EFM по первому признаку, если
а) AB = EF, AC = EM и ___=___
б) BC = FM, ∠B = ∠F и ___=___
в) ∠С = ∠M, ___=___, ___=___.
Самостоятельная работа. Вариант II.
Закончите предложения:
∆ABC = ∆MDK по первому признаку, если
а) AB = MD, AC = MK и ___=___
б) BC = DK, ∠B = ∠D и ___=___
в) ∠С = ∠K, ___=___, ___=___.
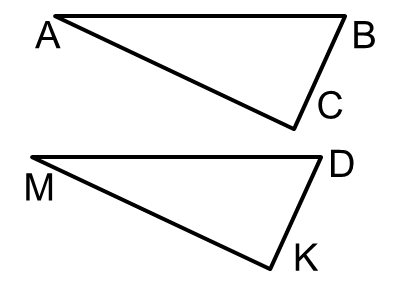
Приложение 2. Треугольники.




Приложение 3.
I признак равенства треугольников
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.



Доказательство:
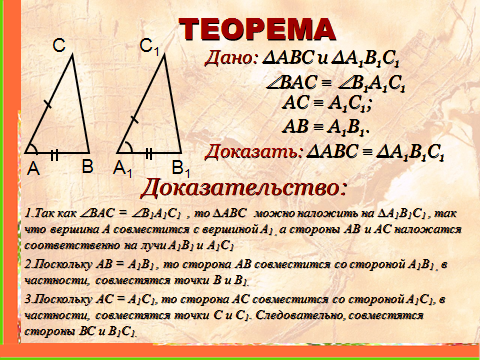
1.Так как ВAС = B1A1C1 , то ∆ABC можно наложить на ∆A1B1C1 , так что вершина А совместится с вершиной A1 , а стороны АВ и АС наложатся соответственно на лучи A1B1 и A1C1
2.Поскольку АВ = A1B1 , то сторона АВ совместится со стороной A1B1 , в частности, совместятся точки В и B1.
3.Поскольку АС = A1C1, то сторона АС совместится со стороной A1C1, в частности, совместятся точки С и C1. Следовательно, совместятся стороны ВС и В1C1.
Дано:
∆ABC и ∆A1B1C1 ВAС = B1A1C1 AC = A1C1;
AB = A1B1.
Доказать:
∆ABC = A1B1C1

 Получите свидетельство
Получите свидетельство Вход
Вход











 I признак равенства треугольников. (1.48 MB)
I признак равенства треугольников. (1.48 MB)
 0
0 214
214 6
6 Нравится
0
Нравится
0


