Графический способ решения систем уравнений

Графический способ решения систем уравнений.

Науки математические с самой глубокой древности обращали на себя особенное внимание, в настоящее время они получили еще больше интереса по влиянию своему на искусство и промышленность.

Пафнутий Львович Чебышев (1821 – 1894)

Проверка домашнего задания:

• № 405

в ) т.С (1;-4), центр окружности т.К(2;-5)

Решение:

(х - а) ² +(у - в) ² = R²

(1 - 2) ² +( -4 + 5) ² = 2

(х -2) ² + (у +5) ² = 2

Ответ: (х -2) ² + (у +5) ² = 2

Проверка домашнего задания:

• № 413 (б)

16х – 4(3х – 2) = 5

16х – 12х + 8 = 5

4х = -3

х =-3 / 4

х = -0,75

у = 3*(-0,75) - 2

у = -4,25

Ответ: (-0,75;-4,25)

Проверка домашнего задания:

• 414 (б)

*2

-х = -30

х = 30

4*30 – 2у = 170

-2у = 170 -120

-2у = 50

у = 50 /(-2)

у = -25

Ответ: (30; -25).

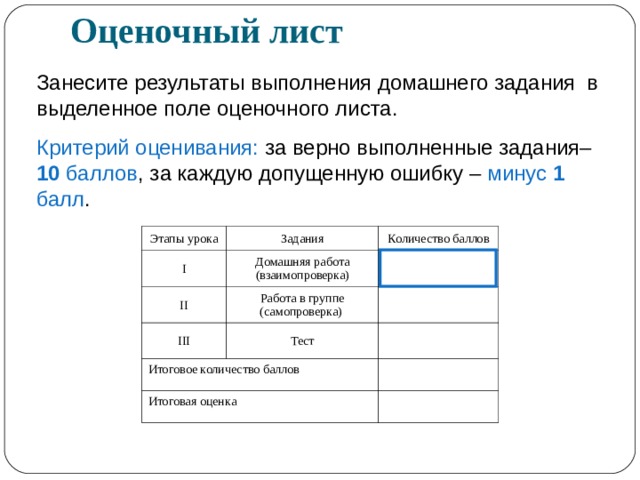
Оценочный лист

Занесите результаты выполнения домашнего задания в выделенное поле оценочного листа.

Критерий оценивания: за верно выполненные задания– 10 баллов , за каждую допущенную ошибку – минус 1 балл .

Этапы урока

I

Задания

Количество баллов

Домашняя работа (взаимопроверка)

II

III

Работа в группе (самопроверка)

Итоговое количество баллов

Тест

Итоговая оценка

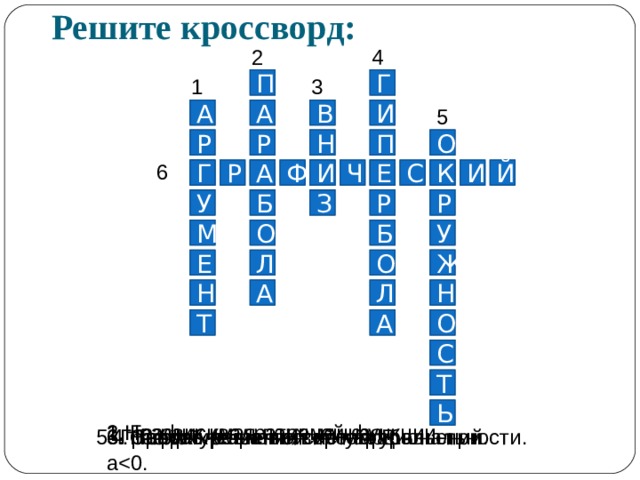
Решите кроссворд:

4

2

Г

3

1

П

А

И

В

А

5

П

Р

Н

О

Р

6

К

Г

И

И

А

Е

Е

С

А

К

Г

Р

Й

Ф

И

Ч

Р

Р

Б

З

У

У

Б

М

О

Ж

Л

О

Е

Н

Н

А

Л

О

А

Т

С

Т

Ь

1.Независимая переменная.

2. График квадратичной функции.

3. Направление ветвей параболы при а

4. График обратной пропорциональности.

5. График уравнения: х 2 +у 2 = R .

6. Способ решения систем уравнений.

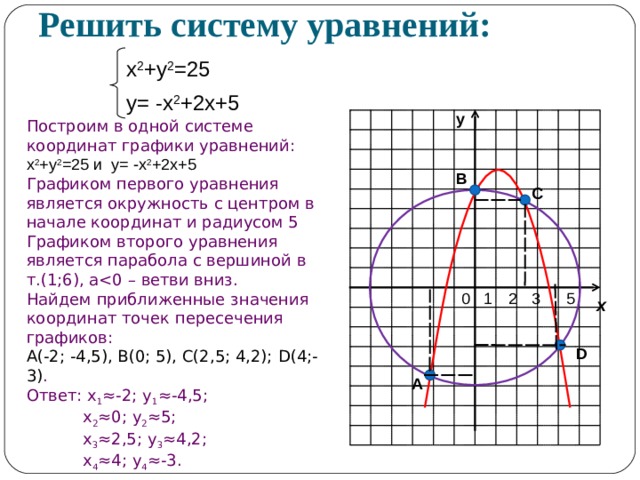
Решить систему уравнений:

х 2 +у 2 =25

у= -х 2 +2х+5

у

Построим в одной системе координат графики уравнений: х 2 +у 2 =25 и у= -х 2 +2х+5

Графиком первого уравнения является окружность с центром в начале координат и радиусом 5

Графиком второго уравнения является парабола с вершиной в т.(1;6), а

Найдем приближенные значения координат точек пересечения графиков:

А(-2; -4,5), В(0; 5), С(2,5; 4,2); D (4;-3) .

Ответ: х 1 ≈-2; у 1 ≈-4,5;

х 2 ≈0; у 2 ≈5;

х 3 ≈2,5; у 3 ≈4,2;

х 4 ≈4; у 4 ≈-3.

В

С

х

D

А

Чтобы решить систему двух уравнений с двумя неизвестными графически, нужно: 1) Построить в одной системе координат графики уравнений, входящих в систему; 2) Определить координаты всех точек пересечений графиков (если они есть); 3) Координаты этих точек и будут решениями системы.

Помните о трех вещах!

Если точек пересечения графиков нет, то система решений не имеет;

Если графики совпадают, то система имеет бесконечно много решений;

3) Координаты точек пересечения определяются приблизительно, поэтому и решения могут получиться приблизительными;

Чтобы проверить точность полученных решений, их нужно подставить в уравнения системы!

Задания для групповой работы :

• Группа №1: Решите графически систему уравнений:

Группа №2: Решите графически систему уравнений:

• Группа №3: Решите графически систему уравнений:
• Дополнительно: №525

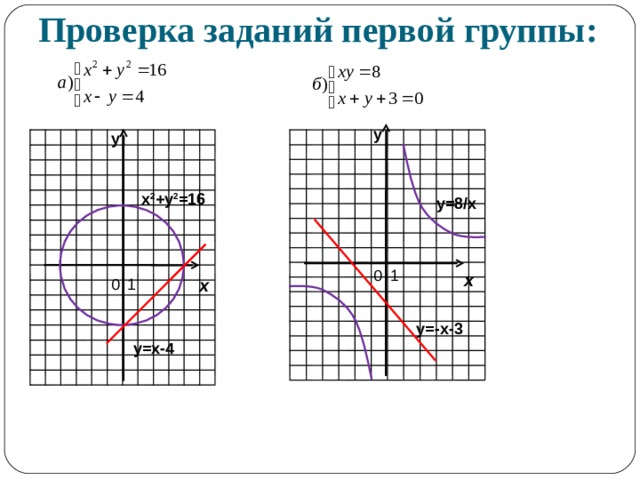
Проверка заданий первой группы:

у

у

х 2 +у 2 =16

y=8/x

х

х

y=-x-3

у=х-4

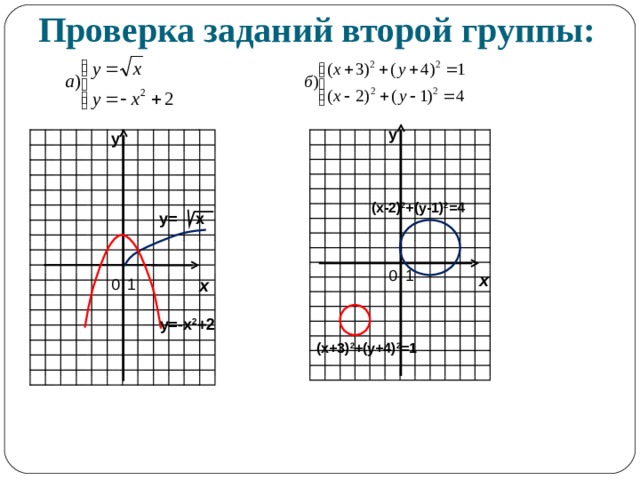
Проверка заданий второй группы:

у

у

(х-2) 2 +(у-1) 2 =4

у= х

х

х

у=-х 2 +2

(х+3) 2 +(у+4) 2 =1

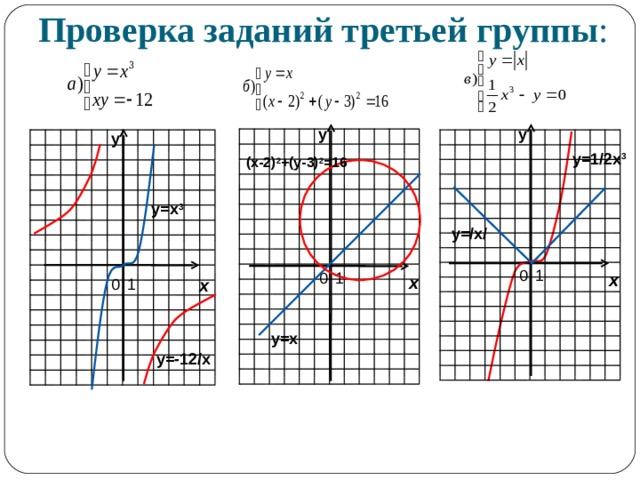
Проверка заданий третьей группы :

у

у

у

у=1/2х 3

(х-2) 2 +(у-3) 2 =16

у=х 3

у=/х/

х

х

х

у=х

y= -12 /x

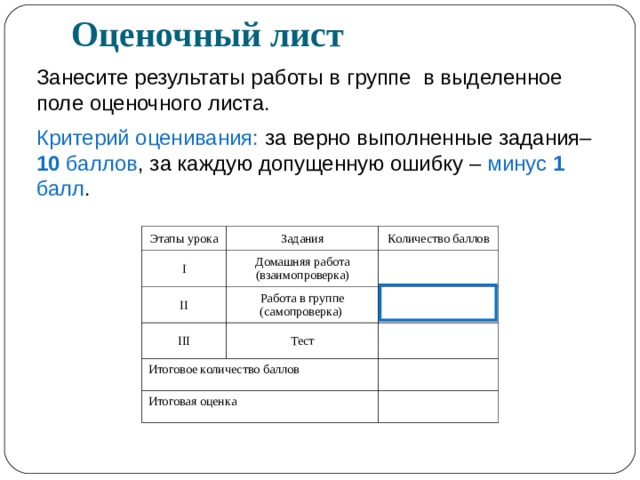
Оценочный лист

Занесите результаты работы в группе в выделенное поле оценочного листа.

Критерий оценивания: за верно выполненные задания– 10 баллов , за каждую допущенную ошибку – минус 1 балл .

Этапы урока

I

Задания

Количество баллов

Домашняя работа (взаимопроверка)

II

III

Работа в группе (самопроверка)

Итоговое количество баллов

Тест

Итоговая оценка

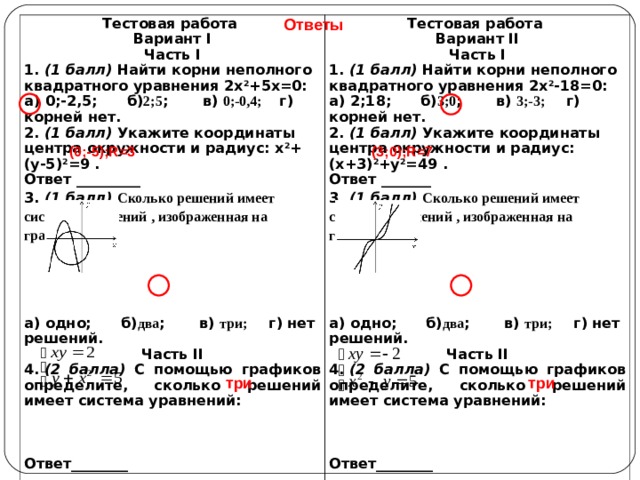
Ответы

Тестовая работа

Вариант I

Часть I

1.  (1 балл) Найти корни неполного квадратного уравнения 2х 2 +5х=0:

а) 0;-2,5; б) 2;5 ; в) 0;-0,4; г) корней нет.

2.  (1 балл) Укажите координаты центра окружности и радиус: х 2 +(у-5) 2 =9 .

Ответ ___ ______

3.  (1 балл) Сколько решений имеет система уравнений , изображенная на графике:

Тестовая работа

Вариант II

Часть I

1.  (1 балл) Найти корни неполного квадратного уравнения 2х 2 - 18=0:

а) 2;18; б) 3;0 ; в) 3;-3; г) корней нет.

2.  (1 балл) Укажите координаты центра окружности и радиус: (х+3) 2 +у 2 =49 .

Ответ _______

3.  (1 балл) Сколько решений имеет система уравнений , изображенная на графике:

а) одно; б) два ; в) три; г) нет решений.

Часть II

4.  (2 балла) С помощью графиков определите, сколько решений имеет система уравнений:

Ответ________

а) одно; б) два ; в) три; г) нет решений.

Часть II

4.  (2 балла) С помощью графиков определите, сколько решений имеет система уравнений:

Ответ________

(0 ;-5); R=3

(3 ; 0 ); R=7

три

три

Оценочный лист

Занесите результаты теста в выделенное поле оценочного листа.

Критерий оценивания: Количество баллов за каждое верно выполненное задание указано в тесте.

Подсчитаем итоговое количество баллов.

Этапы урока

I

Задания

Количество баллов

Домашняя работа (взаимопроверка)

II

III

Работа в группе (самопроверка)

Итоговое количество баллов

Тест

Итоговая оценка

1.Что называется решением системы уравнений с двумя переменными?

2.С каким способом решения систем уравнений с двумя переменными мы познакомились?

3.В чём заключается его суть?

4.Дает ли данный способ точные результаты?

5.В каком случае система не будет иметь решений?

Домашнее задание:

• № 417, № 523
• Д о п о л н и т е л ь н о: № 526.