Геометрия Земли

Презентация на тему: Геометрия Земли

Выполнила: Ученица 10”A”класса МОУ”СОШ”№52 Лыкова Полина Учитель: Степухина Галина Евгеньевна Предмет: математика

ПАРАЛЛЕЛИ И МЕРИДИАНЫ

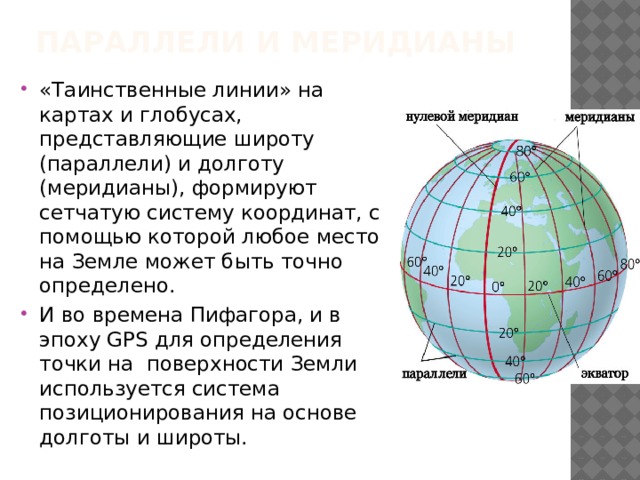
• «Таинственные линии» на картах и глобусах, представляющие широту (параллели) и долготу (меридианы), формируют сетчатую систему координат, с помощью которой любое место на Земле может быть точно определено.
• И во времена Пифагора, и в эпоху GPS для определения точки на поверхности Земли используется система позиционирования на основе долготы и широты.

Что такое широта?

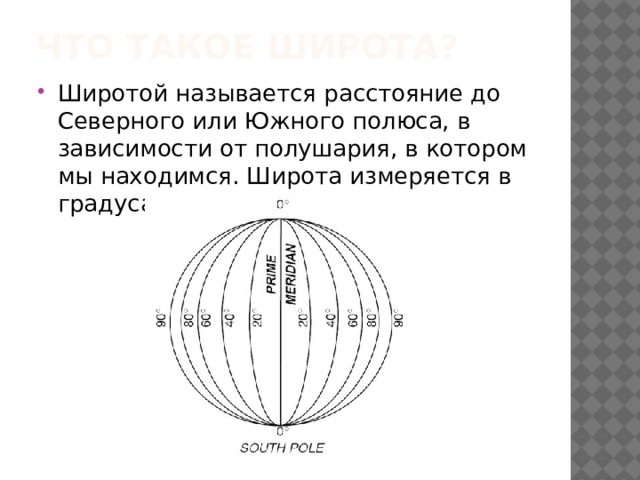
• Широтой называется расстояние до Северного или Южного полюса, в зависимости от полушария, в котором мы находимся. Широта измеряется в градусах от экватора.

Что такое долгота?

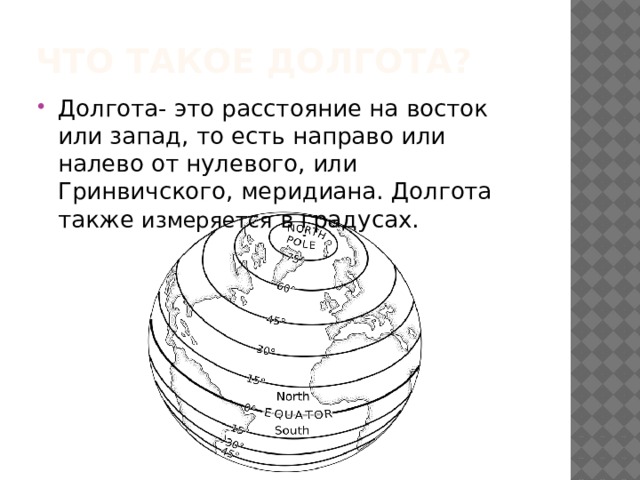
• Долгота- это расстояние на восток или запад, то есть направо или налево от нулевого, или Гринвичского, меридиана. Долгота также измеряется в градусах.

Почему широта и долгота измеряются в градусах, а не в километрах?

Для начала заметим, что поверхность, на которой производятся расчеты, является сферой , которая не имеет третьего измерения и является двухмерной поверхностью. Значит, чтобы отметить точку на ней, нам нужны только две координаты.

• Представьте себе круг, разделенный на 360°. Если через центр провести две перпендикулярные линии, то получатся 4 круговых сектора. Проводя таким образом еще линии, будем получать сектора меньшего размера. Их дуги характеризуются размером угла. Это значит, что угловые измерения применимы к любой точке окружности.

Почему широта и долгота измеряются в градусах, а не в километрах?

• Теперь представьте себе не круг, а сферу, такую как Земля. Если ее разделить на две части от одного полюса к другому, то можно использовать угловые измерения, так же как в круге, и, следовательно, можно определять положение точки по угловым значениям широты и долготы.

Почему широта и долгота измеряются в градусах?

• Если посмотреть на глобус, то можно заметить, что все меридианы имеют одинаковую длину, тогда как параллели - разную. Самой длинной параллелью является сам экватор, длина которого около - 40 000 км. Причем чем ближе к полюсам, тем параллели становятся короче. На северном и южном полюсах широта превращается просто в точку, с координатами 90 север.широты и 90 юж.широты. Что удивительно – только эти два места на всей Земле не имеют долготы.

Сколько же километров в одном градусе?

• Градус широты составляет приблизительно 111 километров, минута широты составляет приблизительно 1,85 километров. Секунда широты составляет приблизительно 0,03 километра, или примерно 30 метров. Градус долготы изменяется по расстоянию. На экваторе это - приблизительно 111 километров, тоже самое расстояние, как и градус широты.

Сколько же километров в одном градусе?

• Размер долготы постепенно уменьшается и стремится к нулю, поскольку меридианы сходятся на полюсах Земли. Так, на широте 45° градус долготы составляет приблизительно 79  километров. Поскольку, градус долготы изменяется по размеру, минуты и секунды долготы также изменяются, уменьшаясь по размеру к полюсам.

Как найти кратчайшее расстояние между Барселоной и Токио?

• Барселона:2° восточ. долготы и 41° север. широты.
• Токио: около 140° восточ. долготы и 36° север. широты.
• Рассмотрим сферический треугольник ABD.

Как найти кратчайшее расстояние между Барселоной и Токио?

• d - геодезическая линия от Барселоны к Токио – минимальное расстояние между городами. По

теореме косинусов для сферических треугольников:

Чтобы вычислить b и a , возьмем экватор за горизонтальную ось и вычтем из 90° широту каждой точки. Для нахождения угла D - в качестве оси координат Гринвичский меридиан: a = 90°-41°=49° и b= 90°-36°=54°, D=140 °-2°=138°.

Подставляя эти данные в теорему косинусов, получим: cos d=-0,0681225162. Откуда, d=93,90614266 °. Учитывая , что R (Земли)=6 350км, длина окружности большого круга на поверхности земного шара: 2π R=39 898,23км. Итак, угол d=93,90614266 ° соответствует 10 407,46911км .Мы получили расстояние между Барселоной и Токио.

Современные технологии

• Современные технологии позволяют рассчитывать расстояния быстро и с большей точностью. Мы рассчитали расстояние от Барселоны до Токио вручную, но пожалуй, самое удивительное, что этот результат может быть получен лишь с помощью координат на карте мира.
• Компьютерные программы позволяют вычислять расстояния между конкретными точками, например, между конкретными зданиями на той или иной улице. Использование компьютеров породило новую область геометрии под названием вычислительная геометрия.

Вывод:

• Нам проще измерять долготу и широту в градусах, т.к. там мы будем лучше знать местонахождение города(страны и т.д.) А если нужно рассчитать километраж, то можно воспользоваться специальными формулами или программами.

Заключение:

• Заканчиваю рассказ о геометрии Земли классическим описанием сферы из диалога Платона «Тимей, или О природе»: «По такой причине Бог построил во всем его разнообразии единое целое, совершенное и непричастное дряхлению и недугам. Что касается формы целого, то ему подобают такие очертания, которые содержат в себе все другие. Именно поэтому Он округлил Землю до состояния сферы, поверхность которой повсюду равно отстоит от центра. Эти очертания из всех очертаний наиболее совершенные и подобные самим себе, потому что подобное он нашел в мириады раз более прекрасным, чем неподобное».

Использована литература:

• Мир математики: в 40т. Т.4: Ж.Гомес. Когда прямые искривляются. Неевклидовы геометрии./Пер.с англ. – М.: Де Агостини, 2014.-160с.
• Мир математики: в 45т. Т.38: Иоланда Гевара. Карлес Пюиг. Измерение мира. Календари,меры длины и математика./Пер.с исп. – М.: Де Агостини, 2014.-160с.
• http://www.m-globe.ru/index.html
• https://www.google.ru/search?q=%D0%B7%D0%B5%D0%BC%D0%BB%D1%8F+%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8&newwindow=1&biw=1920&bih=935&tbm=isch&tbo=u&source=univ&sa=X&ved=0ahUKEwjt4uGNvcXJAhUF7HIKHUD2CVwQsAQIGg&dpr=1