Получите свидетельство
Вход
Цели урока:
-систематизировать знания учащихся о взаимном расположении точек и прямых;
-познакомить учащихся со свойством прямой (через любые две точки можно провести прямую и притом только одну);
-рассмотреть прием практического проведения прямых на плоскости.
План урока.
Организационный момент
Вводная беседа
Изучение нового материала
Закрепление изученного материала
Домашнее задание.
Ход урока.
1. Организационный момент.
Сообщение темы урока и формулирование целей.
2. Вводная беседа.
Учащимся раздается лист содержащий следующий текст. Потом задаются вопросы по тексту.
Геометрия – одна из наиболее древних наук. Первые геометрические сведения найдены в вавилонских клинописных таблицах и египетских папирусах (3 тысячелетие до н. э. ), а также в других источниках.
Название науки «геометрия» древнегреческого происхождения, оно составлено из двух древнегреческих слов: «ge»-«земля» и «metreo»-«измеряю»(измеряю землю). Появление и развитие геометрических знаний связанно с практической деятельностью людей.
Это отразилось и в названии многих геометрических фигур. Например название фигуры трапеция происходит от греческого слова «trapezion»- столик, от которого произошло также слово- трапеза. Термин линия возник от латинского linum- л»ен, льняная нить».
Практические потребности людей (сооружение жилищ, храмов, желание украсить одежду, рисовать картины) способствовали приобретению и накоплению геометрических сведений, которые изначально передавались в устной форме из поколения в поколение.
Новые сведения и факты добывались опытным путем, выводились некоторые правила (например правила вычисления площадей) и данная наука не являлась точной. И только в 6 веке до нашей эры древнегреческий ученый Фалес начал получать новые геометрические сведения с помощью доказательств.
В 3 веке до нашей эры греческий ученый Евклид написал сочинение «Начала» и почти два тысячелетия геометрия изучалась по этой книге, а наука в честь ученого была названа евклидовой геометрией. (Слайд 3, 4, 5)
В настоящее время геометрия – это целая наука, занимающаяся изучением геометрических фигур. (Слайд 6)
Далее целесообразно продолжить беседу, опираясь на ранее полученные знания в курсе математики 1-6 классов, в виде ответов на вопросы:
-Какие геометрические фигуры вам известны?
Далее включаем слайд на котором фигуры разделены на два столбика. (Слайд 7)
-По какому принципу данные геометрические фигуры записаны в две группы?
Часть геометрии, в которой рассматриваются фигуры на плоскости, называется планиметрией, а та часть, в которой рассматриваются фигуры в пространстве называется стереометрией. Мы начинаем изучение геометрии с планиметрии. Записывается информация со слайда в тетрадь.
3. Изучение нового материала.
В курсе математики учащиеся уже знакомы с понятиями прямая, отрезок, умеют их обозначать, чертить, знают о принадлежности точек прямой и отрезку, поэтому нет необходимости повторять уже известные факты. Будет целесообразнее организовать повторение данной темы в ходе выполнения следующих упражнений при параллельном введении новых понятий, определений и т. д.
К доске вызывается один из учащихся, остальные работают в тетрадях. Учитель читает задание и по мере необходимости вводит новые понятия, символы, делает необходимые записи на доске.
Начертите прямую. Как ее можно обозначить? (Прямая а или АВ)
Отметьте точку С, не лежащую на данной прямой. И точки Д, Е, К, лежащие на этой прямой.
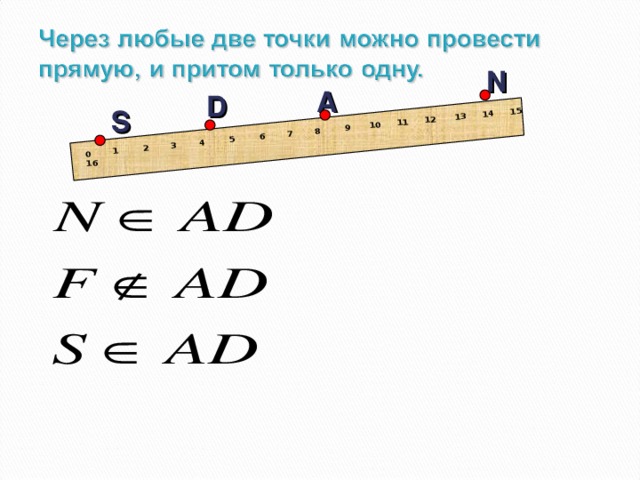
В математике существуют специальные символы, позволяющие кратко записать как5ое либо утверждение. Символы € не принадлежит. (Слайд 8)
Сколько прямых можно провести через две точки?(одну прямую)
Через любые две точки можно провести прямую?(да, и притом только одну)
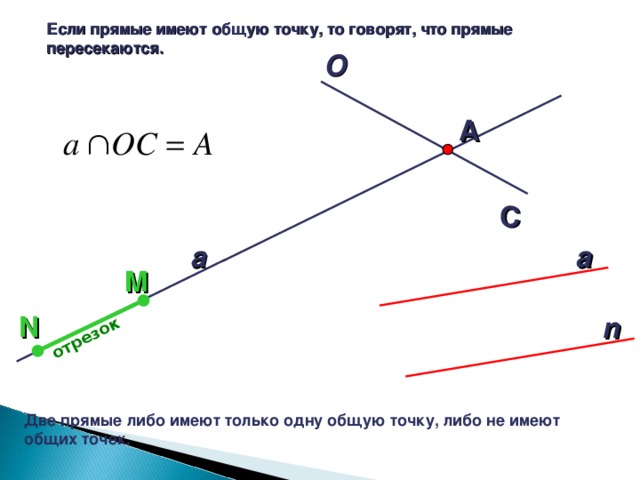
Начертите прямые XY и MK, пересекающиеся в точке О. Для того чтобы кратко записать, что прямые XY и MK, пересекаются в точке О, используют символ ∩ и записывают так: XY∩MK=0. . (Слайд 9)
Сколько общих точек могут иметь две прямые? (Две прямые могут иметь или одну общую точку или не иметь ни одной.
На прямой a отметьте последовательно точки А, В, С, D. Запишите все получившиеся отрезки(получились отрезки АВ, ВС, CD, AC, AD, BD. ) (работа у доски)
4. Закрепление изученного материала.
Можно предложить задания для самостоятельного решения.
1 уровень
Учебник: задачи № 2, 5, 6. (Слайд 10)
2 уровень
Решить задачи.
Сколько точек пересечения могут иметь три прямые? Рассмотрите все возможные случаи и сделайте рисунки. Ответы: три точки пересечения, одна точка пересечения, 2 точки пересечения, ни одной точки пересечения. )
На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки(Ответы:1 прямая, 3 прямые)
В ходе самостоятельного решения учителю желательно контролировать работу учащихся, решающих задачи 1 уровня сложности с целью проверки успешности усвоения темы урока и своевременной помощи при возникающих у учащихся затруднениях.
В конце урока заслушать учащихся выполняющих задачи 2 уровня сложности, выполнив на доске необходимые рисунки. При этом учитель должен обратить внимание на то, чтобы учащиеся, не решавшие данные задачи поняли суть решения.
Домашнее задание.
№1, №3, №7, №4. (Слайд 11)
Параграф 1-2, вопросы 1-3 стр. 25. Подготовить сообщение об «истории геометрии».
Подведение итогов урока: Выставление оценок за работу на уроке.
Конспект урока и презентация по математике "Первоначальные геометрические сведения" (2.27 MB)
0
557
82
Нравится
0
