Геометрия. Презентация

Тема : Пирамида

• Определение пирамиды;
• Виды пирамид;
• Площадь полной поверхности пирамиды;
• Правильная пирамида;
• Свойства правильной пирамиды;
• Усечённая пирамида;
• Формулы площадей поверхности и объём пирамиды

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Достаточно вспомнить знаменитые египетские пирамиды и самую известную из них – пирамиду Хеопса (XXVII в до н.э.) .

Это правильная пирамида, в основании которой квадрат со стороной 233 м и высота которой достигает 146,5 м. Не случайно говорят, что пирамида Хеопса – немой трактат по геометрии.

Церковь в Каменском

Современный стеклянный вход в Лувр, который появился во дворе ренессансного дворца 20 лет назад и до сих пор остается спорным новоделом, — это тоже многогранник, пирамида.

Вот так выглядит здание публичной библиотеки в Сиэтле (США).



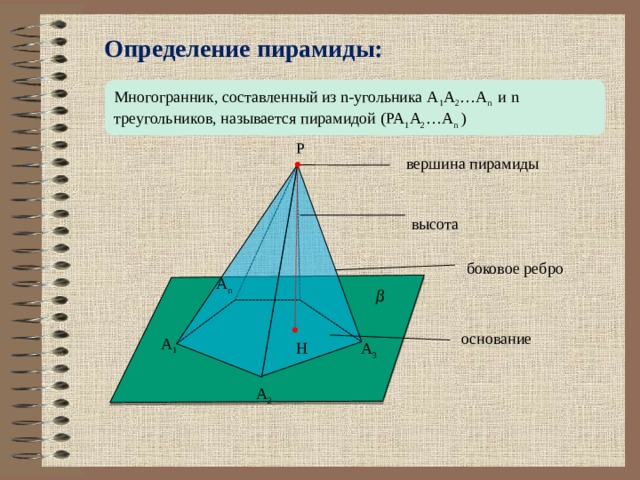
Определение пирамиды:

Многогранник, составленный из n-угольника A 1 A 2 …A n и n треугольников, называется пирамидой (PA 1 A 2 …A n )

P

вершина пирамиды

высота

боковое ребро

A n

основание

A 1

H

A 3

A 2

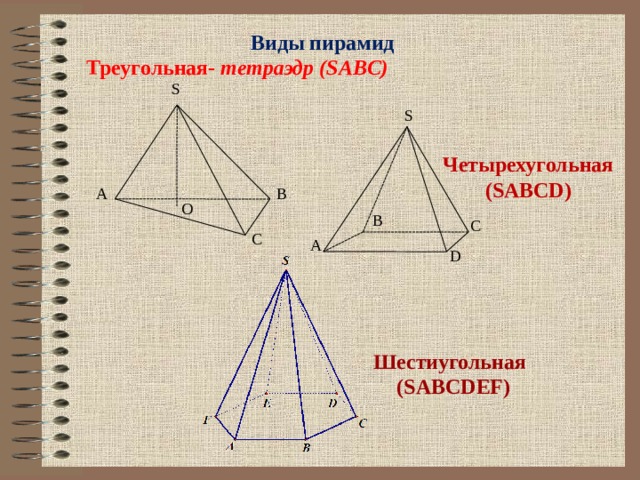
Виды пирамид

Треугольная- тетраэдр (SABC)

S

S

Четырехугольная (SABCD)

B

А

O

B

C

C

A

D

Шестиугольная (SABCDEF)

Площадью полной поверхности пирамиды называется сумма площадей всех её граней:

S полн. =S бок. +S осн.

12

Практическое задание.

Письменно ответить на вопросы:

На следующем слайде изображены пирамиды.

1. Назовите пирамиды, изображённые на рисунках.

2. Назовите вид изображенных пирамид.

3. Что является основанием каждой пирамиды, назовите их?

4. Назовите боковые грани пирамид?

S

S

M

B

C

C

N

O

Д

A

P

A

O

M

h

D

G

C

N

A

G 1

B

H

C

B

15

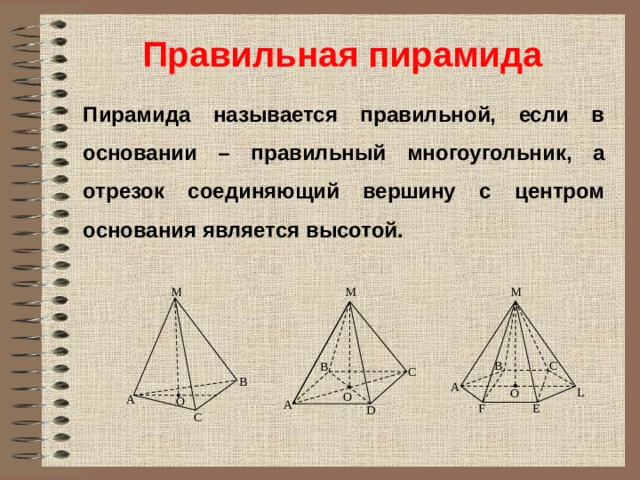
Правильная пирамида

Пирамида называется правильной, если в основании – правильный многоугольник, а отрезок соединяющий вершину с центром основания является высотой.

М

M

М

С

B

B

С

В

A

L

O

O

А

О

А

E

F

D

С

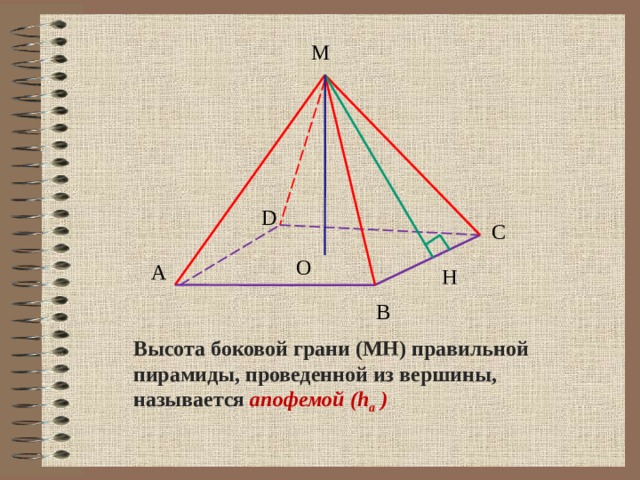
М

D

C

O

A

H

B

Высота боковой грани (МН) правильной пирамиды, проведенной из вершины, называется апофемой (h a )

17

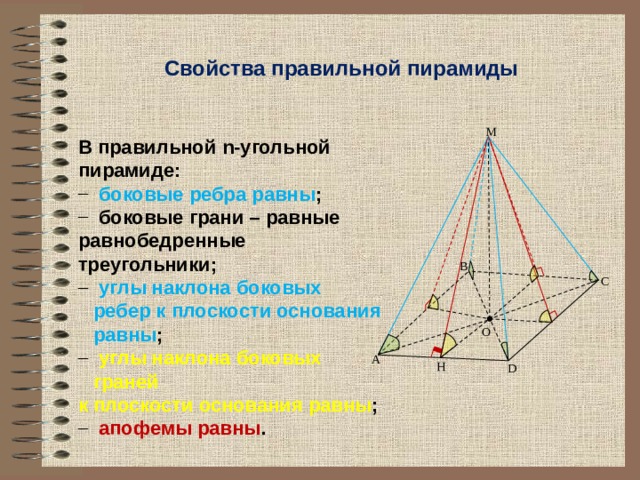
Свойства правильной пирамиды

M

В правильной n-угольной пирамиде:

• боковые ребра равны ;
• боковые грани – равные

равнобедренные треугольники;

• углы наклона боковых ребер к плоскости основания равны ;
• углы наклона боковых граней

к плоскости основания равны ;

• апофемы равны .

B

C

O

A

H

D

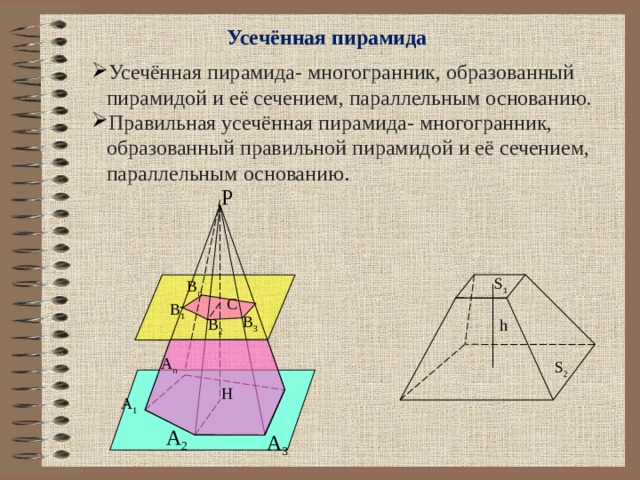
Усечённая пирамида

• Усечённая пирамида- многогранник, образованный пирамидой и её сечением, параллельным основанию.

• Правильная усечённая пирамида- многогранник, образованный правильной пирамидой и её сечением, параллельным основанию .

P

S 1

B n

C

B 1

B 3

B 2

h

A n

S 2

H

A 1

A 2

A 3

Усечённая пирамида применяется при изготовлении некоторых строительных конструкций

19

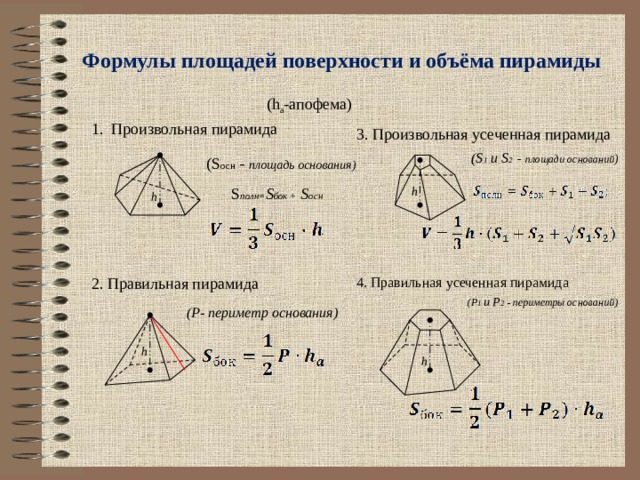
Формулы площадей поверхности и объёма пирамиды

(h a -апофема)

1. Произвольная пирамида

3. Произвольная усеченная пирамида

(S 1 и S 2 - площади оснований )

(S осн - площадь основания)

h

S полн= S бок + S осн

h

2. Правильная пирамида

4. Правильная усеченная пирамида

(P 1 и P 2 - периметры оснований)

(Р- периметр основания)

h

h

Спасибо за внимание

УДАЧИ!