Конспект урока по теме: «Геометрическая прогрессия»
Цель: 1) Продолжить изучение темы геометрическая прогрессия. Познакомить учащихся с Формулой суммы n-первых членов геометрической прогрессии.
2) Развивать умение анализировать, сопоставлять. Развивать умение критически оценивать результат своего действия и действия других.
3) Воспитывать аккуратность, умение организовать себя на урок.
Тип урока: «Комбинированный урок с элементами технологии развивающего обучения, ТРКМ, проблемного обучения.
План.
1. Организационный момент
2. Домашнее задание.
3. Актуализация опорных знаний.
4. Изучение нового материала.
5. Физкультминутка.
6. Закрепление.
7. Итог.
Ход урока.
1. Организационный момент. Приветствие учащихся.
2.Домашнее задание. № 17.25в; 17.26в; 17.28в, г; 17.30.
3. Актуализация опорных знаний:
а) Установите закономерность и определите число, стоящее в пустой клетке.
| 2 | 3 | 4 |
|
|
|
|
| 32 | 243 |
|
|
|
|
б)Установи закономерность в расположении геометрических фигур и составь определение.
Геометрическая прогрессия- это числовая последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и тоже число.
После получения определения, учащиеся формулируют тему урока.
в) Найти ошибку:
1) Числовая последовательность 1,6; 0,8; … является геометрической прогрессией найти первый член прогрессии и знаменатель геометрической прогрессии.
Ответ: b1 = 0,8 q = 2.
2) 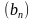 – геометрическая прогрессия ; b1 = 3,2; q =
– геометрическая прогрессия ; b1 = 3,2; q = 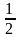 . Найти b2 .
. Найти b2 .
Ответ: 6,4.
3) (bn) – геометрическая прогрессия b5 = 11; b7 = 99. Найти знаменатель геометрической прогрессии.
Ответ: 9.
в) Расположите ответы в порядке возрастания и вы узнаете имя древнегреческого ученого, который занимался вычислением сумм прогрессий.
1) (bn) – геометрическая прогрессия. Найти b4 , если b1 = 2; q = 3. (Д)
( 54)
2) (bn) – геометрическая прогрессия. Найти b2 , если b1 = 128; q = 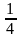 . (Е)
. (Е)
( 32)
3) (bn) – геометрическая прогрессия. Найти b1 , если b5 = 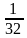 ; q =
; q = 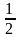 . (А)
. (А)
( 0,5)
4) (bn) – геометрическая прогрессия. Найти следующий член прогрессии
0,2; 0,8; … . (Х)
( 3,2)
5) (bn) – геометрическая прогрессия. Найти q, если b2 = 32; b1 = 16. ( Р)
( 2)
6) Поставьте между числами 3 и 81 два числа, чтобы вместе с данными
числами получилась геометрическая прогрессия. (И; М)
( 9; 27)
Ответ: Архимед.
Древнегреческий ученый Архимед неоднократно в своих трудах возвращался к вопросу о вычислении сумм прогрессий. В трактате «О квадратуре параболы» он рассматривает задачу, эквивалентную задаче о нахождении суммы бесконечной убывающей прогрессии.
4. Изучение нового материала.
По приданию индийский царь Шерам, восхищенный игрой в шахматы, призвал к себе изобретателя игры Сету и сказал: «Я желаю достойно наградить тебя за прекрасную игру. Я достаточно богат, чтобы исполнить любое твое желание. Сета попросил царя положить на первую клетку шахматной доски одно зерно, на вторую клетку два зерна, на третью клетку четыре зерна и т.д.
Смог ли царь Шерам выполнить желание Сеты?
Вывод формулы Sn .
Пусть (bn) – геометрическая прогрессия.
Sn = b1 + b2 + b3 + … + bn |∙q
Sn ∙ q = b1q + b2q + … + bnq
Sn ∙ q = b2 + b3 + … + bnq
Sn ∙ q – Sn = (b2 + b3 + … + bnq) – (b1 + b2 + b3 + … + bn)
Sn(q – 1) = b2 + b3 + … + bnq – b1 – b2 – b3 – … – bn
Sn(q – 1) = bnq – b1)
Sn = 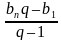 , где q
, где q 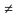 1 Формула суммы n – первых членов геометрической прогрессии.
1 Формула суммы n – первых членов геометрической прогрессии.
bn = b1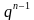 ; Sn =
; Sn = 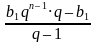 =
= 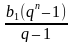
Sn = 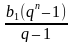 , где q
, где q 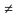 1 Формула суммы n – первых членов геометрической прогрессии.
1 Формула суммы n – первых членов геометрической прогрессии.
Эта формула встречается в « Началах» Евклида ( 3 в до н. э.)
Итак, с помощью полученной формулы, ответим на вопрос: «Смог ли царь Шерам выполнить желание Сеты»
Дано: Решение
( bn ) – геом. пр. Sn =
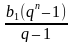 ;
;
b1 = 1 S64 = 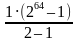 = 264 – 1 = 18 446 470 073 709 551 615
= 264 – 1 = 18 446 470 073 709 551 615
q = 2
S64 – ?
18 квинтиллионов 446 квадриллионов 744 триллиона 73 миллиарда 709 миллионов 551 тысяча 615
Л.Н.Толстой, заинтересованный этой легендой, рассчитал количество зерен предназначавшихся Сете. Данное количество зерен соответствует 230 584 300 921 369 пудов. Такое количества зерна еще не собранно человечеством до нашего времени.
5. Физкультминутка
6. Закрепление.
1) Найти сумму шести первых членов геометрической прогрессии (bn), в которой b1 = 3; q = 2.
2) Найти сумму пяти первых членов геометрической прогрессии 1,5; – 3 … .
Дано: Решение
( bn ) – геом. пр. Sn =
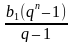 ;
;
b1 = 3 S6 = 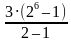 =
= 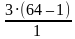 = 3 ∙ 63 = 189
= 3 ∙ 63 = 189
q = 2
S6 – ? Ответ: 189
Дано: Решение
( bn ) – геом. пр. Sn =
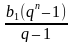 ; b1 = 1,5; q =
; b1 = 1,5; q = =
=
= – 2
(bn): 1,5; – 3; … S6 = = = – 0,5 ∙ (– 33) = 16,5
S5 – ? Ответ: 16,5
Взаимоконтроль, взаимооценка.
7. Итог:
а) Верные и неверные утверждения.
1) Верно ли, что каждый член геометрической прогрессии равен предыдущему члену умноженному на одно и то же число?
2) Верно ли, что bn = b1 – формула n – го члена геометрической прогрессии?
3) Верно ли, что модуль любого члена геометрической прогрессии равен среднему геометрическому предыдущего и последующего членов?
4) Верно ли, что q = – формула знаменателя геометрической прогрессии?
5) Верно ли, что геометрическую прогрессию можно рассматривать как показательную функцию заданную на множестве натуральных чисел?
6) Верно ли, что Sn = – формула суммы n – первых членов геометрической прогрессии?
7) Верно ли, что числовая последовательность 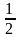 ;
; 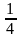 ;
; … является геометрической прогрессией?
б) Самооценка.
| Устная работа | Зашифрованное задание | Решение задач | Верные и неверные утверждения | Итоговая оценка |
|
|
|
|
|
|
Итоговая отметка – это среднее арифметическое отметок, выставленных за
работу на уроке.
Учитель подводит итог урока, используя лист самооценки.

 Получите свидетельство
Получите свидетельство Вход
Вход


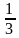
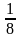
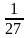
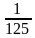









 Геометрическая прогрессия (25.02 KB)
Геометрическая прогрессия (25.02 KB)
 0
0 385
385 10
10 Нравится
0
Нравится
0






