Определения.
Геометрическое место – термин, применявшийся в старой литературе по геометрии и до сих пор применяющийся в учебной литературе, для обозначения множества точек, удовлетворяющих некоторому условию, как правило, геометрического характера.
Например: геометрическое место точек, равноудаленных от двух данных точек A и B – это серединный перпендикуляр к отрезку AB. Иногда говорят и о геометрическом месте прямых и других фигур.
Название связано с представлением о линии как о «месте», на котором располагаются точки.
Геометрическое Место Точек (ГМТ) - в геометрии траектория некоторой точки, перемещающейся в соответствии с данной формулой или условием. Например, круг является геометрическим местом точки, перемещающейся на плоскости так, что расстояние от места ее нахождения до центра остается неизменным.
Геометрическое место точек (ГМТ) - это множество точек, в которое попадают все точки, удовлетворяющие определенному условию, и только они.
Геометрическое место точек (ГМТ) - фигура речи в математике, употребляемая для определения геометрической фигуры как множества точек, обладающих некоторым свойством.
Примеры.
Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудалённых от концов отрезка.
Окружность есть геометрическое место точек, равноудалённых от данной точки, называемой центром окружности.

Парабола есть геометрическое место точек, равноудалённых от точки (называемой фокусом) и прямой (называемой директрисой).
Пример 1.
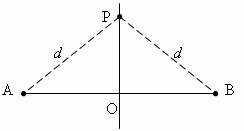
Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка. Пусть PO перпендикулярно AB и AO = OB:
Тогда, расстояния от любой точки P, лежащей на срединном перпендикуляре PO, до концов A и B отрезка AB одинаковы и равны d.
Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.
Пример 2.
Биссектриса угла есть геометрическое место точек, равноудалённых от его сторон.
Пример 3.
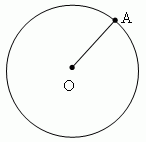
Окружность есть геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра (на рис. показана одна из этих точек – А).
Окружность.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход


 Окружность
Окружность








 Геометрическое место точек (методический материал) (25.3 КB)
Геометрическое место точек (методический материал) (25.3 КB)
 0
0 2862
2862 135
135 Нравится
0
Нравится
0







