Задачи ЕГЭ по информатике
Система логических уравнений (B23)
Пример 1.
Сколько существует различных наборов значений логических переменных x1, ..., x6, y1, ..., y6, которые удовлетворяют всем перечисленным ниже условиям?
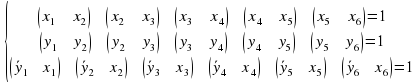
Решение:
Поскольку, 1 и 2 уравнения идентичны, найдем все решения уравнения 1:
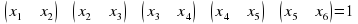
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | |||||
| 1 | 1 | ||||
| 1 | 1 | 1 | |||
| 1 | 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
Всего данное уравнение имеет 7 решений.
Так же и второе уравнение имеет 7 решений.
Два уравнения без третьего имеют 7*7 = 49 решений.
Составим таблицы решений равнения 1 и 2:
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 |
| y1 | y2 | y3 | y4 | y5 | y6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Рассмотрим какие ограничения в решение системы наложит третье уравнение:
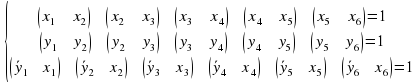
Возьмем первое решение х1..х6 и найдем какие решения y1..y6 соответствуют системе
Чтобы найти решение, мы складываем xi и не( yi ), которые в сумме должны дать 1
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 |
| y1 | y2 | y3 | y4 | y5 | y6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Получается только 1 решение системы
2 решение х1..х6:
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 |
| y1 | y2 | y3 | y4 | y5 | y6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Всего 2 решения системы
3 решение х1..х6:
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 |
| y1 | y2 | y3 | y4 | y5 | y6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Всего 3решения системы
4 решение х1..х6:
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 |
| y1 | y2 | y3 | y4 | y5 | y6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Всего 4 решения системы
5 решение х1..х6:
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 |
| y1 | y2 | y3 | y4 | y5 | y6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Всего 5 решений системы
6 решение х1..х6:
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 |
| y1 | y2 | y3 | y4 | y5 | y6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Всего 6 решений системы
7 решение х1..х6:
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 |
| y1 | y2 | y3 | y4 | y5 | y6 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Всего 7 решений системы
Суммируем полученное количество решений:
1+ 2 + 3 +4 + 5 +6 +7 = 28
Ответ: 28
Пример 2.
Сколько существует различных наборов значений логических переменных x1, ..., x6, y1, ..., y6, которые удовлетворяют всем перечисленным ниже условиям?
Поскольку, 1 и 2 уравнения идентичны, найдем все решения уравнения 1:
| Х1 | Х2 | Х3 | Х4 | Х5 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | ||
| 1 | 1 | |||
| 0 | ||||
| 0 | 0 | 0 | 0 |
Всего данное уравнение имеет 6 решений.
Так же и второе уравнение имеет 6 решений.
Два уравнения без третьего имеют 6*6 = 36 решений.
Составим таблицы решений уравнений 1 и 2:
| Х1 | Х2 | Х3 | Х4 | Х5 |
| y1 | y2 | y3 | y4 | y5 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Рассмотрим какие ограничения в решение системы наложит третье уравнение:
Возьмем первое решение х1..х6 и найдем какие решения y1..y6 соответствуют системе
Чтобы найти решение, мы складываем xi и не( yi ), которые в сумме должны дать 1, если все суммы равны 1, то их произведение равно 1.
| Х1 | Х2 | Х3 | Х4 | Х5 |
| y1 | y2 | y3 | y4 | y5 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Всего 1 решение системы
2 решение х1..х6
| Х1 | Х2 | Х3 | Х4 | Х5 |
| y1 | y2 | y3 | y4 | y5 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Всего 2 решения системы
3 решение х1..х6
| Х1 | Х2 | Х3 | Х4 | Х5 |
| y1 | y2 | y3 | y4 | y5 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Всего 3 решения системы
4 решение х1..х6
| Х1 | Х2 | Х3 | Х4 | Х5 |
| y1 | y2 | y3 | y4 | y5 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Всего 4 решения системы
5 решение х1..х6
| Х1 | Х2 | Х3 | Х4 | Х5 |
| y1 | y2 | y3 | y4 | y5 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Всего 5 решений системы
6 решение х1..х6
| Х1 | Х2 | Х3 | Х4 | Х5 |
| y1 | y2 | y3 | y4 | y5 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Всего 6 решений системы
Суммируем полученное количество решений:
1+2 + 3 +4 + 5 +6 = 21
Ответ: 21
Задачи для самостоятельной работы:
Сколько различных решений имеет система уравнений?
(x1 x2) (x2 x3) (x3 x4) (x4 x5) (x5 x6) = 1
(у2 у1) (у3 у2) (у4 у3) (у5 у4) (у6 у5) = 1
y1 x2 = 1
где x1,x2,…,x6, у1,у2,…,у6 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
(ответ: 19)
Сколько различных решений имеет система уравнений?
(x1 x2) (x2 x3) (x3 x4) (x4 x5) (x5 x6)=1
(у1 у2) (у2 у3) (у3 у4) (у4 у5) (у5 у6)=1
(z1 z2) (z2 z3) (z3 z4) (z4 z5) (z5 z6)=1
x6 у6 z6 = 0
где x1,x2,…,x6, у1,у2,…,у6, z1,z2,…,z6 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
(ответ: 127)

 Получите свидетельство
Получите свидетельство Вход
Вход
































 Методика решения систем уравнений (103.38 KB)
Методика решения систем уравнений (103.38 KB)
 0
0 726
726 31
31 Нравится
0
Нравится
0









