Функция у=k/x и её график

Оборудование: Плакат с кроссвордом, на доске приготовлены 2 таблицы, таблица с графиками функций, координатная плоскость.

Ход урока. Урок начинается с повторения. Учащимся предлагается разгадать кроссворд, который заранее подготовлен на доске – смотри архив  После того как кроссворд разгадан, учитель задаёт  классу вопрос: «Какие основные способы задания функции нам известны?» Ответ: «Формулой, с помощью графика или таблицы».

Один учащийся получает задание у доски: «Заполнить  таблицу (табл. 1 и табл. 2) значений функции y= 12/x по данным значениям её аргумента».

Таблица 1.

Таблица 2.

Пока вызванный к доске ученик работает, весь класс отвечает на вопросы, которые предъявляются в виде таблицы.

                               Вопросы.

Как называются следующие функции, заданные формулами:  y =- kx, y = kx + b, y = x², y = kx²,  y = x³, y = kx³?

Укажите области определения следующих функций:  y = x² + 8, y = 1/(x – 7), y = (4x – 1)/5, y = 2x, y=7 – 5x, y=2/x, y= x³, y= -10/x.

После фронтального разбора вопросов внимание класса привлекается к ученику, работающему у доски. Все вместе проверяем, верно ли он заполнил таблицы. Следующий ученик выполняет на доске новое задание: «по данным в таблице координатам (x;y) построить на координатной плоскости соответствующие точки».

Ученик приступает к работе, а весь класс занимается по предложенным таблицам, отвечая на вопросы:

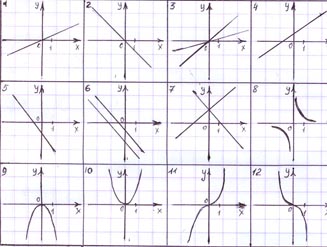
1. На каком рисунке из таблицы изображён график:

а) линейной функции;

б) прямой пропорциональности;

в) квадратичной функции;

г) функции вида  y= kx³?

2. Какой знак имеет коэффициент  k  в формулах вида  y= kx + b, которым соответсвуют  графики рис. 1, 2, 4, 5 таблицы?
3. Найдите в таблице графики линейных функций, у которых угловые коэффициенты: а) равны; б) равны по модулю и противоположны по знаку.

Далее класс проверяет, верно, ли ученик, вызванный к доске, расставил точки на координатной оси.

- Итак, проведено повторение сведений о функциях за 7 класс. Как известно, всякая функция описывает какие-то процессы, происходящие в окружающем нас мире. Рассмотрим, например, прямоугольник со сторонами x и y и площадью 12 см². Известно, что  x*y=12. Но что будет, если начать изменять одну из сторон прямоугольника, допустим сторону длиной  x ? Длину стороны y  можно узнать из формулы  y = 12/x. Если  x  увеличить в 2 раза, то будем иметь  y = 12/(2x),  т.е. сторона y  уменьшиться в 2 раза. Если значение  x  увеличить в 3, 4, 5 …раз, то значение  y  во столько же раз уменьшается. Наоборот, если x  уменьшать в несколько раз , то  y  будет увеличиваться во столько же раз. Поэтому функцию вида y=12/x называют обратной пропорциональностью. В общем виде она записывается так: y=k/x, где k – константа, причём значение k не равно нулю.

Такие функции встречаются очень часто. Все помнят из курса физики закон Ома:  I = U/R. Он гласит, что если напряжение U постоянно, то сила тока  I обратно пропорциональна сопротивлению R проводника. Сходной формулой описан закон  Бойля – Мариотта для идеального газа: если его масса m постоянна, то объём газа V обратно пропорционален его температуре:  V = m/t.

Для функции  y = 12/x,  являющейся частным видом обратной пропорциональности, мы уже записали в табл. 1 и 2 ряд значений аргумента и функции и изобразили соответствующие точки на координатной плоскости.

Как же выглядит график данной функции?

По построенным точкам трудно судить обо всём графике, ведь точки можно соединить как угодно. Давайте попробуем вместе сделать выводы о графике функции, вытекающие из рассмотрения таблицы и формулы.

Вопросы:

1. Какова область определения функции  y=12/x? (Все числа, кроме 0.)
2. Положительны или отрицательны значения y, если: x <0, x>0? (при  x<0 имеем: y<0; x>0 имеем y >0.)
3. Как меняется переменная  y с изменением x? (При x>0: если x  стремится к нулю, то y стремится к бесконечности, если x  стремится к бесконечности, то y стремится к нулю. При x<0: если x стремиться к нулю, то y стремится к минус бесконечности, если x стремится к минус бесконечности, то y стремится к нулю.)

Выводы.

1. Точка (0;0) не принадлежит графику, т.е. он не пересекает ни оси Ox, ни оси Oy.
2. График находится в 1 и в 3 координатных четвертях.
3. Плавно приближается к координатным осям как в 1 координатной четверти, так и в 3, причём он подходит к осям как угодно близко.

Располагая этими сведениями, мы уже можем соединить точки на рисунке (учитель это делает сам на доске) и увидеть график функции  y=12/x целиком.

Полученная кривая называется гиперболой, что в переводе с греческого означает «прохожу через что-либо». Эта кривая была открыта математиками древнегреческой школы примерно в четвёртом веке до н.э. Термин «гипербола» ввёл Аполлоний.

Теперь рядом с графиком функции y=12/x построим график функции y= -12/x. Учащиеся выполняют это задание в тетрадях, а один ученик у доски. Сравнивая оба  графика, что второй занимает 2 и 4 координатные плоскости, а оба они симметричны относительно начала координат. Затем выясняется вопрос: «Как зависит расположение графика гиперболы y=k/x от знака и от значения коэффициента k?». Учащиеся убеждаются, что если  k>0, то график располагается в 1 и 3 координатных четвертях, а если k<0, то во 2 и 4.

Для закрепления  выполняются номера: № 101, № 105

Далее они видят, что чем больше k по абсолютной величине, тем выше над началом координат располагается одна ветвь графика и тем ниже – другая.

Подведение итогов.

Домашнее задание: № 107, повторить свойства функции.