Формулы сокращённого умножения

Формулы сокращённого умножения 7 класс

У математиков существует

свой язык - это формулы.

С. Ковалевская.

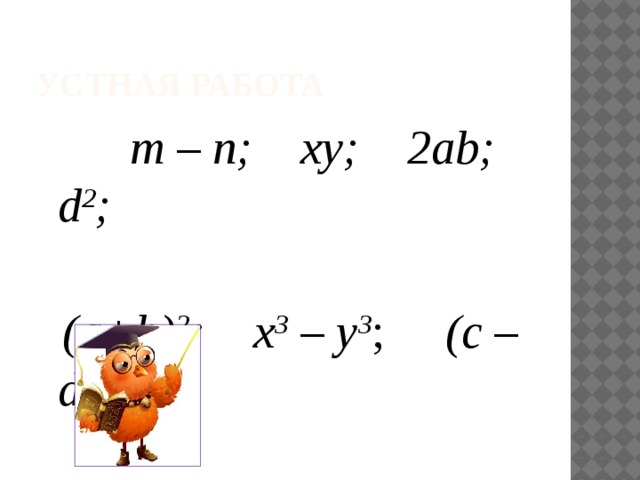
Устная работа

m – n; xy; 2ab; d 2 ;

(a+b) 2 ; x 3 – y 3 ; (c – d) 3

Математический диктант

I.

• Найдите квадраты выражений: 4х ; 5у ;
• Найдите произведение: 4х и 5у ;
• Найдите удвоенное произведение:

4х и 5у ;

• Найдите произведение многочленов

( 4 – у ) и ( 5 + х) ;

Математический диктант

• Запишите на математическом языке:

• Квадрат разности чисел m и 3 ;
• Разность квадратов чисел y и 6;
• Сумма кубов чисел b и 1 .

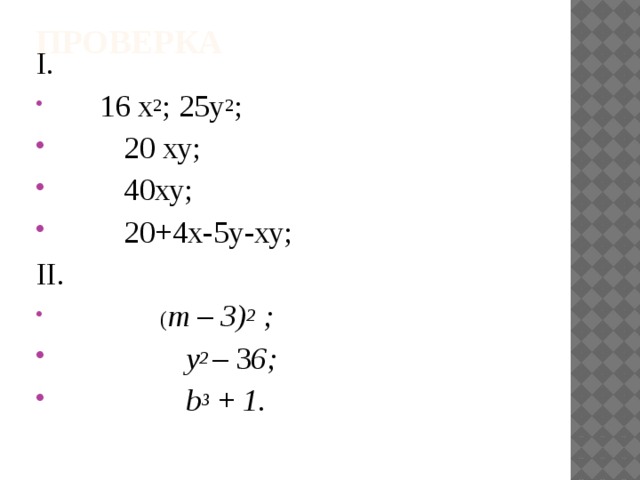
Проверка

I.

• 16 х 2 ; 25у 2 ; 
• 20 ху; 
• 40ху; 
• 20+4х-5у-ху;

II.

• ( m – 3) 2 ;
• y 2 – 3 6;
• b 3 + 1 .

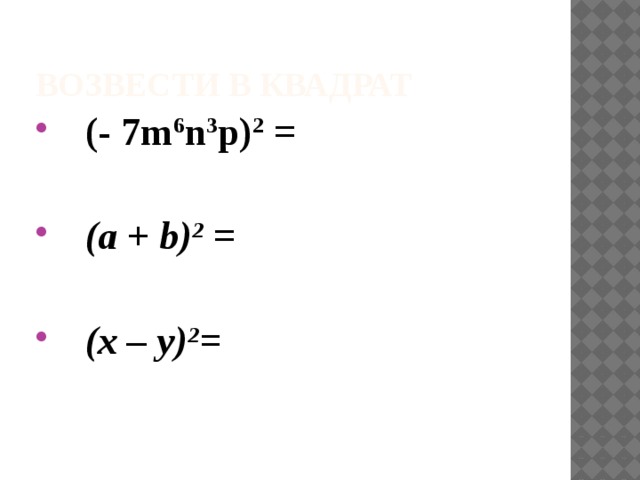
Возвести в квадрат

• (- 7m 6 n 3 p) 2 =

• (a + b) 2 =

• (х – у) 2 =

Цель урока:

Вывести новые формулы

(a + b) 2

(a - b) 2

Квадрат суммы и квадрат разности.

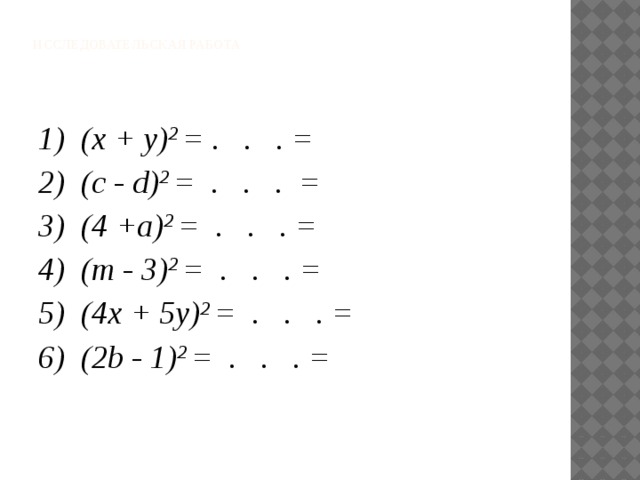
Исследовательская работа

1) (x + y) 2 = . . . =

2) (c - d) 2 = . . . =

3) (4 +a) 2 = . . . =

4) (m - 3) 2 = . . . =

5) (4x + 5у) 2 = . . . =

6) (2b - 1) 2 = . . . =

Вывод:

(a + b) 2 = … + … + …

Квадрат суммы двух выражений равен

. . . . . . плюс их . .

( a - b) 2 = … - … +

Квадрат разности двух выражений равен . . . . . . минус их

сумме их квадратов

удвоенное произведение

сумме их квадратов

удвоенное произведение

(

(

Квадрат разности

2

2

(

2

-

2

-

+

=

Квадрат суммы

2

2

(

2

2

+

+

+

=

Зарядка для глаз

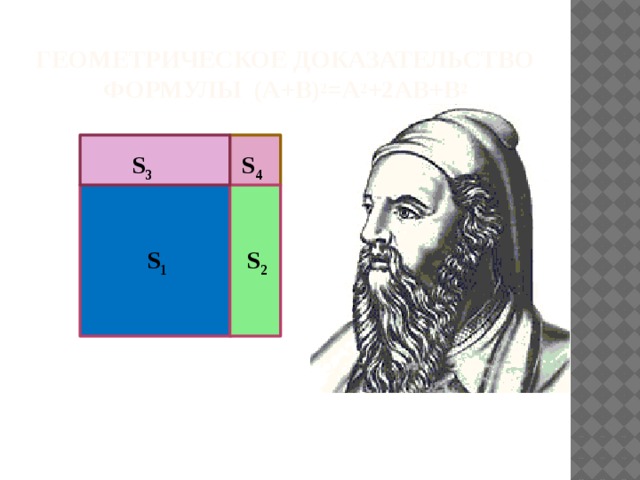
Геометрическое доказательство формулы (a+b) 2 =a 2 +2ab+b 2

S 4

S 3

S 1

S 2

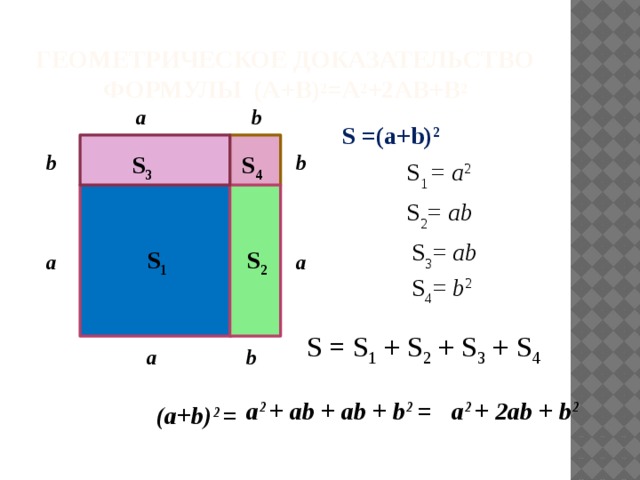
Геометрическое доказательство формулы (a+b) 2 =a 2 +2ab+b 2

a

b

S =(a+b) 2

b

S 3

b

S 4

S 1 = a 2

S 2 = ab

S 3 = ab

S 2

S 1

a

a

S 4 = b 2

S = S 1 + S 2 + S 3 + S 4

a

b

a 2 + ab + ab + b 2 =

a 2 + 2ab + b 2

(a+b) 2 =

Закрепление

№ 28.6

№ 28.2 (устно)

№ 28.4 (устно)

Самостоятельная работа (тест)

задания

1

(t – m) 2

2

(b +9) 2

t 2 –m 2

3

(7a – 1) 2

t 2 +m 2

b 2 +9b+81

(2x +3y) 2

t 2 -2tm+m 2

49a 2 -14a+2

b 2 +18b+81

49a 2 -14a-1

b 2 +81

4x 2 +12xy+9y

49a 2 -14a+1

4x 2 +6xy+9y 2

4x 2 +12xy+9y 2

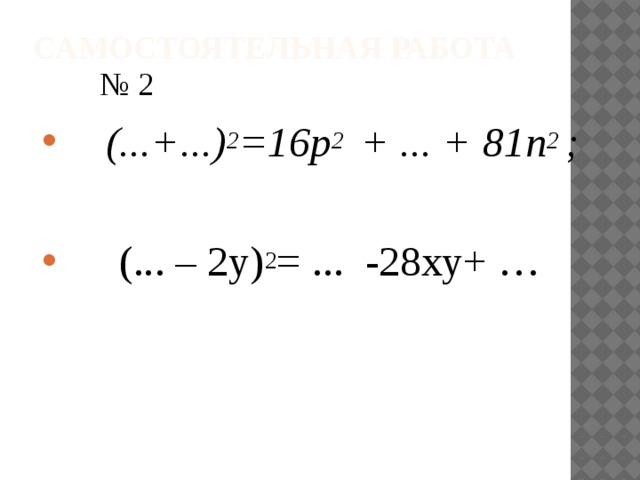
Самостоятельная работа

№ 2

• (...+...) 2 =16p 2 + ... + 81n 2 ;

• (... – 2y) 2 = ... -28ху+ …

Самопроверка

№ 1.

3233.

№ 2.

а) (4p + 9n) 2 = 16p 2 + 72pn + 81n 2 ;

б) (7 - 2y) 2 = 49 - 28xy + 4y 2 .

Быстрый счёт

(

А я догадался, как можно использовать эти формулы для быстрых вычислений.

91 2 =

32 2 =

58 2 =

2

2

2

(

2

_

_

+

+

+

=

Итог урока

Рефлексия деятельности (да, нет)

• Я знаю формулы сокращенного умножения: квадрат суммы и квадрат разности;
• Я научился применять эти формулы при упрощении выражений;
• Я знаю, как применять формулы при упрощении выражений, но в самостоятельной работе у меня были ошибки
• Данная тема не вызвала у меня затруднений

Домашнее задание

• п.28, № 28.3, 28.5, 28.14(б, в), 28.16(б, в),

28.58 * ;

• *придумать примеры на применение

формул квадрата суммы и квадрата

разности