Формулы приведения

Синус, косинус суммы и разности аргументов (урок-закрепление)

Сначала вспомним формулы для синуса и косинуса суммы и разности

• Sin (x+y) = sinxcosy + cosxsiny
• Sin (x-y) = sinxcosy – cosxsiny
• cos (x+y) = cosxcosy – sinxsiny
• cos (x-y) = cosxcosy + sinxsiny

формул всего 4

Как быстро их запомнить? формул всего 4

• Sin (x+y) = sinxcosy + cosxsiny
• Sin (x-y) = sinxcosy – cosxsiny
• cos (x+y) = cosxcosy – sinxsiny
• cos (x-y) = cosxcosy + sinxsiny

Для функции синуса сумма произведений смешанные, а для функции косинуса – сумма произведений одноименных функций

Эти формулы можно использовать для вывода формул приведения

• Sin( х) = sincosх cossinх= = 1cosх 0sinх = cosх
• cos(х) = coscosх + sinsinх=

= 0 cosх + 1sinх = sinх

Но это очень трудоемкая работа, каждый раз вычислять по формулам, но и запомнить трудновато – всего формул у нас будет 16! Это еще не считая формул приведения для тангенса и котангенса!

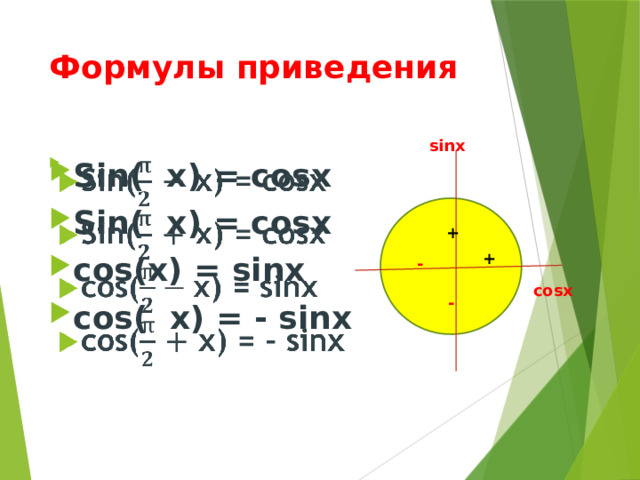
Формулы приведения

sinх

• Sin( х) = cosх
• Sin( х) = cosx
• cos(х) = sinx
• cos( х) = - sinx

+

+

-

cosх

-

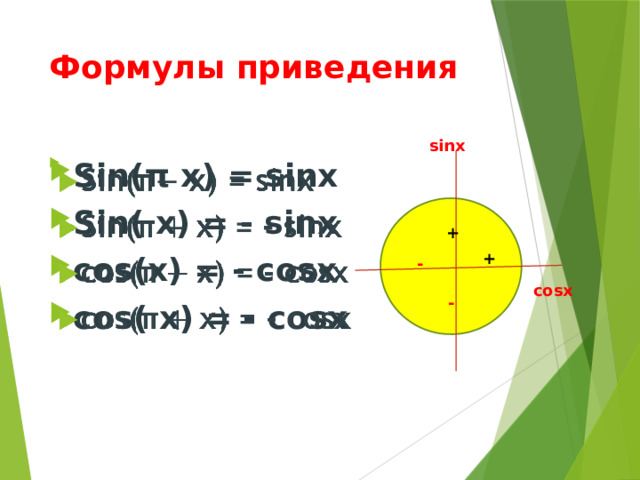
Формулы приведения

sinх

• Sin(π х) = sinх
• Sin( х) = - sinx
• cos(х) = - cosx
• cos( х) = - cosx

+

+

-

cosх

-

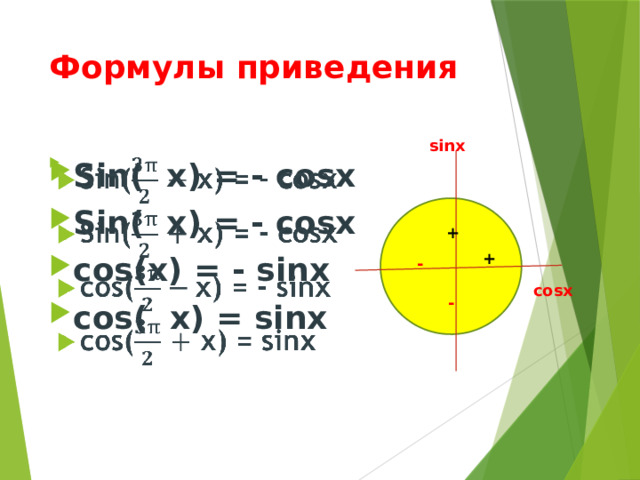
Формулы приведения

sinх

• Sin( х) = - cosх
• Sin( х) = - cosx
• cos(х) = - sinx
• cos( х) = sinx

+

+

-

cosх

-

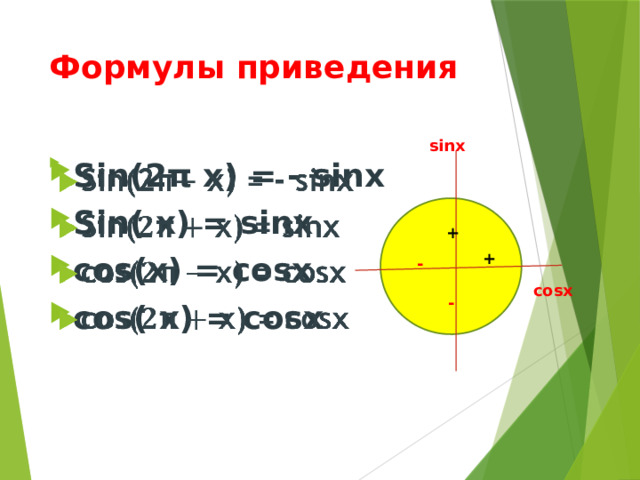
Формулы приведения

sinх

• Sin(2π х) = - sinх
• Sin( х) = sinx
• cos(х) = cosx
• cos( х) = cosx

+

+

-

cosх

-

Эти формулы легко запомнить , достаточно нарисовать единичную окружность и на ней нанести знаки полуосей. Заметьте, что для формул, содержащих и (дробные числа), название функции меняется! А для формул, содержащих целые числа 2π и π , название функции не меняется! cos( х) = - sinx Sin( х) = - sinx cos(х) = cosx Sin( х) = - cosx

sinх

А теперь разберемся со знаками перед полученными функциями.

1. Определяем в какой четверти лежит данный угол. Например: х – угол 2 четверти х – угол 3 четверти, х – угол 4 четверти и т.д.

+

cosх

+

-

-

2. Перед функцией ставим тот знак, который принимает функция в данной четверти. Например, cos( х) = - sinx, т.к. х – угол 2 четверти , и здесь функция cosх принимает – знак cos(х) = cosx, т.к. х – угол 4 четверти , и здесь функция cosх принимает + знак.

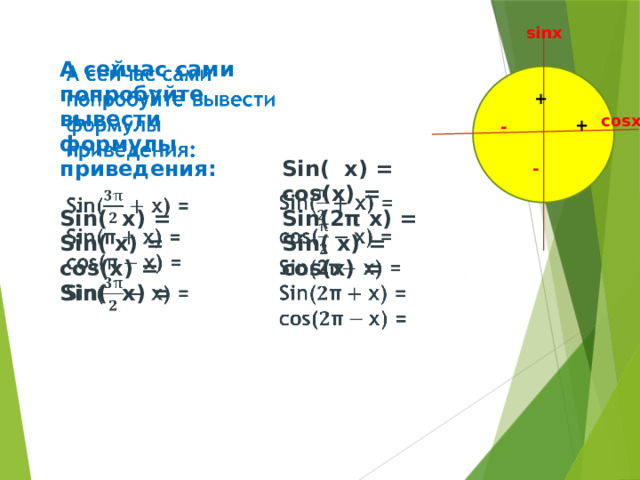
sinх

А сейчас сами попробуйте вывести формулы приведения:

Sin( х) =

Sin( х) =

cos(х) =

Sin( х) =

Sin( х) =

cos(х) =

Sin(2π х) =

Sin( х) =

cos(х) =

+

cosх

+

-

-

Спасибо за работу!