"Физика в задачах" 7-9 класс

Аннотация

В качестве школьного предмета физика вносит основной вклад в формирование естественнонаучной картины мира школьников и предоставляет наиболее ясные образцы применения научного метода познания, то есть способа получения достоверных знаний об окружающем мире. Задачи школьного физического образования состоят не только в выявлении и подготовке талантливых молодых людей для продолжения образования и дальнейшей профессиональной деятельности в области естественнонаучных исследований и создании новых технологий. Не менее важным является формирование естественнонаучной грамотности и интереса к науке у основной массы учащихся, которые в дальнейшем будут заняты в самых разнообразных сферах деятельности.

В основе курса разнообразные расчетные, качественные и текстовые задачи на физические явления и законы, которые могут провести под руководством учителя обучающиеся 13-15 лет.

Программа может быть реализована учителями физики как факультативный курс в 7-9 классах ОУ при реализации ФГОС ООО.

СОДЕРЖАНИЕ

1. Пояснительная записка 3

2. Планируемые результаты освоения программы «Физика в задачах» 4

3. Содержание программы 6

4. Тематическое планирование 20

5. Приложения……………………………………………………………………….........24

1. Пояснительная записка

Программа факультативного курса по направлению общеинтеллектуальное развитие личности «Физика в задачах» для 7-9 классов является авторской программой, рассчитана на 102 часа (3 года по 1 часу в неделю) и разработана в соответствии с нормативными документами:

- Федеральный закон от 29.12.2012 N 273-ФЗ "Об образовании в Российской Федерации";

- Приказ Министерства образования Российской Федерации от 17 декабря 2010 № 1897 «Об утверждении ФГОС ООО»;

- Постановление Главного государственного санитарного врача РФ от 29.12.2010 №189 «Об утверждении СанПин 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях»;

- Основная образовательная программа основного общего образования муниципального бюджетного образовательного учреждения «Гимназия №1» г. Ангарска;

Программа развития гимназии «Школа социального опыта» (2017-2022 гг.).

Актуальность

В изучении курса физики решение задач имеет исключительно большое значение и им должно отводиться значительная часть курса. Решение и анализ задач позволяет понять и запомнить основные законы и формулы физики, создаёт представление об их характерных особенностях и границах применения. Задачи развивают навык в использовании общих законов материального мира для решения конкретных вопросов, имеющих практическое и познавательное значение. А в условиях, когда усиливается роль самостоятельности и активности в обучении и развитии мышления, умение решать задачи является лучшим критерием оценки глубины изучения программного материала и его усвоения. Огромную роль в качественном усвоении физики играет решение не только расчётных, но и качественных графических, текстовых задач, задач с использованием рисунков и таблиц. Качественные задачи заставляют анализировать физическую сущность явления, строить гипотезы и их обоснование, а соответственно способствуют развитию логического и образного мышления, а также учат строить правильные формулировки с точки зрения языка. В расчётных задачах реализуется математический язык, логика, прослеживаются наглядно зависимости величин.

Количество нового материала в учебниках 7-9 классах не помещается в 68 часов и поэтому не остается времени на повторение. Знания получаются поверхностные. В упражнениях учебников после теории нет задач, которые встречаются на ГИА. Уровень изучения механики в 9 классе (снижен) не соответствует уровню заданий проверяемых на ОГЭ. Например, на изучение темы «Движение тела под действием нескольких сил» отведено всего 2 урока, при этом не повторяются и не изучаются сила упругости, трения, а в ОГЭ включено задание на динамику с развернутым ответом.

Данный курс «Физика в задачах» поддерживает изучение основного курса физики и способствует лучшему усвоению его базового курса. Материал данного курса уделяет большее внимание тем вопросам программы, которые вызывают особый интерес школьников, имеют наибольшую ценность в решении задач профориентации учащихся. Познавательный материал курса будет способствовать не только выработке умений и закреплению навыков, но и формированию устойчивого интереса учащихся к процессу и содержанию деятельности, а также познавательной и социальной активности. Наряду с основной задачей расширения и углубления теоретического и практического изучения школьного курса физики данный курс позволяет ближе подвести учащихся к современному уровню развития науки, что обеспечит больший интерес к предмету.

Образовательная деятельность и учебное сотрудничество в ходе изучения курса служит достижению целей личностного и социального развития обучающихся.

Курс знакомит учащихся с многочисленными явлениями физики через решение задач различного типа. Логика подачи материала в программе выстроена от наблюдения и анализа окружающих явлений к выводам и знаниям, помогающим их объяснить с научной точки зрения.

Новизна.

Новизна факультативного курса «Физика в задачах» заключается в непрерывности и последовательности углублённого изучения учебного материала, в преемственности изучения разделов курса физики с опорой на изученное в предыдущие годы. Она позволяет решать задачи на качественно новом уровне.

Курс знакомит с интересными качественными и расчетными задачами творческого характера, задачами с использованием графиков и рисунков, что будет формировать интерес к физике и развивать любознательность.

Методологическая основа программы базируется на личностно-ориентированном подходе с учётом возрастных особенностей обучающихся 13-15 лет.

Цель: создание условий для развития, саморазвития творческих способностей учащихся, их интересов и подготовки к продолжению образования с учетом личностного потенциала каждого учащегося, приучение к научному познанию мира, развитие у обучающихся интереса к изучению физики и подготовка их к углублённому изучению курса физики.

Задачи образовательные: способствовать созданию условий для формирования первоначальных представлений о физической сущности явлений природы (механических, тепловых, электромагнитных), ознакомить обучающихся с простейшими механизмами и увлекательно-познавательными опытами, в основе которых лежат физические законы; раскрыть закономерности наблюдаемых явлений, их практическое применение.

Задачи развивающие: развитие общеучебных мыслительных умений и навыков для решения задач творческого и исследовательского характера; потребности и умения самостоятельно приобретать и пополнять свои знания; совершенствование полученных знаний в основном курсе знаний и умение применять их в конкретных, проблемных ситуациях; активизация познавательного интереса к физике и технике, профессиональное самоопределение.

 Задачи воспитательные: способствовать формированию уважительного и доброжелательного отношения к другому человеку, его мнению; развивать мотивацию к обучению и целенаправленной познавательной деятельности.

Межпредметные связи программы факультативного курса

Программа факультативного курса «Физика в задачах» носит комплексный характер, что отражено в межпредметных связях, с такими учебными дисциплинами, как астрономия, математика.

2. Планируемые результаты освоения программы «Физика в задачах»

В процессе обучения у обучающихся формируются познавательные, личностные, регулятивные, коммуникативные универсальные учебные действия.

Личностными результатами программы факультативного курса является формирование следующих компетенций:

• сформированность познавательных интересов, интеллектуальных и творческих способностей учащихся;

• убежденность в возможности познания природы, в необходимости разумного использования достижений науки и технологий для дальнейшего развития человеческого общества, уважение к творцам науки и техники, отношение к физике как элементу общечеловеческой культуры;

• самостоятельность в приобретении новых знаний и практических умений;

• готовность к выбору жизненного пути в соответствии с собственными интересами и возможностями;

• мотивация образовательной деятельности школьников на основе личностно ориентированного подхода;

• формирование ценностных отношений друг к другу, учителю, авторам открытий и изобретений, результатам обучения.

Метапредметными результатами программы факультативного курса является формирование следующих универсальных учебных действий (УУД):

Регулятивные УУД:

• Определять и формулировать цель деятельности.

• Ставить учебную задачу.

• Учиться составлять план и определять последовательность действий.

• Учиться работать по предложенному плану.

• Учиться самостоятельно формулировать проблему и пути поиска решения.

• Учиться отличать верно выполненное задание от неверного.

• Учиться совместно с учителем и другими учениками давать эмоциональную оценку деятельности

Познавательные УУД:

• Добывать новые знания: находить ответы на вопросы, используя схемы-опоры, ПК, учебный текст, свой жизненный опыт и информацию, полученную на занятиях.

• Перерабатывать полученную информацию: делать выводы в результате совместной работы всей группы.

• Преобразовывать информацию из одной формы в другую: составлять рассказы на основе простейших моделей (предметных, рисунков, схематических рисунков, схем); находить и формулировать решение задачи с помощью простейших моделей (предметных, рисунков, схематических рисунков).

Коммуникативные УУД:

• Уметь донести свою позицию до других: оформлять свою мысль в устной и письменной речи (на уровне одного предложения или небольшого текста).

• Слушать и понимать речь других.

• Совместно договариваться о правилах общения и поведения в школе и следовать им.

• Учиться выполнять различные роли в группе (лидера, исполнителя, критика).

При изучении курса «Физика в задачах» в соответствии с требованиями ФГОС ООО формируются следующие предметные результаты:

• приобретение учащимися знаний о дискретном строении вещества, механических, тепловых, электромагнитных и квантовых явлениях;

• описание и объяснение явлений с использованием полученных знаний, требующих создания и использования физических моделей, творческих и практико-ориентированных задач;

• освоение приемов работа с информацией физического содержания, включая информацию о современных достижениях физики; анализ и критическое оценивание информации;

• знакомство учащихся со сферами профессиональной деятельности, связанными с физикой, и современными технологиями, основанными на достижениях физической науки.

Содержание программы

№	Раздел программы	Количество часов	Характеристика основных видов деятельности учащихся	Формы организации занятий
7 класс
1	Физическая задача. Классификация задач	1	- знать правила оформления задач	индивидуальная работа; фронтальная работа; групповая форма работы.
2	Правила и примы решения физических задач	2	- понимать физические термины: тело, вещество, материя; - уметь проводить наблюдения физических явлений; - измерять физические величины: расстояние, промежуток времени, температуру; - определять цену деления шкалы при­бора с учетом погрешности измерения.	индивидуальная работа; фронтальная работа; групповая форма работы.
3	Первоначальные сведения о строении вещества	3	- распознавать тепловые явления и объяснять на базе имеющихся знаний основные свойства или условия протекания этих явлений: диффузия, изменение объема тел при нагревании (охлаждении), большая сжимаемость газов, малая сжимаемость жидкостей и твердых тел; агрегатные состояния вещества, - описывать изученные свойства тел и тепловые явления, используя физические величины; - при описании правильно трактовать физический смысл используемых величин, их обозначения и единицы измерения, находить формулы, связывающие данную физическую величину с другими величинами, вычислять значение физической величины; -анализировать свойства тел, тепловые явления и процессы, используя основные положения атомно-молекулярного учения о строении вещества; - различать основные признаки изученных физических моделей строения газов, жидкостей и твердых тел.	индивидуальная работа; фронтальная работа; групповая форма работы. работа по карточкам; работа с картой; работа у доски; заполнение таблиц; работа с учебниками и т. д. беседа; обсуждение; сравнение.
4	Взаимодействие тел	12	- распознавать механические явления и объяснять на основе имеющихся знаний основные свойства или условия протекания этих явлений: равномерное и неравномерное движение, инерция, взаимодействие тел, - описывать изученные свойства тел и механические явления, используя физические величины: путь, скорость, сила (сила тяжести, сила упругости, сила трения), - правильно трактовать физический смысл используемых величин, их обозначения и единицы измерения, находить формулы, связывающие данную физическую величину с другими величинами, вычислять значение физической величины; анализировать свойства тел, механические явления и процессы, используя физические законы: принцип суперпозиции сил (нахождение равнодействующей силы), - при этом различать словесную формулировку закона и его математическое выражение; - различать основные признаки изученных физических моделей: материальная точка, система отсчета; решать задачи, используя физические законы и формулы, связывающие физические величины (путь, скорость, сила, сила трения скольжения), на основе анализа условия задачи записывать краткое условие, выделять физические величины, законы и формулы, необходимые для ее решения, проводить расчеты и оценивать реальность полученного значения физической величины.	индивидуальная работа; фронтальная работа; групповая форма работы
5	Давление твердых тел, жидкостей и газов	10	- распознавать механические явления и объяснять на основе имеющихся знаний основные свойства или условия протекания этих явлений: передача давления твердыми телами, жидкостями и газами, атмосферное давление, плавание тел; - описывать изученные свойства тел и механические явления, используя физические величины: давление; - при описании правильно трактовать физический смысл используемых величин, их обозначения и единицы измерения, находить формулы, связывающие данную физическую величину с другими величинами, вычислять значение физической величины; - анализировать свойства тел, механические явления и процессы, используя физические законы: закон Паскаля, закон Архимеда; - при этом различать словесную формулировку закона и его математическое выражение; - решать задачи, используя физические законы (закон Паскаля, закон Архимеда) и формулы, связывающие физические величины (давление): на основе анализа условия задачи записывать краткое условие, выделять физические величины, законы и формулы, необходимые для ее решения, проводить расчеты и оценивать реальность полученного значения физической величины	индивидуальная работа; фронтальная работа; групповая форма работы
6	Работа и мощность. Энергия	7	- описывать изученные свойства тел и механические явления, используя физические величины: механическая работа, механическая мощность, КПД при совершении работы с использованием простого механизма; - при описании правильно трактовать физический смысл используемых величин, их обозначения и единицы измерения, находить формулы, связывающие данную физическую величину с другими величинами, вычислять значение физической величины; - решать задачи, используя физические формулы, связывающие физические величины (механическая работа, механическая мощность, КПД простого механизма): на основе анализа условия задачи записывать краткое условие, выделять физические величины, законы и формулы, необходимые для ее решения, проводить расчеты и оценивать реальность полученного значения физической величины	индивидуальная работа; фронтальная работа; групповая форма работы. работа по карточкам; работа с картой; работа у доски; заполнение таблиц; работа с учебниками и т. д.  беседа; обсуждение; сравнение.
8 класс
7	Тепловые явления	11	- распознавать тепловые явления и объяснять на базе имеющихся знаний основные свойства или условия протекания этих явлений: диффузия, изменение объема тел при нагревании (охлаждении), большая сжимаемость газов, малая сжимаемость жидкостей и твердых тел; тепловое равновесие, испарение, конденсация, плавление, кристаллизация, кипение, влажность воздуха, различные способы теплопередачи (теплопроводность, конвекция, излучение), агрегатные состояния вещества, поглощение энергии при испарении жидкости и выделение ее при конденсации пара, зависимость температуры кипения от давления; - описывать изученные свойства тел и тепловые явления, используя физические величины: количество теплоты, внутренняя энергия, температура, удельная теплоемкость вещества, удельная теплота плавления, удельная теплота парообразования, удельная теплота сгорания топлива, коэффициент полезного действия теплового двигателя; - при описании правильно трактовать физический смысл используемых величин, их обозначения и единицы измерения, находить формулы, связывающие данную физическую величину с другими величинами, вычислять значение физической величины; анализировать свойства тел, тепловые явления и процессы, используя основные положения атомно-молекулярного учения о строении вещества и закон сохранения энергии; - различать основные признаки изученных физических моделей строения газов, жидкостей и твердых тел; - приводить примеры практического использования физических знаний о тепловых явлениях; - решать задачи, используя закон сохранения энергии в тепловых процессах и формулы, связывающие физические величины (количество теплоты, температура, удельная теплоемкость вещества, удельная теплота плавления, удельная теплота парообразования, удельная теплота сгорания топлива, коэффициент полезного действия теплового двигателя): на основе анализа условия задачи записывать краткое условие, выделять физические величины, законы и формулы, необходимые для ее решения, проводить расчеты и оценивать реальность полученного значения физической величины.	индивидуальная работа; фронтальная работа; групповая форма работы. работа по карточкам; работа с картой; работа у доски; заполнение таблиц; работа с учебниками и т. д.  беседа; обсуждение; сравнение.
8	Электрические явления	12	- распознавать электрические явления и объяснять на основе имеющихся знаний основные свойства или условия протекания этих явлений: электризация тел, взаимодействие зарядов, электрический ток и его действия (тепловое, химическое, магнитное), - составлять схемы электрических цепей с последовательным и параллельным соединением элементов, различая условные обозначения элементов электрических цепей (источник тока, ключ, резистор, реостат, лампочка, амперметр, вольтметр). - описывать изученные свойства тел и электромагнитные явления, используя физические величины: электрический заряд, сила тока, электрическое напряжение, электрическое сопротивление, удельное сопротивление вещества, работа электрического поля, мощность тока, - при описании верно трактовать физический смысл используемых величин, их обозначения и единицы измерения; - находить формулы, связывающие данную физическую величину с другими величинами. анализировать свойства тел, электрические явления и процессы, используя физические законы: закон сохранения электрического заряда, закон Ома для участка цепи, закон Джоуля-Ленца; - при этом различать словесную формулировку закона и его математическое выражение. - приводить примеры практического использования физических знаний о электромагнитных явлениях; - решать задачи, используя физические законы (закон Ома для участка цепи, закон Джоуля-Ленца,) и формулы, связывающие физические величины (сила тока, электрическое напряжение, электрическое сопротивление, удельное сопротивление вещества, работа электрического поля, мощность тока, формулы расчета электрического сопротивления при последовательном и параллельном соединении проводников): - на основе анализа условия задачи записывать краткое условие, выделять физические величины, законы и формулы, необходимые для ее решения, проводить расчеты и оценивать реальность полученного значения физической величины.	индивидуальная работа; фронтальная работа; групповая форма работы. работа по карточкам; работа с картой; работа у доски; заполнение таблиц; работа с учебниками и т. д.  беседа; обсуждение; сравнение.
9	Электромагнитные явления	4	- распознавать электромагнитные явления и объяснять на основе имеющихся знаний основные свойства или условия протекания этих явлений: взаимодействие магнитов, электромагнитная индукция, действие магнитного поля на проводник с током - описывать изученные свойства тел и электромагнитные явления - при описании верно трактовать физический смысл используемых величин, их обозначения и единицы измерения; находить формулы, связывающие данную физическую величину с другими величинами. - анализировать свойства тел, электромагнитные явления - приводить примеры практического использования физических знаний о электромагнитных явлениях	индивидуальная работа; фронтальная работа; групповая форма работы. работа по карточкам; работа с картой; работа у доски; заполнение таблиц; работа с учебниками и т. д.  беседа; обсуждение; сравнение.
10	Световые явления	8	- распознавать световые явления и объяснять на основе имеющихся знаний основные свойства или условия протекания этих явлений: прямолинейное распространение света, отражение и преломление света, - использовать оптические схемы для построения изображений в плоском зеркале и собирающей линзе. - описывать изученные свойства тел и световые явления, используя физические величины: фокусное расстояние и оптическая сила линзы; - находить формулы, связывающие данную физическую величину с другими величинами. - анализировать свойства тел, световые явления и процессы, используя физические законы: закон прямолинейного распространения света, закон отражения света, закон преломления света; - при этом различать словесную формулировку закона и его математическое выражение. - приводить примеры практического использования физических знаний о световых явлениях решать задачи, используя физические законы (закон прямолинейного распространения света, закон отражения света, закон преломления света) и формулы, связывающие физические величины (фокусное расстояние и оптическая сила линзы): -на основе анализа условия задачи записывать краткое условие, выделять физические величины, законы и формулы, необходимые для ее решения, проводить расчеты и оценивать реальность полученного значения физической величины.	индивидуальная работа; фронтальная работа; групповая форма работы. работа по карточкам; работа с картой; работа у доски; заполнение таблиц; работа с учебниками и т. д.  беседа; обсуждение; сравнение.
9 класс
11	Законы взаимодействия и движения тел	15	- распознавать механические явления и объяснять на основе имеющихся знаний основные свойства или условия протекания этих явлений: равномерное и равноускоренное прямолинейное движение, относительность механического движения, свободное падение тел, равномерное движение по окружности, инерция, взаимодействие тел, реактивное движение; -описывать изученные свойства тел и механические явления, используя физические величины: путь, перемещение, скорость, ускорение, период обращения, масса тела, сила (сила тяжести, сила упругости, сила трения), импульс тела, кинетическая энергия, потенциальная энергия, механическая работа, механическая мощность; - при описании правильно трактовать физический смысл используемых величин, их обозначения и единицы измерения, находить формулы, связывающие данную физическую величину с другими величинами, вычислять значение физической величины; анализировать свойства тел, механические явления и процессы, используя физические законы: закон сохранения энергии, закон всемирного тяготения, принцип суперпозиции сил (нахождение равнодействующей силы), I, II и III законы Ньютона, закон сохранения импульса; при этом различать словесную формулировку закона и его математическое выражение; - различать основные признаки изученных физических моделей: материальная точка, инерциальная система отсчета; - решать задачи, используя физические законы (закон сохранения энергии, закон всемирного тяготения, принцип суперпозиции сил, I, II и III законы Ньютона, закон сохранения импульса) и формулы, связывающие физические величины (путь, скорость, ускорение, масса тела, импульс тела, кинетическая энергия, потенциальная энергия, механическая работа, механическая мощность): на основе анализа условия задачи записывать краткое условие, выделять физические величины, законы и формулы, необходимые для ее решения, проводить расчеты и оценивать реальность полученного значения физической величины	индивидуальная работа; фронтальная работа; групповая форма работы. работа по карточкам; работа с картой; работа у доски; заполнение таблиц; работа с учебниками и т. д.  беседа; обсуждение; сравнение.
12	Механические колебания и волны. Звук	5	- распознавать механические явления и объяснять на основе имеющихся знаний основные свойства или условия протекания этих явлений: колебательное движение, резонанс, волновое движение (звук); описывать изученные свойства тел и механические явления, используя физические величины: период обращения, амплитуда, период и частота колебаний, длина волны и скорость ее распространения; - при описании правильно трактовать физический смысл используемых величин, их обозначения и единицы измерения, находить формулы, связывающие данную физическую величину с другими величинами, вычислять значение физической величины; - различать основные признаки изученных физических моделей; - решать задачи, используя физические законы и формулы, связывающие физические величины (амплитуда, период и частота колебаний, длина волны и скорость ее распространения): на основе анализа условия задачи записывать краткое условие, выделять физические величины, законы и формулы, необходимые для ее решения, проводить расчеты и оценивать реальность полученного значения физической величины	индивидуальная работа; фронтальная работа; групповая форма работы. работа по карточкам; работа с картой; работа у доски; заполнение таблиц; работа с учебниками и т. д.  беседа; обсуждение; сравнение.
13	Электромагнитное поле	10	- распознавать электромагнитные явления и объяснять на основе имеющихся знаний основные свойства или условия протекания этих явлений: взаимодействие магнитов, электромагнитная индукция, действие магнитного поля на проводник с током и на движущуюся заряженную частицу, действие электрического поля на заряженную частицу, электромагнитные волны, преломление света, дисперсия света. - описывать изученные свойства тел и электромагнитные явления, используя физические величины: скорость электромагнитных волн, длина волны и частота света; - при описании верно трактовать физический смысл используемых величин, их обозначения и единицы измерения; находить формулы, связывающие данную физическую величину с другими величинами; - анализировать свойства тел, электромагнитные явления и процессы, используя физические законы: закон преломления света; при этом различать словесную формулировку закона и его математическое выражение; - приводить примеры практического использования физических знаний о электромагнитных явлениях решать задачи, используя физические законы (закон преломления света) и формулы, связывающие физические величины (скорость электромагнитных волн, длина волны и частота света,); - на основе анализа условия задачи записывать краткое условие, выделять физические величины, законы и формулы, необходимые для ее решения, проводить расчеты и оценивать реальность полученного значения физической величины.	индивидуальная работа; фронтальная работа; групповая форма работы. работа по карточкам; работа с картой; работа у доски; заполнение таблиц; работа с учебниками и т. д.  беседа; обсуждение; сравнение.
14	Строение атома и атомного ядра	5	- распознавать квантовые явления и объяснять на основе имеющихся знаний основные свойства или условия протекания этих явлений: естественная и искусственная радиоактивность, α-, β- и γ-излучения, возникновение линейчатого спектра излучения атома; - описывать изученные квантовые явления, используя физические величины: массовое число, зарядовое число, период полураспада, энергия фотонов; - при описании правильно трактовать физический смысл используемых величин, их обозначения и единицы измерения; - находить формулы, связывающие данную физическую величину с другими величинами, вычислять значение физической величины; - анализировать квантовые явления, используя физические законы и постулаты: закон сохранения энергии, закон сохранения электрического заряда, закон сохранения массового числа, при этом различать словесную формулировку закона и его математическое выражение; - различать основные признаки планетарной модели атома, нуклонной модели атомного ядра; - приводить примеры проявления в природе и практического использования радиоактивности, ядерных и термоядерных реакций	индивидуальная работа; фронтальная работа; групповая форма работы. работа по карточкам; работа с картой; работа у доски; заполнение таблиц; работа с учебниками и т. д.  беседа; обсуждение; сравнение.
Итого 105

1. Тематическое планирование

№	Тема занятий	Содержание занятий
7 класс
	Физическая задача. Классификация задач	1. Состав физической за­дачи. Классификация физических задач.
	Правила и приемы решения задач	1.Общие требования при решении физических задач. Этапы решения задачи. 2. Виды физических приборов. Цена деления. Точность и погрешность измерений.
	Первоначальные сведения о строении вещества	1.Строение вещества. Основные положения МКТ строения вещества. 2.Взаимное притяжение и отталкивание молекул. Явления смачивания и несмачивания. 3.Агрегатные состояния вещества.
	Взаимодействия тел	1.Механическое движение. Относительность механического движения. (2 ч) 2. Прямолинейное равномерное движение и его характеристики: траектория, перемещение, путь. 3.Физический смысл скорости. Графическое представление движения и решение задач. 4. Графический и координатный способы решения задач. 5.Алгоритм решения задач на расчет средней скорости при неравномерном движении. 6.Инерция и инертность 7. Плотность вещества (2ч) 8.Сила. Сила тяжести. 9.Сила упругости, Закон Гука. Виды деформаций. Вес тела. Невесомость. 10.Сила трения. Равнодействующая сил.
	Давление твердых тел, жидкостей и газов	1.Давление твёрдых тел. 2. Давление газа и жидкости. Закон Паскаля 3. Расчёт давления жидкости на дно и стенки сосуда. 4.Сообщающиеся сосуды 5. Сообщающиеся сосуды 6.Атмосферное давление. 7.Гидравлический пресс. 8.Архимедова сила. 9. Архимедова сила. 10. Плавание тел. Плавание судов. Воздухоплавание.
	Работа и мощность. Энергия. Механизмы	1.Механическая работа и мощность. 2. Простые механизмы. Рычаг. Момент силы. 3.Блок. «Золотое правило» механики. 4.Коэффициент полезного действия механизма. 5.Энергия. Потенциаль­ная и кинетическая энергия. Полная механическая энергия. 6.Алгоритм решения задач на закон сохранения и превращение механической энергии. 7.Центр тяжести тела. Условия равновесия тел. Определение положения центра тяжести плоской фигуры
8 класс
	Тепловые явления	1.Тепловое движение. Тепловое равновесие. Темпера­тура. Внутренняя энергия. 2. Работа и теплопередача. Тепло­проводность. Конвекция. Излучение. 3.Количество теплоты. Удельная теплоемкость. 5.Расчет количества теплоты при теп­лообмене. Закон сохранения и превращения энергии в меха­нических и тепловых процессах. 6.Плавление и отвердевание кристаллических тел. 7.Удельная теплота плавления. 8.Испаре­ние и конденсация. Кипение. 9.Влажность воздуха. Удельная теплота парообразования. 10.Объяснение изменения агрегатно­го состояния вещества на основе молекулярно-кинетических представлений. 11.КПД тепловых машин.
	Электрические явления	1.Электризация тел. Два рода электрических зарядов. Взаимодействие заряженных тел. 2.Проводники, диэлектри­ки и полупроводники. Закон сохране­ния электрического заряда. 3.Делимость электрического заря­да. Электрон. Строение атома. 4.Электрический ток. Действие электрического поля на электрические заряды. 5.Источники тока. Электрическая цепь. 6.Сила тока. Электрическое напря­жение. Электрическое сопротивление. 7.Закон Ома для участ­ка цепи. 8.Последовательное соединение про­водников. 9. Параллельное соединение про­водников. 10. Смешанное соединение проводников. 11.Работа и мощность электрического тока. Закон Джоуля—Ленца. 12.Конденсатор.
	Магнитные явления	1.Опыт Эрстеда. Магнитное поле. Магнитное поле пря­мого тока. 2. Магнитное поле катушки с током. Постоянные магниты. 3.Взаимодействие магнитов. 4.Действие магнитно­го поля на проводник с током.
	Световые явления	1.Источники света. Прямолинейное распространение света. 2.Отражение света. Закон отражения света. 3.Плоское зеркало. 4.Преломление света. За­кон преломления света. 5.Линзы. Фокусное расстояние лин­зы. Оптическая сила линзы. 6.Изображения, даваемые лин­зой. 7.Система линз 8.Построение изображений в линзах.
9 класс
1.	Законы взаимодействия и движения тел	Материальная точка. Система отсчета. Перемеще­ние. 1.Скорость прямолинейного равномерного движения. 2. Графики зависимости кинематических величин от времени при равномерном движении. 3.Прямолинейное равноускоренное движение: мгновенная скорость, ускорение, перемещение. 4.Графики зависимости кинематических величин от времени при равноускоренном движении. 5.Относительность механическо­го движения. 6.Инерциальная система отсчета. 7. Законы Ньютона. 8.Свободное падение. 9.Невесомость. Закон всемирного тяготе­ния. 10. Силы в механике. 11.Движение тала под действием нескольких сил. 12.Движение тала под действием нескольких сил. 13.Импульс. Закон со­хранения импульса. 14. Механическая работа и мощность 15. Потенциальная и кинетическая энергия. Закон сохранения энергии.
2.	Механические колебания и волны. Звук	1.Колебательное движение. Амплитуда, период, частота колебаний. Свободные колебания. 2.Колебания груза на пру­жине. 3.Математический маят­ник 4. Распространение колебаний в упругих сре­дах. Длина волны. 5.Звуковые волны. Скорость звука. Высота, тембр и громкость звука.
3.	Электромагнитное поле	1.Однородное и неоднородное магнитное поле. Направ­ление тока и направление линий его магнитного поля. 2.Пра­вило буравчика. Обнаружение магнитного поля. 3.Правило ле­вой руки. Индукция магнитного поля. 4.Магнитный поток. Опыты Фарадея. 5.Электромагнитная индукция. Направление индукционного тока. Правило Ленца. 6.Электро­магнитное поле. Электромагнитные волны. Колебательный контур. 7.Электромагнитная природа света. Преломление света. Пока­затель преломления.
4.	Строение атома и атомного ядра	1.Радиоактивность. Альфа-, бета- и гамма-излучения. 2.Ядерная модель атома. Радиоактивные превраще­ния атомных ядер. Изотопы. 3.Правила смещения для альфа- и бета-распада при ядерных реакциях. 4.Энергия связи частиц в ядре. 5.Период полураспада. Закон радиоактивного распада.

Приложение 1

Занятие по теме «Давление газа и жидкости. Закон Паскаля»

1. Теория

1. Расчетные задачи:

Уровень А

5.1 Если стакан сдавливать ладонями за горлышко и дно, то на одной ладони появится отпечаток, а на другой - нет. Почему?

5.2 Является ли единицей измерения давления 1 мН/км²?

5.3 Расположите давления в порядке уменьшения: 6 кН/м2, 60 Н/см2, 600 Па, 60 кН/дм2, 60 Н/м².

5.4 Тело находится в состоянии покоя на горизонтальной плоскости. Определить давление тела на эту плоскость. Масса тела т = 700 г. Площадь основания тела S = 35 см².

5.5 Алюминиевый кубик с ребром 20 мм лежит на столе. Какое давление создает кубик?

5.6 Тело находится в состоянии покоя на горизонтальной плоскости. Давление тела на эту плоскость р = 2 кПа. Определить массу тела. Площадь основания тела S = 45 см2.

5.7 Какое давление на пол производит стол массой т = 20 кг, если площадь каждой из четырех ножек S = 5 см2? Влиянием атмосферного давления пренебречь.

5.8 Ветер создает давление всего лишь 80 Па. С какой силой ветер толкает вперед яхту с площадью паруса 60 м2?

5.9 Определите высоту столба керосина, который оказывает гидростатическое давление на дно сосуда равное 4 ·103 Па.

5.10 Найдите гидростатическое давление на дно сосуда цилиндрической формы с площадью основания 50 см2, в который налили 2 л воды.

5.11 В каком из сосудов сила давления жидкости на дно больше веса, а в каком – меньше?

5.12 С какой силой атмосферный воздух давит на бумажный лист, расположенный на горизонтальном столе? Размеры листа 16 × 20 см, атмосферное давление 1·105 Па.

5.13 Давление газа в баллоне 23 кПа. С какой силой газ давит на дно баллона площадью 3,2 дм2?

5.14 Высота столба ртути, уравновешивающего атмосферное давление, равна 760 мм. Во сколько раз будет больше высота столба воды, уравновешивающего это давление?

5.15 Во сколько раз высота столба жидкости в спиртовом барометре будет больше, чем в pтyтном барометре? Давление атмосферное. (ρртути = 13,6 г/см3 , ρспирта = 0,79 кг/дм3).

5.16 Водяной насос может создавать давление не более 220 кПа. На какую высоту он сможет подавать воду?

Уровень В

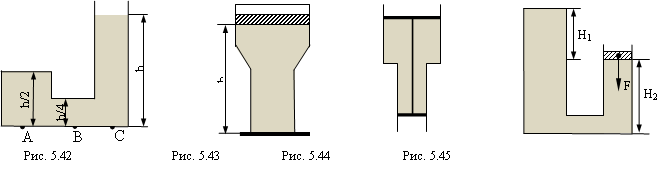
5.17 Какое наибольшее и наименьшее давления может создавать оловянный брусок с размерами 10×5×8 см?

5.18 Оловянный брусок с размерами 10 × 20 × 25 см и массой 5 кг лежит на столе своей большей гранью. Какое он создает давление?

5.19 Какая сторона бетонного блока с размерами 50 × 150 ×100 см опирается на землю, если блок создает давление 23 кПа? Плотность бетона 2,3 г/см3.

5.20 Латунный брусок с размерами 10 × 40 × 15 см, лежащий на столе, создает давление 34 кПа. Грань с какими ребрами находится внизу? Плотность латуни 8,5 г/см3.

5.21 Медный кубик с ребром 2 см лежит на оловянном кубике с ребром 4 см. Какое давление испытывает оловянный кубик? Стол под ним? Плотность олова 7,3 г/см3.

5.22 Оловянный кубик с ребром 4 см лежит на медном кубике с ребром 2 см. Какое давление испытывает медный кубик? Стол под медным кубиком?

5.23 Объем кубика увеличили в k = 27 раз, а его плотность уменьшили в т = 1,5 раза. Во сколько раз при этом изменилось давление кубика на стол?

5.24 Объем кубика уменьшили в т = 8 раз, а его плотность увеличили в k = 3 раза. Во сколько раз при этом изменилось давление кубика на стол?

5.25 Металлический куб массой 1 кг оказывает на стол давление 4,7 кПа. Из какого материала сделан куб?

5.26 Брусок массой 2 кг имеет форму параллелепипеда. Лежа на одной из граней, он оказывает давление 1 кПа, лежа на другой – давление 2 кПа, стоя на третьей – давление 4 кПа. Каковы размеры бруска?

5.27 Один литературный герой, закаляя свою волю, спал не доске, утыканной гвоздями (остриями вверх). Оцените, из скольких гвоздей должно было состоять ложе героя, считая, что масса героя 70 кг, острие каждого гвоздя имеет площадь 0,1 мм2, а человеческая кожа может выдержать давление 3 МПа.

5.28 На полу лежит плита, сделанная из материала плотностью ρ. Толщина плиты h. Какое давление p оказывает плита на пол?

5.29 На столе стоит сплошной медный куб. Какова масса куба, если он оказывает на стол давление 8 кПа?

5.30 Кубик сделан из материала с плотностью ρ = 2 г/см³. Внутри кубика имеется полость, объем которой составляет 25% объема кубика. Найдите ребро кубика, если он оказывает давление на стол равно р = 7 кПа.

5.31 Кубик с ребром а = 10 см имеет внутри себя полость, объем которой составляет 30% объема кубика. Найдите плотность кубика, если он оказывает давление на стол р = 900 Па.

5.32 Кубик с ребром а = 10 см стоит на столе. Каким должен быть объем воздушной полости внутри кубика, чтобы давление, оказываемое кубиком на стол, уменьшилось в 4 раза?

5.33 Сапоги, увязшие в размокшей глине, вытащить довольно трудно. Попробуйте объяснить это явление.

5.34 В сосуд налили керосин и воду. Толщина слоя нижней жидкости h1, = 1,5 см, верхней жидкости - h2 = 12 см. Сделайте пояснительный рисунок. Вычислите давление на дно сосуда.

5.35 В сосуд налили воду и ртуть. Толщина слоя верхней жидкости 4 см, а нижней - 1 см. Сделайте пояснительный рисунок. Определите давление на дно сосуда.

5.36 Корабль получил пробоину площадью 25 см² на глубине 3м. С какой силой нужно прижимать заглушку из трюма корабля, чтобы давление воды не выбило ее? Изменением давления в разных местах пробоины пренебречь.

5.37 На каждый квадратный сантиметр поверхности батискафа океан давит с силой 3кН. Оцените глубину, на которой находится батискаф.

5.38 Площадь дна кастрюли равна 1300 см². Вычислите, на сколько увеличится давление кастрюли на стол, если в нее налить 3,9 л воды.

5.39 Определите, с какой силой воздух давит на крышу дома размером 20 × 50 м при нормальном атмосферном давлении. Почему крыша не проваливается?

5.40 Проведённые с помощью манометра измерения давления жидкости на разных глубинах в открытом резервуаре дали следующие результаты: у дна резервуара давление составило Р1 = 34,8 кПа, а на расстоянии 1 м от дна составило Р2 = 27,8 кПа. Определите по этим данным плотность жидкости и высоту столба жидкости в резервуаре.

5.41 При атмосферном давлении, равном 751 мм рт. ст., манометр показывает давление в шинах автомобиля в 3,4 раза большее. С какой силой давит воздух на камеру автомобиля на каждые 100 см² её площади?

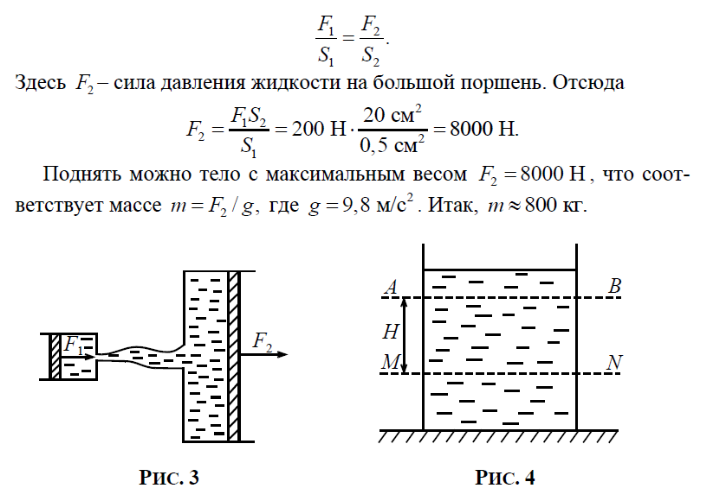
5.42 Каково давление воды на дно в точках А, В, С (Рис. 5.42)?

1. Качественные задачи:

Приложение 2

Задачи 7 класс

АРХИМЕДОВА СИЛА

ЗАДАЧИ I УРОВНЯ

1-1. Железобетонная плита размером 4 * 2 * 0,3 м полностью погружена в воду. Найдите архимедову силу, действующую на нее.

1-2. На стальной брусок, находящийся в нефти, действует архимедова сила, равная 120 Н. Определите объем бруска.

1-3. Чему равна архимедова сила, действующая на тело объемом 200 см3, если оно наполовину своего объема погружено в воду?

1-4. При полном погружении в жидкость на тело объемом 8 дм3 действует выталкивающая сила, равная 78,4 Н. Какая это жидкость?

1-5. Алюминиевый брусок размером 10 * 4 * 5 см погружен в керосин на 1/3 своего объема. Чему равна выталкивающая сила, действующая на брусок?

1-6. При полном погружении железного бруска в спирт его вес уменьшился на 160 Н. Каков объем этого бруска?

1-7. На камень, полностью погруженный в воду, действует выталкивающая сила, равная 25 Н. Определите объем камня.

1-8. На сколько гранитный булыжник объемом 5 дм3 будет легче в воде, чем в воздухе?

1-9. При взвешивании тела в воздухе динамометр показывает 4,4 Н, а в бензине он показывает 1,6 Н. Чему равен объем тела?

1-10. Вес тела равен 8 Н, а объем равен 400 см3. Тонет ли тело в воде, в спирте, в керосине?

1-11. Определите силу, которая необходима, чтобы удержать под водой пробковый пояс массой 2,5 кг, объем которого равен 15 дм3.

1-12. При погружении в воду вес железного якоря становится меньше на 150 Н. Определите объем якоря.

1-13. Какая требуется сила, чтобы удержать в воде металлический брусок массой 226 г и объемом 20 см3?

1-14. Плотность соленой воды в заливе Кара-Богаз-Гол в Каспийском море равна 1180 кг/м3. Чему равна выталкивающая сила, действующая на человека, если объем погруженной части тела воду равен 65 дм3?

1-15. Объем гранитной плиты массой 5,2 т равен 2 м3. Какую силу необходимо приложить к плите для подъема ее со дна водоема?

ЗАДАЧИ II УРОВНЯ

2-1. Тело массой 20 кг при погружении в воду вытесняет ее. Масса вытесненной воды равна кг. Определите, утонет ли это тело.

2-2. Пробковый пояс объемом 6,5 дм3 и массой 1,56 кг полностью погружен в воду. Какой по весу груз сможет удержать пояс на поверхности воды?

2-3. Массы алюминиевого и стального брусков одинаковы. Какое из этих тел легче удержать воде?

2-4. Определите вес соснового бревна, если оно плавает на поверхности воды, вытесняя при этом воду объемом 2,5 л.

2-5. Какую силу надо приложить, чтобы поднять под водой камень массой 30 кг и объемом 12 дм3?

2-6. Рассчитайте силу, которая потребуется, чтобы удержать плиту в воде. Гранитная плита имеет массу 2,6 т.

2-7. Алюминиевый брусок объемом 50 см3 взвешивают в керосине. Определите показания пружинных весов.

2-8. Тело объемом 5 дм3 имеет массу 5 кг. Тонет ли это тело в бензине, в воде, в керосине?

2-9. Спортсмен способен развить силу, равную 700 Н. Сможет ли он удержать в воде стальное ело, вес которого в воздухе равен 800 Н?

2-10. Трос лебедки выдерживает нагрузку 20 кН. Можно ли на этом тросе поднять в воде мраморную плиту объемом 2,5 м3?

2-12. Вес тела в воздухе равен 7,8 Н. При погружении в воду на него действует выталкивающая сила, равная 1 Н. Чему равна плотность тела?

2-13. Железное тело объемом 3 дм3 подвешено к динамометру. Что покажет динамометр, если тело опустить в воду наполовину его объема?

2-14. Для того чтобы сохранить нефть, ее в специальной оболочке опускают на дно моря. Определите массу груза, который потребуется, чтобы удержать нефть объемом 200 м3 под водой. Масса пустой оболочки равна 3 т, и она полностью заполнена нефтью.

2-15. При снятии груза осадка парохода уменьшилась на 10 см. Какой по весу груз сняли с парохода, если площадь горизонтального сечения парохода на уровне воды равна 4000 м2?

ЗАДАЧИ III УРОВНЯ

3-1. Какую силу надо приложить, чтобы удержать в воде камень массой 25 кг? Плотность камня равна 2500 кг/м3.

3-2. Кусок пробки плавает в баке с нефтью. Какая часть пробки погружена в нефть?

3-3. Рассчитайте подъемную силу пробкового спасательного круга массой 5 кг, плавающего в море.

3-4. Кусок дерева плавает в воде, погрузившись на 2/5 своего объема. Чему равна плотность дерева?

3-5. Плот состоит из десяти сухих еловых брусьев. Длина каждого бруса равна 5 м, шири¬на — 35 см и толщина — 25 см. Можно ли на этом плоту переправить через реку груз, вес которого равен 15 кН?

3-6. Аэростат объемом 4000 м3 наполнен гелием. Вес его конструкции вместе с оборудова¬нием и экипажем равен 30 кН. Гелий полностью заполняет баллоны на высоте, где плотность воздуха равна 1,2 кг/м3. Какой массы груз может поднять аэростат?

3-7. Тело плавает в жидкости, погружаясь на 1/5 своего объема. Определите отношение плотности жидкости к плотности тела.

3-8. Вес стального шара с воздушной полостью внутри в воде равен 12,2 Н, а в воздухе — 15,6 Н. Рассчитайте объем полости стального шара.

3-9. Вес однородного тела в воде в 3 раза меньше, чем в воздухе. Какова плотность тела?

3-10. Вес короны, масса которой равна 14,7 кг, равен 131,3 Н. Ответьте на вопрос: полностью ли корона золотая?

3-11. Штангист в воздухе поднимает штангу массой 200 кг. Какой массы камень поднимет этот штангист в воде? Плотность камня равна 2500 кг/м3.

3-12. Рассчитайте минимальный объем, который должна иметь подводная часть надувной резиновой лодки массой 10 кг, чтобы удержать на воде рыболова массой 70 кг.

3-13. Объем надводной части айсберга равен 5000 м3. Определите объем всего айсберга.

3-14. Подвешенный на пружине шарик опустили в воду. При этом растяжение пружины уменьшилось в 1,5 раза. Определите плотность материала, из которого сделан шарик.

3-15. Определите подъемную силу поплавка батискафа в морской воде, если объем поплавка равен 106 м и в нем содержится бензин плотностью 650 кг/м и объемом 86 м3. Масса пустого поплавка равна 15 т.

Приложение 2

Задачи 7 класс

Тема ФИЗИЧЕСКИЕ ТЕЛА. ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ

Уровень А

1.1 Вода в кастрюле закипела через 4,5 мин после включения плиты. Выразите это время в секундах и часах.

1.2 Масса мальчика равна 52 кг. Выразите массу мальчика в граммах, миллиграммах и тоннах.

1.3 Муравей прополз расстояние 46 см. Выразите это расстояние в метрах, километрах, миллиметрах и нанометрах.

1.4 Завтрак длился 0,15 ч. Выразите длительность завтрака в минутах и секундах.

1.5 Стороны прямоугольника равны а = 20 см и b = 1 м. Определите площадь прямоугольника. Ответ запишите в м2 и см2

1.6 Площадь прямоугольника S = 80 см2. Одна сторона прямоугольника равна а = 0,04 м. Найдите другую сторону прямоугольника. Ответ запишите в СИ.

1.7 По известной площади квадрата S = 81 мм2 определите его сторону. Ответ запишите в СИ.

1.8 Длина ребра куба равна 4 см. Определите объем этого куба. Ответ запишите в м3 и см3.

Уровень В

1.9 Представьте результаты измерений физических величин в единицах СИ. При необходимости (если получается много нулей в записи) перепишите результат в виде степени с основанием 10: а) радиус Земли 6400 км; б) масса груженого автомобиля с прицепом 8 т; в) радиус атома водорода 0,051 нм; г) масса пылинки 0,05 мкг; д) масса мальчика 60000 г; е) дорога от школы до дома занимает 18 мин.

1.10 Диаметр некоторой молекулы равен 2· см. Сколько таких молекул нужно «уложить» в ряд, чтобы длина полученной цепочки была равна 1 мм?

1.11 Площадь квадрата равна S = 25· см2. Чему равна сторона квадрата? Ответ запишите в СИ.

1.12 Куб имеет объем V = 8· мм3. Чему равна длина ребра куба? Ответ запишите в СИ.

1.13 Площадь основания цилиндрического сосуда S = 20 см2, а его высота Н = 0,3 м. Определите объем сосуда. Ответ запишите в м3 и см3.

1.14 Лист плотной бумаги в форме квадрата со стороной 1 м разрезали на 100 одинаковых маленьких квадратиков. Какова площадь и сторона одного квадратика? Сколько времени потребуется для укладки всех квадратиков в ряд вплотную друг к другу, если на укладку двух квадратиков уходит 5 с?

1.15 На поверхности воды разлилась нефть объемом V = 1 м3. Какую площадь займет нефтяное пятно, если толщина слоя нефти h = 2,5· мм?

1.16 Имелся квадрат площадью S = 100 см2. Сторону этого квадрата уменьшили в 2 раза - получился новый квадрат. Чему равны его площадь и сторона? Ответ запишите в СИ.

1.17 Цилиндрический сосуд имеет объем V= 9· Высота сосуда Н = 0,45 м. Определите площадь основания сосуда. Ответ запишите в м2 и см2

1.18 Из куба объемом V = 100 см3 сделали сто тысяч маленьких кубиков. Каким получился объем кубика? Какой длины ряд (в метрах) можно сложить из этих кубиков за время = 2 ч, если на укладку двух кубиков уходит время = 1 с?

1.19 Куб, объем которого V1 = 1 м3, разделили на кубики объемом V2 = 1 мм3 каждый. Сколько кубиков получилось? Определите время укладки этих кубиков в ряд, если на укладку 500 кубиков уходит время t = 8 мин.

Тема МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ

Уровень А

2.1. Велосипедист едет со скоростью 2,5 м/с. Выразите эту скорость в км/ч и в см/с. Какая система единиц измерения больше подходит к этому примеру?

2.2. Скорость первого объекта 15 м/с, а второго - 72 км/ч. Скорость какого объекта больше? Приведите примеры объектов, которые могут двигаться с такими скоростями.

2.3. Определите среднюю скорость самолета, который за промежуток времени 0,5 ч пролетел расстояние 250 км. Выразите эту скорость в м/с.

2.4. В течение 20 с автомобиль двигался равномерно со скоростью 72 км/ч. Какой путь проехал автомобиль за это время?

2.5. Трактор за первые 5 мин проехал 600 м. Какой путь он проходит за 0,5 ч, двигаясь с той же скоростью? Ответ запишите в метрах и в километрах.

2.6. Некоторый участок пути один велосипедист проехал за 10 с, двигаясь со скоростью 4 м/с. Другой велосипедист этот же участок пути проехал за 8 с. Какова средняя скорость второго велосипедиста на данном участке пути?

2.7. Поезд движется со скоростью 90 км/ч. За какое время мимо неподвижно стоящего на платформе пассажира проедут первые три вагона, если длина каждого вагона равна 24 м, а расстояние между вагонами равно 1 м? Ответ выразите в секундах.

2.8. При средней скорости 36 км/ч гружёный автомобиль совершает рейс за 40 мин. Сколько времени ему потребуется на обратный рейс при средней скорости 15 м/с ?

2.9. Человек стреляет из пистолета в мишень, находящуюся от него на расстоянии 33 м. Через какое время после выстрела, он услышит звук от удара пули в мишень, если скорость пули равна 660 м/с, а скорость распространения звука – 330 м/с?

2.10. Поезд движется со скоростью 80 км/ч. За какое время мимо неподвижно стоящего на платформе пассажира проедут последние четыре вагона, если длина каждого вагона равна 28 м, а расстояние между вагонами равно 1 м? Ответ выразите в секундах.

2.11. Поезд проходит мимо наблюдателя в течение 10 с, а по мосту длиной 400 м - в течение 30 с. Определить длину и скорость поезда.

2.12. В подрывной технике употребляют сгорающий с небольшой скоростью бикфордов шнур. Какой длины надо взять шнур, чтобы успеть отбежать на расстояние 300 м, после того, как его зажгут? Скорость бега 5 м/с, а пламя по шнуру распространяется со скоростью 0,8 см/с.

2.13. Вагон шириной 2,7 м пробит пулей, летящей перпендикулярно движению вагона. Смещение отверстий в стенках вагона относительно друг друга равно 3 см. Какова скорость движения пули внутри вагона, если вагон движется со скоростью 36 км/ч?

2.14. Велосипедист проехал полпути со скоростью 20 км/ч, а остаток пути прошел пешком. Какова была его скорость ходьбы, если ехал он 1/5 всего времени?

2.15. Мотоциклист за первые 10 мин проехал 5 км, а за следующие 8 мин - 9,6 км. Чему равна средняя скорость мотоциклиста на всем пути?

2.16. Определите среднюю скорость автобуса на всем пути, если первые 6 км пути он проехал за 0,2 ч, а следующие 10000 м пути - за 18 мин.

2.17. Расстояние между городами составляет 600 км. Одновременно из обоих городов навстречу друг другу выезжают два поезда, один со скоростью 80 км/ч, а другой – 70 км/ч. Определите место и время их встречи.

2.18. Два автомобиля движутся по дороге с постоянными скоростями 10 м/с и 54 км/ч. начальное расстояние между ними равно 1 км. Определите время, за которое второй автомобиль догонит первый.

2.19. Гепард, мчащийся со скоростью 108 км/ч, догоняет антилопу гну, которая находится в 100 м от него и убегает со скоростью 20 м/с. Через какое время произойдет их встреча?

2.20. Человек идет со скоростью 5,4 км/ч, делая 5 шагов за 2 с. Какова длина его шага?

2.21. С какой скоростью идет человек, если он делает 3 шага за 2 с и длина его шага равна 67 см?

Уровень В

2.22. Тело, двигаясь с некоторой скоростью, проходит путь = 0,2 км за время =50 с. Какой путь пройдет это тело за время = 20 с, двигаясь со скоростью в 2 раза большей, чем в первом случае?

2.23. Маленькая букашка ползет с постоянной скоростью по проволочному каркасу, имеющему форму квадрата. Время двух оборотов букашки t = 6 мин. Какое время затратит букашка на один оборот, если сторону квадрата уменьшить в п = 3 раза, а свою скорость букашка увеличит в k = 2 раза?

2.24. Человек полпути проехал на велосипеде со скоростью 25 км/ч, а остаток пути прошел пешком со скоростью 5 км/ч. Сколько времени он шел, если весь путь занял 3 ч.

2.25. Мотоциклист проехал 200 км. Половину всего времени движения он ехал со скоростью 60км/ч, а за оставшееся время он проехал 80 км. Какова его скорость на втором участке пути?

2.26. Автобус половину времени ехал со скоростью 40 км/ч, а оставшееся время – со скоростью 80 км/ч. Какую часть всего пути он ехал с большей скоростью?

2.27. Человек 3 км шел пешком, а потом 20 км ехал на велосипеде. Во сколько раз скорость езды больше скорости ходьбы, если ехал он вдвое дольше, чем шел?

2.28. Путешественник преодолел 240 км за 10 часов. Первую половину пути он ехал на автомобиле, а вторую - на слоне. С какой скоростью он ехал на слоне, если скорость автомобиля в 4 раза больше скорости слона?

2.29. Эхолот, установленный на всплывающем с постоянной скоростью v = 3 м/с батискафе, посылает короткий звуковой импульс. На какой глубине находился в этот момент эхолот, если глубина моря в месте погружения составляет H = 3 км, а отражённый от дна импульс был зарегистрирован эхолотом в момент его выхода на поверхность? Скорость звука в воде составляет vзв = 1500 м/с.

2.30. Пройдя 3/8 длины моста, собака услышала сигнал догоняющего ее автомобиля. Если собака побежит назад, то встретится с автомобилем у одного конца моста, а если побежит вперед, то встретится с ним у другого конца моста. Во сколько раз скорость автомобиля больше скорости собаки?

2.31. По дороге ползет удав длиной 12 м, а по удаву от головы к хвосту скачет попугай. Скорость удава относительно дороги 2 м/с, а скорость попугая относительно удава 3 м/с. Какой путь относительно дороги пройдет попугай, пока доберется от головы удава до его хвоста?

2.32. Товарный поезд проезжает мимо станции "Везенье" со скоростью = 36 км/ч. Через промежуток времени = 30 мин мимо этой станции в том же направлении проезжает экспресс со скоростью = 144 км/ч. На каком расстоянии от станции "Везенье" экспресс догонит товарный поезд?

2.33. Первый пешеход проходит расстояние S = 8 км между пунктами А и В за время = 2 ч, в второй - за время = 4 ч. На каком расстоянии от пункта А встретятся пешеходы, если выйдут одновременно навстречу друг другу из пунктов А и В? Скорости пешеходов постоянны.

2.34. Сколько времени пассажир, сидящий у окна поезда, движущегося со скоростью = 36 км/ч, будет видеть обгоняющий поезд длиной L = 100 м, идущий со скоростью = 72 км/ч?

2.35. По двум параллельным сторонам дороги едут навстречу друг другу грузовик и мотоцикл со скоростями = 10 м/с и = 54 км/ч, соответственно. В течение какого времени грузовик проезжает мимо мотоцикла, если длина грузовика = 20 м, а длина мотоцикла L2 = 2 м?

2.36. За время = 4 ч моторная лодка проходит по течению расстояние L = 48 км. За какое время она пройдет в обратном направлении половину этого расстояния, если скорость течения реки = 3км/ч.

2.37. За время = 1,5ч моторная лодка проходит против течения расстояние L = 18 км. За какое время она пройдет в обратном направлении вдвое большее расстояние, если скорость течения реки = 3км/ч.

2.38. Определите скорость течения воды в Волге на участке, где скорость грузового теплохода по течению равна 600 км/сут., а против течения - 336 км/сут.

2.39. На рис. 2.39 представлены графики зависимости пути от времени для двух автомобилей. Сколько времени потребуется первому автомобилю, чтобы догнать второй автомобиль, если они выехали одновременно в одном направлении, а первоначальное расстояние между ними было равно L = 40 км?

2.40. На рисунке 2.40 показаны графики зависимости скорости равномерного движения тел от времени. По этим графикам найдите: скорости движения каждого тела, рассчитайте пути, пройденные каждым телом за 4 с, постройте графики зависимости пути равномерного движения тел от времени.

2.41. На рис. 2.41 представлен график зависимости пути S, пройденного муравьем, от времени t. Определите скорость муравья на временных интервалах: (0; 3с), (3с; 4с), (4с; 6с) и среднюю скорость прохождения пути за время 5 с. .72. Из города по одной дороге одновременно выехали велосипедист и мотоциклист. Скорость велосипедиста 30 км/ч, мотоциклиста 90 км/ч. Постройте графики зависимости пути от времени для велосипедиста и мотоциклиста. Пользуясь графиком, найдите: а) какое расстояние будет между ними через 1 час после выезда; б) через какое время расстояние между ними будет равно 90 км?

2.42. Из населенного пункта по одной прямой дороге вышел путник и спустя 1,5 часа выехал всадник. Скорость путника 5 км/ч, скорость всадника 30 км/ч. Постройте графики зависимости пути от времени для путника и всадника и, пользуясь этими графиками, найдите, через какое время после начала своего движения всадник догонит путника.

2.43. Из города вышел турист, а через 3 часа вслед за ним по той же прямой дороге выехал велосипедист. Велосипедист едет со скоростью 30 км/ч, турист идет со скоростью 6 км/ч. Постройте графики зависимости пути от времени и, пользуясь ими, найдите, через какое время после выезда велосипедиста расстояние между велосипедистом и туристом будет равно 10 км.

2.44. Определите (Рис. 2.44) по графикам зависимости пути от времени с какими скоростями двигались автомобили 1 и 2? Чему равна скорость первого автомобиля по отношению ко второму?

2.45. Расстояние между городами 250 км. Одновременно из городов навстречу друг другу выезжают два автомобиля, один со скоростью 80 км/ч, другой – 90 км/ч. Построить графики движения и определить место и время встречи.

2.46. Автомобиль ехал 2 ч со скоростью 50 км/ч. потом 30 мин стоял, потом ехал 1 ч со скоростью 100 км/ч. Постройте графики зависимости скорости и пройденного пути от скорости.

2.47. На рисунке 2.47 изображены графики пути движения двух тел. На каком расстоянии от пункта отправления второго тела встретятся тела? На сколько позже начало движение второе тело? С какой скоростью двигалось второе тело? (ответ дать в м/с)

2.48. Черепаха ползла 10 с со скоростью 1 см/с, затем проползла 50 см за 10 с, потом 5 с стояла, потом проползла 20 см со скоростью 2 см/с. Сколько времени ползла черепаха? Постройте графики зависимости пути и скорости черепахи от времени.

2.49. Автомобиль проехал 100 м за 5 с, затем 200 м ехал со скоростью 10м/c, затем 4 с ехал со скоростью 54 км/ч. Каков путь, пройденный автомобилем? Постройте графики пути и скорости автомобиля от времени.

2.50. На рисунке 2.50 изображены графики пути движения двух поездов. Каково расстояние между пунктами, из которых вышли поезда? На сколько раньше вышел второй поезд? Через какое время от начала движения первого поезда встретились поезда? С какой скоростью двигался второй поезд? (ответ дать в м/с)

2.51. На рисунке 2.51 показаны графики зависимости пути равномерного движения тел от времени. По этим графикам определите: а) чему равны скорости движения тел; б) каковы пути, пройденные телами за 8 с, за 12 с; в) каким будет расстояние между телами через 8 с после начала движения?

2.52. На рисунке 2.52 изображен график зависимости пути от времени для некоторого тела. Постройте график зависимости скорости от времени.

2.53. На рисунке 2.53 изображен график зависимости скорости от времени для некоторого тела. Постройте график зависимости пути от времени.

2.54. На рисунке 2.54 показан график зависимости пути от времени для автобуса в течение трех часов движения. В течение четвертого часа автобус двигался с некоторой постоянной скоростью. Какова была эта скорость, если средняя скорость движения автобуса за 4 часа движения оказалась равной 25 км/ч?

2.55. Могут ли двигаться по одной железнодорожной колее в одну сторону два поезда, графики движения которых приведены на рис. а)? На рис. б)? В начальный момент времени первый поезд опережал второй на 20 км.

2.56. Человек ехал 1 час на велосипеде со скоростью 10 км/ч, потом 1 час отдыхал, потом ехал 1 час со скоростью 15 км/ч, потом 2 часа отдыхал, и, наконец, еще 1 час шел пешком со скоростью 5 км/ч. Постройте график зависимости пути от времени и, пользуясь им, найдите среднюю скорость движения на всем пути.

2.57. Первый пешеход проходит расстояние S = 4 км между пунктами А и В за время = 1 ч, в второй - за время = 3 ч. На каком расстоянии от пункта А встретятся пешеходы, если выйдут одновременно: первый из пункта А в направлении В, второй из В в направлении от А? Скорости пешеходов постоянны.

2.58. Из пунктов А и В в одном направлении одновременно выехали два автомобиля: легковой из пункта А и грузовой из пункта В. Расстояние между пунктами = 50 км. Скорость грузового автомобиля = 12 м/с. Определите скорость легкового автомобиля, если известно, что он догнал грузовой автомобиль на расстоянии L2 = 36 км от пункта В. Скорости автомобилей считать постоянными.

2.59. Из пунктов А и В навстречу друг другу одновременно выехали два автомобиля: грузовой из пункта А и легковой из пункта В. Известно, что встреча автомобилей произошла на расстоянии = 12,6 км от пункта А. Определите скорость легкового автомобиля, если расстояние между городами L = 41 км, а скорость грузового автомобиля = 14 м/с. Скорости автомобилей считать постоянными.

2.60. Два семиклассника движутся навстречу друг другу так, что за каждые = 10 с расстояние между ними уменьшается на = 16 м. Если же семиклассники будут двигаться в одном направлении, то за каждые = 5 с расстояние между ними будет увеличиваться на L2 = 3 м. Найдите скорости семиклассников.

2.61. Если два семиклассника от линии старта на стадионе побегут по кругу в одном направлении, то расстояние между ними будет увеличиваться за каждые = 2 с на = 4 м. Если же они побегут в разные стороны (один из них что-то перепутал), то за каждые = 3 с расстояние между ними будет увеличиваться на = 10 м. За какое время наиболее быстрый семиклассник вернется к линии старта, если длина беговой дорожки L = 300 м?

2.62. Из пунктов А и В навстречу друг другу одновременно выехали две машины. В промежуточном пункте С они встретились и продолжили свое движение. Первая машина (выехавшая из пункта А) приехала в пункт В через = 4 ч после встречи. Вторая машина приехала в пункт А спустя = 1 ч после встречи. Определите скорость второй машины, если скорость первой машины = 50 км/ч. Скорости машин считать постоянными.

2.63. Автомобиль 2 ч двигался со скоростью 15 м/с, а затем проехал еще 72 км со скоростью 20 м/с. Определите среднюю скорость автомобиля на всем пути.

2.64. Неопознанный летающий объект (НЛО), совершая разведывательный полет вокруг Земли с целью изучения интеллектуальных способностей учеников 7-го класса, двигался со скоростью = 7000 м/с в течение = 2 мин, затем со скоростью = 9000 м/с в течение = 3 мин. Напоследок он пролетел расстояние L = 600 км за время = 140 с. Определите среднюю скорость НЛО на всем пути.

2.65. Первую половину пути автомобиль проехал с постоянной скоростью = 50 км/ч, а вторую половину пути - с постоянной скоростью = 60 км/ч. Определите среднюю скорость автомобиля на всем пути.

2.66. Теплоход по течению двигался со скоростью 15 км/ч, а против течения - со скоростью 10 км/ч. С какой средней скоростью теплоход прошел весь путь туда и обратно, если расстояние между двумя пристанями равно 8 км?

2.67. Первую половину всего времени движения автомобиль проехал с постоянной скоростью = 50 км/ч, а вторую половину этого времени с постоянной скоростью = 60 км/ч. Определите среднюю скорость автомобиля за все время движения.

2.68. Автомобиль проехал две тpeтьи всего времени движения со скоростью = 54 км/ч, а остальное время - со скоростью = 10 м/с. Определите среднюю скорость автомобиля за всё время движения.

2.69. Автомобиль проехал первую четверть пути со скоростью = 18 м/с, а оставшийся участок пути - со скоростью = 72 км/ч. Определите среднюю скорость автомобиля на всем пути.

2.70. На прохождение некоторого расстояния ученик затрачивает время = 10 с. на прохождение в 5 раз большего расстояния тот же ученик затрачивает время на t = 15 с больше. Во сколько раз при этом увеличивается средняя скорость ученика?

2.71. Тело движется из пункта А в пункт В через промежуточный пункт С. Двигаясь из пункта А до пункта С с постоянной скоростью, тело проходит путь S = 3 км за время t = 1 ч. Увеличивая затем скорость в 3 раза, тело затрачивает на движение из С а В вдвое меньшее время. Чему равна средняя скорость тела при движении из пункта А в пункт В?

2.72. Средняя скорость мотоциклиста на всем пути = 90 км/ч. Первую треть пути мотоциклист проехал со скоростью = 60 км/ч. Определите скорость мотоциклиста на остальном пути.

2.73. Средняя скорость поезда на всем пути = 60 км/ч. Две трети пути поезд проехал со скоростью = 90 км/ч. Определите скорость поезда на остальном пути.

2.74. Каскадер увидел приближающийся к нему автомобиль и побежал навстречу ему со скоростью = 4м/с. Добежав до автомобиля, каскадер прыгает на его крышу и едет втрое большее время, чем бежал до автомобиля. Найдите среднюю скорость каскадера в указанном движении, если скорость автомобиля = 3 м/с.

2.75. Семиклассник проходит три одинаковых отрезка пути, увеличивая каждый раз время прохождения соответствующего участка пути вдвое. Скорость семиклассника на последнем отрезке пути = 0,7 м/с. Определите его среднюю скорость на всем пути.

2.76. Скорость автомобиля на первой половине пути = 20 м/с, а на второй половине пути = 10 м/с. Во сколько раз средняя скорость на первых 3/4 пути больше средней скорости на всем пути?

2.77. На первую треть пути автомобиль затратил четверть всего времени движения, а оставшееся расстояние он проехал со скоростью 40 км/ч. Какова средняя скорость автомобиля?

2.78. Винни Пух пошел в гости к Пятачку. Первую половину пути он шел со скоростью 20 см/с, вторую половину бежал со скоростью 30 см/с. С какой средней скоростью двигался Винни Пух? Постройте графики зависимости скорости от времени и средней скорости от времени.

Тема МАССА И ПЛОТНОСТЬ ФИЗИЧЕСКИХ ТЕЛ

Уровень А

3.1. Плотность некоторого вещества равна 2 г/см3. Выразите эту плотность в кг/м3.

3.2. Определите плотность металла массой 26,7 кг и объемом 3000 см3. Что это за металл?

3.3. В кузов одного автомобиля помещается 3 м3 песка. Какую массу песка увезут 20 таких автомобилей? Плотность песка 1,5 г/см3.

3.4. При строительстве железнодорожной линии вынули 6000 м3 грунта, плотность которого 1400 кг/м3. Сколько грузовых автомобилей можно нагрузить этим грунтом, если грузоподъемность одного автомобиля 12 т?

3.5. Определите массу медного бруска, имеющего длину 100 см, высоту 30 см и ширину 20 см.

3.6. На сколько масса 1 м3 воздуха меньше массы 1 дм3 алюминия? Плотность воздуха 1,29 кг/м3.

3.7. На прокатном стане прокатывают стальные листы размером 6 м × 15 м. Масса каждого листа 355,5 кг. Какова толщина одного стального листа?

3.8. Чтобы жесть, используемая для изготовления консервных банок, не ржавела, ее покрывают тонким слоем олова (лудят) из расчета 0,45 г олова на 200 см2 площади жести. Какова толщина слоя олова на жести?

Уровень В

3.9. Определите массу воды, полученной при таянии льда объемом 100 литров.

3.10. Определите массу льда, полученного при замерзании воды объемом 10л.

3.11. Определите массу изделия объемом V= 200 см3, если известно, что треть объема изделия выполнено из материала плотностью = 3000 кг/м3 , а остальная часть - из материала плотностью = 4500 кг/м3 .

3.12. Определите массу изделия объемом V = 300 см3 , если известно, что три четверти объема изделия выполнено из материала плотностью = 2000 кг/м3, а остальная часть - из материала плотностью = 6000 кг/м3

3.13. Два тела сделаны из одного и того же материала. При этом масса первого тела на т = 400 г меньше массы второго тела, а объем второго тела в 6 раз больше объема первого тела. Чему равна масса второго тела?

3.14. Два тела сделаны из одного и того же материала. При этом масса первого тела на т = 1 кг больше массы второго тела, а объем второго тела в 3 раза меньше объема первого тела. Чему равна масса второго тела?

3.15. Какова плотность сплава, изготовленного из V1 = 2 см3 золота и V2 = 5 см3 серебра? Плотность золота = 19,3 г/см3, серебра = 10,5 г/см3.

3.16. Масса сплошного куба, сделанного из некоторого вещества, равна 8 кг. Какую массу будет иметь куб из этого же вещества, но с вдвое меньшим ребром?

3.17. Масса сплошного куба, сделанного из некоторого вещества, равна 1 кг. Какую массу будет иметь куб из этого же вещества, у которого площадь одной боковой грани в 16 раз больше.

3.18. На поверхность воды разлили нефть массой т = 900 кг. Какую площадь займет нефть, если она растеклась тонким слоем толщиной d = 1/4000 мм? Ответ выразите в квадратных километрах.

3.19. Железный кубик с ребром а = 8 см снаружи покрыли тонким слоем олова массой т = 650 мг. Какова толщина слоя олова? Ответ выразите в миллиметрах.

3.20. Какую массу имеет сплошной куб, если площадь его поверхности S = 150 см2, а плотность вещества куба = 2700 кг/м3 ?

3.21. Слиток желтого металла неправильной формы осторожно окунули в литровую банку, наполненную водой. Когда слиток вынули, банка оказалась наполовину пустой. Может ли слиток быть золотым, если его масса 4,5 кг?

3.22. Найдите наружный объем стеклянного сосуда емкостью 1 литр, если его масса 400 г.

3.23. Стеклянная банка вмещает не более 3 л воды. Масса банки, целиком заполненной водой, составляет 4 кг. Определите объём стекла, из которого изготовлена банка. (ρстекла = 2500 кг/м3).

3.24. Имеются два сплошных куба, сделанные из одного и того же материала. Во сколько раз масса первого куба меньше, чем масса второго, если ребро первого куба в 3 раза меньше, чем ребро второго?

3.25. Какова масса сплошного алюминиевого куба, если площадь его поверхности 150 см2?

3.26. Полый медный куб с длиной ребра 6 см имеет массу 810 г. Какова толщина стенок куба?

3.27. Какой путь может проехать без заправки горючего автомобиль, если на 100 км пути его двигатель расходует 10 кг бензина, а вместимость его топливного бака 60 л?

3.28. Медную деталь массой 7,1 кг полностью погружают в бак, доверху наполненный керосином. Какова масса вылившегося керосина?

3.29. Определить объем полости пробки стеклянного графина, если при погружении в воду она вытесняет 50 г воды и имеет массу 100 г.

3.30. Какова плотность смеси из глицерина и спирта, если объем спирта составляет половину объема смеси? Как изменится ответ, если масса спирта составляет половину массы смеси?

3.31. Когда в наполненный доверху сосуд с водой опустили серебряную и медную детали, вылилось 80 г воды. Масса сосуда увеличилась при этом на 680 г. Каков объем каждой детали?

3.32. В кусок льда вмерз стальной шарик. Объем образовавшегося тела 50 см3, масса 114 г. Каков объем шарика?

3.33. Сплав состоит из олова массой 2,92 кг и свинца массой 1,13 кг. Какова плотность сплава, если считать, что объем сплава равным сумме объемов его составных частей.

3.34. Пробирка, наполненная водой, имеет массу 44 г. Эта же пробирка, но с кусочком стали массой 10 г, доверху заполненная водой, имеет массу 52,7 г. Определить плотность стали, помещенной в пробирку.

3.35. В куске кварца содержится небольшой самородок золота. Масса куска равна 100 г, его средняя плотность 8 г/см3. Определите массу золота, содержащегося в куске кварца, если плотность кварца 2,65 г/см3 , а плотность золота 19,4 г/см3.

3.36. Железная и алюминиевая детали имеют одинаковые объемы. Найти массы этих деталей, если масса железной детали на 12,75 г больше массы алюминиевой.

3.37. Имеются два бруска: медный и алюминиевый. Объем одного из этих брусков на 50 см3 больше, чем другого, а масса на 175 г меньше, чем масса другого. Каковы объемы и массы брусков?

3.38. Моток медной проволоки сечением 2,0 мм2 имеет массу 17,8 кг. Как, не разматывая моток, определить длину проволоки? Чему она равна?

3.39. С помощью медной проволоки хотят установить двухпроводную линию связи. Какой длины может быть эта линия, если моток проволоки имеет массу 1,5 кг, а когда проволоку виток к витку намотали на карандаш, 15 витков уложились на длине в 1 см?

3.40. Пластинки золота можно расплющивать до толщины 0,0001 мм. Какую площадь поверхности металла (дерева и т. д.) можно покрыть такими пластинками, изго¬товленными из золота массой 2,316 г?

3.41. Из пластмассы сделана уменьшенная в 3 раза копия медной статуэтки. Какова плотность этой пластмассы, если масса копии в 200 раз меньше массы статуи? Статуэтка и копия сплошные.

3.42. Масса второго бруска в 4 раза больше массы первого бруска, а объем второго бруска больше объема первого в 3 раза. По заданной плотности = 3 г/см3 второго бруска определите плотность первого бруска.

3.43. Масса первого бруска в 2 раза больше массы второго бруска, а объем второго бруска больше объема первого в 3 раза. По заданной плотности = 2,4 г/см3 первого бруска определите плотность второго бруска.

3.44. Первый брусок имеет массу т = 90 г. Второй брусок имеет высоту в 3 раза большую, длину в 6 раз меньшую, а ширину в 5 раз меньшую, чем у первого бруска. Определите массу второго бруска, если его плотность втрое больше, чем у первого бруска.

3.45. Первый брусок имеет массу т = 120 г. Второй брусок имеет высоту в 4 раза меньшую, длину в 3 раза меньшую, а ширину в 5 раз большую, чем у первого бруска. Определите массу второго бруска, если его плотность вдвое меньше, чем у первого бруска.

3.46. Масса первого изделия в 2 раза больше массы второго изделия, а их объемы находятся в соотношении V1: V2 = 1:3. Плотность первого изделия = 4 г/см3. Какова будет средняя плотность "составного" тела, если два изделия склеить? Массой и объемом клея пренебречь.

3.47. Масса первого изделия в 3 раза меньше массы второго изделия, а их объемы находятся в соотношении V1: V2 = 2: 1. Плотность первого тела = 1,8 г/см3. Какова будет средняя плотность "составного" тела, если два изделия склеить? Массой и объемом клея пренебречь.

3.48. Тело имеет массу т = 2 кг и объем V= 0,3 дм3. Треть объема тела заполнено веществом с плотностью = 2 г/см3. Какова плотность вещества, заполняющего остальной объем этого тела?

3.49. Кубик с ребром а = 20 см сделан из материала с плотностью = 3000 кг/м3. Однако внутри кубика имеется воздушная полость, поэтому его средняя плотность = 1200 кг/м3. Определите объем этой воздушной полости. Во сколько раз изменится средняя плотность кубика, если полость целиком заполнить водой? Массой воздуха внутри полости можно пренебречь.

3.50. Кубик изготовлен из материала с плотностью = 3 г/см3. В кубике сделали выемку, объем которой составляет 40 % объема кубика, и заполнили ее материалом с плотностью = 5 г/см3. Чему стала равна средняя плотность кубика?

Тема ВЗАИМОДЕЙСТВИЕ ТЕЛ. СИЛЫ ВЗАИМОДЕЙСТВИЯ.

Уровень А

4.1. На тело по вертикали действуют силы 5 Н и 15 Н. Изобразите эти силы. Сколько вариантов у Вас получилось?

4.2. На тело вдоль одной прямой действуют силы 2 Н и 3 Н. Может ли равнодействующая этих сил быть равной: а) 1 Н; б) 2 Н; в) 4 Н; г) 5 Н? Сделайте пояснительные рисунки.

4.3. Найдите равнодействующую сил, действующих вдоль одной прямой: а) 1 Н влево, 0,8 Н и 1,2 Н вправо; б) 6 Н вверх, 10 Н и 3 Н вниз.

4.4. Карлсон «завис» напротив окна Малыша. Масса Карлсона 100 кг. Какова подъемная сила моторчика Карлсона?

4.5. Перышко массой 0,03 г опускается вертикально вниз с постоянной скоростью. Чему равна сила сопротивления воздуха, действующая на перышко?

4.6. Пружина удлиняется на 1 см под действием силы 20 Н. Под действием какой силы эта пружина сожмется на 2,5 см?

4.7. Под действием силы F1 = 5 Н пружина удлинилась на х1 = 3 см. Чему будет равна длина пружины при действии на нее силы F2 = 15 Н, если длина недеформированной пружины равна L0 = 4 см?

4.8. Как, имея два одинаковых динамометра, определить массу груза, вес которого превышает предел измерения каждого из динамометров?

4.9. На тело действуют три силы, направленные вдоль одной прямой. Величины сил 3 Н, 12 Н и 6 Н соответственно. Какой может быть равнодействующая таких сил? Сделайте рисунок для каждого из возможных случаев.

4.10. Вагонетку тянут двое рабочих, прилагая к ней в одном направлении силы 30 Н и 45 Н. Сила сопротивления движению 15 Н. Чему равна равнодействующая всех сил, действующих на вагонетку? Изобразите силы графически.

4.11. Мальчик массой 50 кг надел на плечи рюкзак весом 50 Н. Начертить силы, действующие на мальчика. С какой силой он давит на пол?

4.12. К стоящей на полу гире массой 16 кг прикладывают направленную вверх силу 100 Н. Изобразите все силы, действующие на гирю. Чему равна каждая из них?

4.13. На ящик массой 20 кг, стоящий на полу оперся человек, прикладывая вниз силу 300 Н. Изобразите все силы, действующие на ящик.

4.14. Может ли мяч изменить направление полёта на противоположное, не сталкиваясь с препятствием? Объясните свой ответ.

4.15. Может ли тело массой 1 кг весить 20 Н?

4.16. К какому телу приложен: а) вес книги, лежащей на столе; б) вес мухи, ползущей по потолку?

4.17. Обладает ли весом тело, плавающее по поверхности воды?

4.18. Автомобиль массой 1000 кг движется равномерно по прямолинейному участку шоссе. Его двигатель развивают силу тяги 0,6 кН. Изобразите все силы, действующие на автомобиль. Сравните их по величине. Найдите равнодействующую этих сил.

4.19. Изобразите схематически все силы, действующие на автомобиль, разгоняющийся на горизонтальной дороге. Укажите физическую природу каждой силы.

4.20. На полке вагона поезда лежит пассажир, не касаясь стены вагона. Какая сила изменяет скорость пассажира, когда изменяется скорость поезда?

4.21. На горизонтальном участке пути трактор развил силу тяги 8 кН. Сила сопротивления движению трактора 6 кН. Вес трактора 40 кН. Изобразите эти силы графически.

4.22. Лестница у стены занимает положение, изображенное на рисунке. Изобразите схематически все силы, действующие на лестницу.

Уровень В

4.23. На медный шар объемом 120 см3 действует сила тяжести, равная 9 Н. Имеется ли внутри этого шара полость?

4.24. К бруску, покоящемуся на гладком горизонтальном столе, приложены три силы: F1 = 12 Н влево, а F2 и F3 вправо. Величина силы F3 в 3 раза больше F2. Будет ли это тело находиться в покое, если к нему приложить силу Fз, направленную влево, и направленную вправо силу F4, если величина силы F4 равна половине суммы сил F1 и F2? Все указанные силы направлены параллельно поверхности стола. Ответ обосновать.

4.25. Поезд весом Р = 20 МН движется по горизонтальному участку пути с постоянной скоростью. Определите силу тяги тепловоза, если сила трения составляет 0,5 % его веса.

4.26. Деревянный брусок под действием силы F= 12 Н движется по горизонтальной поверхности с постоянной скоростью. Во сколько раз сила трения меньше веса бруска, если масса бруска т = 3кг?

4.27. Известно, что вертикальная пружина растягивается на х = 2 см, если на нее действует сила F = 10 Н. На сколько растянется эта пружина, если к ней прикрепить ведро массой т = 0,2 кг и в него налить воду объемом V = 500 см3? Массой пружины пренебречь.

4.28. В бидон массой 500 г налили 4 л керосина. Какую силу надо приложить, чтобы поднять бидон?

4.29. В ведро, доверху наполненное водой, насыпали свинцовой дроби массой 3 кг. На сколько изменился вес ведра с его содержимым?

4.30. На полый оловянный куб с длиной ребра 10 см действует сила тяжести 51 Н. Каков объём полости?

4.31. При сжатии пружины на 3,5 см возникает сила упругости 1,4 кН. Какая сила возникнет при сжатии пружины на 2,1 см?

4.32. Под действием силы 4 Н пружина динамометра удлинилась на 5 мм. Какой массы груз надо подвесить к этой пружине, чтобы она удлинилась на 16 мм?

4.33. Если растягивать пружину силой 10 Н, её длина равна 16 см, если растягивать её силой 30 Н, её длина 20 см. Какова длина недеформированной пружины?

4.34. В нерастянутом состоянии пружина имела длину 88 мм, в результате её удлинения до 120 мм возникла сила упругости, равная 120 Н. Определите длину этой пружины в том случае, когда действующая сила равна 90 Н.

4.35. Если растягивать пружину силой 8 Н, длина пружины равна 14 см; если сжимать её силой 8 Н, длина пружины 10 см. Какова будет длина пружины, если сжимать её силой 4 Н?

4.36. Два человека тянут канат в противоположные стороны, каждый, прикладывая силу 200 Н. Какова сила натяжения каната?

4.37. К динамометру подвесили медную пластинку размерами 8 см × 3 см × 0,3 см, при этом пружина удлинилась на 1,9 см. Каково расстояние между делениями динамометра, если цена деления 0,1 Н?

4.38. Пружина под действием силы F1 = 150 Н, растянулась на х1 = = 1 см. Чему равно общее удлинение двух таких же пружин, соединенных как показано на рис. 4.12, под действием силы, величина которой F2 = 450 Н?

4.39. Пружина под действием силы, величина которой F1 = 50 Н, растянулась на х1 = 1 см. Чему равно общее удлинение двух таких же пружин, соединенных как показано на рис. 4.13, под действием силы, величина которой F2 = 250 Н?

4.40. Брусок массой т = 2 кг движется по горизонтальной поверхности с постоянной скоростью (рис. 4.14). В процессе движения на брусок действуют три силы со стороны привязанных к нему нитей: F1 = 4 Н, F2 = 8 Н, F3 = 6 Н. Определите силу трения, действующую на брусок, и силу давления бруска на поверхность.

4.41. Брусок массой т = 1 кг движется по горизонтальной поверхности с постоянной скоростью (рис. 4.15). В процессе движения на брусок действуют три силы со стороны привязанных к нему нитей: F1 = 2 Н, F2 = 5 Н, F3 = 2 Н. Определите силу трения, действующую на брусок, и силу давления бруска на поверхность.

4.42. Грузы подвешены на двух легких нитях так, как показано на рис. 4.16. Отношение сил натяжения верхней и нижней нитей F1/F2 =5. Определите отношение масс нижнего и верхнего грузов (m1/m2).

4.43. Грузы подвешены на двух легких нитях так, как показано на рис. 4.16. Отношение сил натяжения верхней и нижней F2/F1 =3. Определите массу нижнего груза, если сила натяжения верхней нити равна F2 = 1О Н.

4.44. Если груз аккуратно положить на вертикально установленную пружину, то она сожмется на х1 = 3 см. На сколько сожмутся две такие же пружины, если их установить так, как показано на рис. 4.17, и положить на них груз втрое меньшей массы?

4.45. Деревянный брусок с прикрепленными к нему тремя пружинами покоится на столе (рис. 4.18.) Пружины 2 и 3 сжаты на 1 см, а пружина 1 растянута на 2 см (относительно недеформированного состояния). В результате предварительных испытаний пружин установлено, что под действием силы 1 Н первая и третья растягиваются на 1 см, а вторая - на 2,5 мм. Изобразите силы, действующие на брусок. Определите силу трения, действующую на брусок, и силу давления бруска на стол. Масса бруска т = 1 кг.

4.46. В результате испытаний было установлено, что первая пружина под действием силы F1 = 18Н удлинилась на х1 = 2 см, а вторая пружина под действием силы F2 = 36 Н удлинилась на х2 = 1 см. Каково будет суммарное удлинение этих двух пружин, если их подвесить вертикально и прикрепить к ним грузы массой т1 = 4 кг и т2 = 6 кг так, как показано на рис. 4.19? Массой пружин пренебречь.

4.47. Первая пружина под действием силы F1 = 24 Н удлинилась на х1 = 1 см. Вторая пружина под действием силы F2 = 18 Н удлинилась на х2 = 2 см. Каково будет суммарное удлинение этих двух пружин, если их подвесить вертикально и прикрепить к ним грузы массой т1 = 2 кг и т2 = 3 кг так, как показано на рис. 4.20? Массой пружин пренебречь.

4.48. Когда брусок тянут вдоль поверхности стола, прикладывая горизонтальную силу 5 Н, он равномерно скользит по столу. Какая сила трения действует на брусок? Какова будет сила трения, если к покоящемуся бруску приложить горизонтальную силу 3 Н? 10 Н? Изобразите силы трения во всех трех случаях. Каким будет движение бруска в каждом из этих случаев?

4.49. На легких тросах подвешены два груза (см. рисунок). Масса первого груза 10 кг, второго – 20 кг. Повторите рисунок в тетради и изобразите на нем все силы, действующие на каждый из грузов. Какова сила натяжения троса в точке А? в точке В?

4.50. На столе лежит стопка из 7 одинаковых книг. В каком случае надо приложить меньшую силу: чтобы сдвинуть 6 верхних или вытянуть из стопки четвёртую сверху книгу, придерживая (но, не приподнимая) остальные?

4.51. На столе лежат три разных бруска. Чтобы сдвинуть верхний брусок, надо приложить силу 7 Н, а чтобы вытянуть средний, придерживая (но, не приподнимая) верхний, надо приложить силу 24 Н. Какую силу надо приложить, чтобы сдвинуть два верхних бруска вместе?

4.52. Два груза массами m1 = 200 г и m2 = 300 г соединены лёгкой пружиной и насажены на гладкую вертикальную спицу. Нижний конец спицы упирается в горизонтальную поверхность стола, груз массой m1 находится внизу (рис. а). При этом пружина сжата и её длина равна L1 = 12 см. Если конструкцию подвесить на нити, прикрепив её к грузу m2 (рис. б), то длина пружины станет равной L1 = 22 см. Какой будет длина пружины, если конструкцию подвесить на нити, прикреплённой аналогично, но только к грузу массой m1?

4.53. На одной чаше весов лежит кусок стекла массой 2,5 кг, на другой кусок серебра массой 2,1 кг. Какая чаша весов перетянет, если взвешивание производить в воздухе? в воде?

Тема ДАВЛЕНИЕ ТВЁРДЫХ ТЕЛ, ЖИДКОСТЕЙ И ГАЗОВ

Уровень А

5.1 Если стакан сдавливать ладонями за горлышко и дно, то на одной ладони появится отпечаток, а на другой - нет. Почему?

5.2 Является ли единицей измерения давления 1 мН/км2?

5.3 Расположите давления в порядке уменьшения: 6 кН/м2, 60 Н/см2, 600 Па, 60 кН/дм2, 60 Н/м2.

5.4 Тело находится в состоянии покоя на горизонтальной плоскости. Определить давление тела на эту плоскость. Масса тела т = 700 г. Площадь основания тела S = 35 см2.

5.5 Алюминиевый кубик с ребром 20 мм лежит на столе. Какое давление создает кубик?

5.6 Тело находится в состоянии покоя на горизонтальной плоскости. Давление тела на эту плоскость р = 2 кПа. Определить массу тела. Площадь основания тела S = 45 см2.

5.7 Какое давление на пол производит стол массой т = 20 кг, если площадь каждой из четырех ножек S = 5 см2? Влиянием атмосферного давления пренебречь.

5.8 Ветер создает давление всего лишь 80 Па. С какой силой ветер толкает вперед яхту с площадью паруса 60 м2?

5.9 Определите высоту столба керосина, который оказывает гидростатическое давление на дно сосуда равное 4 ·103 Па.

5.10 Найдите гидростатическое давление на дно сосуда цилиндрической формы с площадью основания 50 см2, в который налили 2 л воды.

5.11 В каком из сосудов сила давления жидкости на дно больше веса, а в каком – меньше?

5.12 С какой силой атмосферный воздух давит на бумажный лист, расположенный на горизонтальном столе? Размеры листа 16 × 20 см, атмосферное давление 1·105 Па.

5.13 Давление газа в баллоне 23 кПа. С какой силой газ давит на дно баллона площадью 3,2 дм2?

5.14 Высота столба ртути, уравновешивающего атмосферное давление, равна 760 мм. Во сколько раз будет больше высота столба воды, уравновешивающего это давление?

5.15 Во сколько раз высота столба жидкости в спиртовом барометре будет больше, чем в pтyтном барометре? Давление атмосферное. (ρртути = 13,6 г/см3 , ρспирта = 0,79 кг/дм3).

5.16 Водяной насос может создавать давление не более 220 кПа. На какую высоту он сможет подавать воду?

Уровень В

5.17 Какое наибольшее и наименьшее давления может создавать оловянный брусок с размерами 10×5×8 см?

5.18 Оловянный брусок с размерами 10 × 20 × 25 см и массой 5 кг лежит на столе своей большей гранью. Какое он создает давление?

5.19 Какая сторона бетонного блока с размерами 50 × 150 ×100 см опирается на землю, если блок создает давление 23 кПа? Плотность бетона 2,3 г/см3.

5.20 Латунный брусок с размерами 10 × 40 × 15 см, лежащий на столе, создает давление 34 кПа. Грань с какими ребрами находится внизу? Плотность латуни 8,5 г/см3.

5.21 Медный кубик с ребром 2 см лежит на оловянном кубике с ребром 4 см. Какое давление испытывает оловянный кубик? Стол под ним? Плотность олова 7,3 г/см3.

5.22 Оловянный кубик с ребром 4 см лежит на медном кубике с ребром 2 см. Какое давление испытывает медный кубик? Стол под медным кубиком?

5.23 Объем кубика увеличили в k = 27 раз, а его плотность уменьшили в т = 1,5 раза. Во сколько раз при этом изменилось давление кубика на стол?

5.24 Объем кубика уменьшили в т = 8 раз, а его плотность увеличили в k = 3 раза. Во сколько раз при этом изменилось давление кубика на стол?

5.25 Металлический куб массой 1 кг оказывает на стол давление 4,7 кПа. Из какого материала сделан куб?

5.26 Брусок массой 2 кг имеет форму параллелепипеда. Лежа на одной из граней, он оказывает давление 1 кПа, лежа на другой – давление 2 кПа, стоя на третьей – давление 4 кПа. Каковы размеры бруска?

5.27 Один литературный герой, закаляя свою волю, спал не доске, утыканной гвоздями (остриями вверх). Оцените, из скольких гвоздей должно было состоять ложе героя, считая, что масса героя 70 кг, острие каждого гвоздя имеет площадь 0,1 мм2, а человеческая кожа может выдержать давление 3 МПа.

5.28 На полу лежит плита, сделанная из материала плотностью ρ. Толщина плиты h. Какое давление p оказывает плита на пол?

5.29 На столе стоит сплошной медный куб. Какова масса куба, если он оказывает на стол давление 8 кПа?

5.30 Кубик сделан из материала с плотностью ρ = 2 г/см3. Внутри кубика имеется полость, объем которой составляет 25% объема кубика. Найдите ребро кубика, если он оказывает давление на стол равно р = 7 кПа.

5.31 Кубик с ребром а = 10 см имеет внутри себя полость, объем которой составляет 30% объема кубика. Найдите плотность кубика, если он оказывает давление на стол р = 900 Па.

5.32 Кубик с ребром а = 10 см стоит на столе. Каким должен быть объем воздушной полости внутри кубика, чтобы давление, оказываемое кубиком на стол, уменьшилось в 4 раза?

5.33 Сапоги, увязшие в размокшей глине, вытащить довольно трудно. Попробуйте объяснить это явление.

5.34 В сосуд налили керосин и воду. Толщина слоя нижней жидкости h1, = 1,5 см, верхней жидкости - h2 = 12 см. Сделайте пояснительный рисунок. Вычислите давление на дно сосуда.

5.35 В сосуд налили воду и ртуть. Толщина слоя верхней жидкости 4 см, а нижней - 1 см. Сделайте пояснительный рисунок. Определите давление на дно сосуда.

5.36 Корабль получил пробоину площадью 25 см2 на глубине 3м. С какой силой нужно прижимать заглушку из трюма корабля, чтобы давление воды не выбило ее? Изменением давления в разных местах пробоины пренебречь.

5.37 На каждый квадратный сантиметр поверхности батискафа океан давит с силой 3кН. Оцените глубину, на которой находится батискаф.

5.38 Площадь дна кастрюли равна 1300 см2. Вычислите, на сколько увеличится давление кастрюли на стол, если в нее налить 3,9 л воды.

5.39 Определите, с какой силой воздух давит на крышу дома размером 20 × 50 м при нормальном атмосферном давлении. Почему крыша не проваливается?

5.40 Проведённые с помощью манометра измерения давления жидкости на разных глубинах в открытом резервуаре дали следующие результаты: у дна резервуара давление составило Р1 = 34,8 кПа, а на расстоянии 1 м от дна составило Р2 = 27,8 кПа. Определите по этим данным плотность жидкости и высоту столба жидкости в резервуаре.

5.41 При атмосферном давлении, равном 751 мм рт. ст., манометр показывает давление в шинах автомобиля в 3,4 раза большее. С какой силой давит воздух на камеру автомобиля на каждые 100 см2 её площади?

5.42 Каково давление воды на дно в точках А, В, С (Рис. 5.42)?

5.43 Сосуд с водой имеет форму, изображённую на рисунке 5.43. Площадь дна сосуда 100 см2, площадь поршня 200 см2, сила, с которой вода действует на поршень, равна 100 Н. Чему равна сила давления воды на дно сосуда, если h = 50 см?

5.44 Два тяжелых поршня соединены между собой стержнем длиной l (Рис. 5.44). Площадь меньшего поршня S, площадь большего 2S. Найдите давление на больший поршень, если общая масса поршней и стержня М, а плотность жидкости ρ.

5.45 Герметичный сосуд полностью заполнен водой (Рис. 5.45). На лёгкий поршень площадью S давят рукой с силой F.Поршень может свободно перемещаться и находится на расстояниях H1 от верхней части сосуда и H2 от дна, считая по вертикали. Атмосферное давление Pа. Найти давление вблизи верхней части сосуда и дна.

5.46 В цилиндрический сосуд налили масло до высоты h1 = 60 см. До какой высоты нужно налить воду в другой сосуд, площадь основания которого в четыре раза меньше, чтобы давление на дно было таким же, как и в первом сосуде? Плотность масла ρ1 =0,9г/см3, воды ρ2 = 1 г/см3.

5.47 В цилиндрический сосуд налили воду до высоты hl = 40 см. До какой высоты нужно налить керосин в другой сосуд, площадь основания которого в два раза больше, чтобы сила давления на дно была такой же, как и в первом сосуде? Плотность воды ρ1 = 1 г/см3, керосина ρ2 = 0,8 г/см3.

5.48 В цилиндрический сосуд налиты равные массы воды и керосина. Определите гидростатическое давление на дно сосуда, если высота столба керосина hк = 10 см. Плотность воды ρв = 1000 кг/м3 , плотность керосина ρк = 800 кг/м3. Во сколько раз изменится полученный ответ, если массу воды увеличить в 2 раза, а массу керосина оставить прежней?

5.49 В цилиндрический сосуд налиты равные массы воды и керосина. Определите гидростатическое давление на дно сосуда, если высота столба воды hв = 12 см. Плотность воды ρв = 1г/см3, плотность керосина ρк = 800 кг/м3 . Во сколько раз изменится полученный вами ответ, если массу керосина увеличить в 2 раза, а массу воды оставить прежней?

5.50 В цилиндрическом сосуде слой воды толщиной h = 30 см плотно закрыт поршнем массой т = 3 кг. Плотность воды ρв = 1 г/см3. Площадь дна сосуда S = 30 см2. Определите давление на дно сосуда. Атмосферное давление не учитывать.

5.51 В цилиндрическом сосуде слой воды толщиной h = 50 см плотно закрыт невесомым поршнем, на который действует направленная вертикально вниз сила F = 10 Н. Плотность воды ρв = l г/см3. Площадь дна сосуда S = 25 см2. Определите давление на дно сосуда. Атмосферное давление не учитывать.

5.52 Длина аквариума а = 40 см, ширина b = 20 см, а высота h = 30 см. Определите силу, действующую на все боковые стенки аквариума. Аквариум полностью заполнен водой.

5.53 Длина аквариума а = 50 см, ширина b = 30 см. Аквариум наполовину заполнен водой. Сила, действующая на одну боковую сторону аквариума, равна F = 180 Н. Определите высоту аквариума.

5.54 В сосуд высотой Н = 60 см, в основании которого квадрат со стороной а = 10 см, доверху налили воду и масло. Высота столба масла Н1 = 20 см, плотность воды ρ2 = 1 г/см3, плотность масла ρ1= 0,9 г/см3. Определите гидростатическое давление на дно сосуда и силу гидростатического давления, действующую на боковую поверхность сосуда.

5.55 В сосуд высотой Н = 50 см, в основании которого квадрат со стороной а = 20 см, доверху налили воду и керосин. Высота столба воды Н1 = 20 см, плотность воды ρ1 = 1 г/см3, плотность керосина ρ2 = 0,8 г/см3. Определите гидростатическое давление на дно сосуда и силу гидростатического давления, действующую на боковую поверхность сосуда.

5.56 На столе находятся стопка из пяти кирпичей массой m = 1 кг каждый и пустой цилиндрический сосуд массой М = 1 кг. В сосуд начинают аккуратно наливать воду с расходом q = 1О см3/с. Через какое время давления кирпичей и сосуда на стол сравняются? Чему при этом будет равна высота столба воды в сосуде? Площадь основания кирпича S1 = 200 см2. Площадь поперечного сечения сосуда, измеренная по внешнему диаметру сосуда S2 = 50 см2, по внутреннему диаметру – S3= 40 см2. Плотность воды ρ = 1 г/см3.

5.57 На столе находится цилиндрический сосуд массой М = 3 кг, в который налили воду высотой h1 = 50 см. Площадь поперечного сечения сосуда, измеренная по внешнему диаметру сосуда, S2 = 40 см2, по внутреннему диаметру - S1 = 20 см2. Рядом на стол вплотную друг на друга начинают укладывать стальные листы. Какова должна быть толщина слоя стальных листов, при которой давления на стол с их стороны и со стороны сосуда с водой сравняются? Сколько листов окажется в стопке, если толщина одного листа d = 5 мм? Плотность воды ρв = 1 г/см3, плотность стали ρс = 8 г/см3.

5.58 В цилиндрическом сосуде слой воды плотно закрыт невесомым тонким поршнем, на который действует направленная вертикально вниз сила F = 20 Н. Сила тяжести, действующая на воду, в 2 раза больше силы F, а площадь дна в 4 раза больше площади боковой поверхности цилиндра. С какой силой действует вода на боковую поверхность цилиндра? Атмосферное давление не учитывать.

5.59 Резервуар кубической формы заполняют водой с помощью шланга, имеющего площадь поперечного сечения S = 4 см2. Скорость истечения воды из шланга v = 1 м/с. Определите время заполнения резервуара водой, если известно, что в конце заполнения сила, действующая со стороны воды на одну боковую стенку резервуара, равна F = 72 кН. Плотность воды ρ = 1 г/см3.

5.60 Аквариум, в основании которого квадрат, заполняют, наливая ежесекундно q = 10 г/с воды. Определите время заполнения аквариума водой (целиком), если известно, что моменту заполнения половины аквариума на каждую боковую стенку аквариума действовала сила F = 600 Н. Высота аквариума в 2 раза больше стороны основания.

5.61 В цилиндрическую вертикальную трубку налили доверху масло и воду. Масса воды в два раза меньше массы масла. Какую часть трубки занимает вода? Чему равно гидростатическое давление на дно трубки, если посередине ее давление pc = 2,4 кПа? Плотность масла ρм = 0,8 г/см3, плотность воды ρв = 1 г/см3.

5.62 В цилиндрическую вертикальную трубку налили доверху ртуть и воду в равных по массе количествах. Какую часть трубки занимает ртуть? Чему равно гидростатическое давление на дно трубки, если посередине ее давление pc = 5 кПа? Плотность ртути ρрт=13,6г/см3, плотность воды ρв = 1 г/см3.

5.63 Сосуд квадратного сечения полностью заполнен взятыми в равных по массе количествах водой и керосином. Определите давление на расстоянии от дна сосуда, равном 1/5 его высоты. Масса воды т = 1 кг, площадь основания S = 10 см2.

5.64 Цилиндрический сосуд полностью заполнен взятыми в равных по массе количествах водой и керосином. Определите давление на расстоянии от дна сосуда, равном 1/6 его высоты. Масса воды т = 2 кг, площадь основания S = 20 см2.

5.65 В вертикальную цилиндрическую трубку, снизу закрытую пробкой, наливают воду. Пробка с площадью поперечного сечения S = 8 см2 вылетает, когда масса воды становится равной т = 300 г. Чему равна площадь поперечного сечения трубки, если максимальная сила трения, действующая на пробку, равна F= 1,2 Н? Толщиной стенок трубки пренебречь.

5.66 Вертикальная трубка с закрытым концом, частично наполненная керосином, опущена открытым концом в сосуд с керосином. При этом уровень керосина в трубке на 15 см выше уровня керосина в сосуде. Определите давление воздуха в трубке, если наружное давление р0=103360 Па.

5.67 В мензурке находятся три слоя жидкостей (ртуть, вода и машинное масло) толщиной по 20 см. На какой глубине давление равно 7,9 кПа? Атмосферное давление не учитывайте.

5.68 В цилиндрический сосуд налиты ртуть и вода. Общая высота двух слоев жидкости 14,6 см, а давление на дно сосуда 2,7 кПа. Каково отношение масс ртути и воды?

5.69 Сосуд в форме куба с ребром а = 36 см заполнен водой и керосином. Масса воды равна массе керосина. Определите давление жидкостей на дно сосуда. (Толщиной стенок сосуда пренебречь.)

5.70 Аквариум, имеющий форму куба, полностью заполнен водой. Во сколько раз отличаются силы давления на дно аквариума и на его стенку?

5.71 Аквариум имеет форму куба с длиной ребра 24 см. При какой толщине слоя воды сила давления на дно будет в 8 раз больше, чем на стенку?

5.72 Сила давления воды на дно прямоугольного аквариума равна 60 Н. На меньшую из боковых стенок, ширина которой 20 см, вода давит с силой 10 Н. Какова сила давления на большую из боковых стенок? Атмосферное давление не учитывайте.

5.73 В цилиндрический сосуд налиты три несмешивающиеся жидкости: четырёххлористый углерод, вода и керосин. Определите давление на дно сосуда, если массы всех жидкостей одинаковы, а верхний уровень наиболее лёгкой жидкости – керосина – находится на высоте 23 см от дна сосуда. Плотности жидкостей равны соответственно 1,6 г/см3, 1г/см3, 0,8 г/см3.

5.74 Концы U-образной трубки на h = 30 см выше уровня воды в ней. Левую трубку целиком заполнили керосином. Определите массу залитого в трубку керосина. Плотность воды ρв = 1 г/см3, плотность керосина ρк = 0,8 г/см3, площадь сечения трубки S = 3 см2 .

5.75 U-образная трубка частично заполнена водой. В правое колено наливают керосина столько, что он образует столб высотой h = 30 см. На сколько повысится уровень воды в левом колене трубки? Плотность воды ρв = 1 г/см3, плотность керосина ρк = 0,8 г/см3.

5.76 В сообщающиеся сосуды площадью сечения S1 = 150 см2 и S2 = 100 см2 налита вода. Сосуды сверху закрыты поршнями массами т1 = 2 кг и т2 = 1 кг. Когда на второй поршень положили перегрузок, оказалось, что уровень воды в сосудах одинаков. Какой будет разность высот воды в сосудах, если перегрузок положить на первый поршень? Плотность воды ρв = 1 г/см3.

5.77 В сообщающиеся сосуды площадью сечения S1= 100 см2 и S2 = 200 см2 налита вода. Сосуды сверху закрыты поршнями массами т1= 1 кг и т2 = 3 кг. Когда на первый поршень положили перегрузок, оказалось, что уровень воды в сосудах одинаков. Какой будет разность высот воды в сосудах, если перегрузок положить на второй поршень? Плотность воды ρв = 1 г/см3.

5.78 В U-образной трубке находится ртуть, вода и керосин (Рис. 5.78). Найдите высоту столбов воды и керосина, если в правом колене трубки уровень ртути на 1 см выше, чем в левом.

5.79 В левом колене заполненных водой сообщающихся сосудов находится слой керосина высотой 10 см. В каком из колен уровень жидкости выше? На сколько?

5.80 В U-образную трубку с площадью поперечного сечения S = 8 см2 налиты ртуть, вода и масло. Высота слоя воды в левом колене трубки h. = 10 см. В правом колене трубки уровень ртути на b = 0,6 см выше, чем в левом. Определите массу содержимого трубки, если масса ртути mрт= 150 г. Плотность ртути ρрт = 13,6 г/см3, масла ρм = 0,8 г/см3.

5.81 В U-образной трубке находится ртуть. В правое колено трубки доливают воду, и уровень ртути в левом колене поднимается на 1 см. Какова высота слоя воды?

5.82 После доливания в левое колено U-образной трубки с водой 25-сантиметрового слоя легкой жидкости уровень воды в правом колене поднялся на 10 см. Какова плотность долитой жидкости?

5.83 Концы U-образной трубки на h=30 см выше уровня воды в ней. Левую трубку целиком заполнили керосином. Определите высоту столба керосина Н в трубке.

5.84 В сообщающихся сосудах, площади сечения которых относятся как 3 : 1, находится вода. В узкий сосуд доливают слой керосина высотой 25 см. На сколько поднимется уровень воды в широком сосуде?

5.85 В сосуде с водой на подставках находится цилиндр без дна. Высота выступающей из воды части цилиндра равна Н = 5 см. Внутрь цилиндра наливают масло. Какую высоту должен иметь цилиндр, чтобы его можно было заполнить маслом целиком?

5.86 В каком сосуде раньше начнут появляться пузырьки воздуха, если дуть в трубку с двумя ответвлениями (см. рисунок)? Какое избыточное давление нужно создать в трубке для выдувания первых пузырьков, если h1= 30 см, h2= 20 см? Какая жидкость раньше попадет в верхнюю часть трубки, если не дуть в неё, а втягивать воздух?

5.87 Гидравлический пресс имеет поршни с площадью S1 = 0,003 м2 и S2 = 400 cм2. На больший поршень действует сила F = 1000 Н. Какая сила действует на меньший поршень?

5.88 Гидравлический пресс имеет поршни с площадью S1 = 200 cм2 и S2 = 0,15 м2. На меньший поршень действует сила F = 100 Н. Какая сила действует на больший поршень?

5.89 В гидравлической машине, состоящей из малого и большого поршней, малый поршень под действием силы F1 = 200 Н опустился на h1 = 8 см. При этом большой поршень поднялся на h2 = 2 см. Какая сила действовала на большой поршень?

5.90 Гидравлическая машина, состоит из одного малого и двух больших поршней. Малый поршень под действием силы F1= 400 Н опустился на h1 = 10 см. При этом каждый большой поршень поднялся на h2 = 2 см. Какая сила действует на каждый из больших поршней?

5.91 При равновесии поршень в первом из сообщающихся сосудов (см. рисунок) устанавливается на 20 см выше, чем во втором. Массы поршней m1= 2 кг и m2= 4 кг. Если на первый поршень поставить гирю массой 3 кг, то поршни установятся на одинаковой высоте. Как расположатся поршни, если гирю переставить на второй поршень?

Тема РАБОТА. МОЩНОСТЬ. ПРОСТЫЕ МЕХАНИЗМЫ

Уровень А

6.1. Является ли единицей механической работы 1 кН·мм?

6.2. Какие измерительные приборы нужно иметь для определения работы по подъему ведра с пола на табурет?

6.3. Какие силы совершают механическую работу в следующих ситуациях: а) теннисный мяч падает на землю; б) автомобиль, движущийся по горизонтальной поверхности, останавливается? Определите знаки работы показанных вами сил.

6.4. Мальчик передвинул игрушечный автомобиль по полу на 90 см, прикладывая к веревке горизонтальную силу 2 Н. Какую работу совершил мальчик?

6.5. Какую работу совершит насос мощностью 500 Вт за 10 минут?

6.6. Насосу с мощностью 1,5 кВт нужно выполнить работу 900 кДж. Сколько времени он должен работать?

6.7. К точке А рычага приложена сила F = 20 Н (рис. 6.7). Какую силу надо приложить к рычагу в точке В, чтобы он находился в равновесии?

6.8. К точке А рычага приложена сила F = 20 Н (рис. 6.8). Какую силу надо приложить к рычагу в точке В, чтобы он находился в равновесии?

6.9. С какой силой надо тянуть за кольцо А, чтобы поднять груз весом 250 Н (рис. 6.9)?

6.10. Какую силу F надо приложить к свободному концу нити, чтобы удерживать груз весом 8 Н (рис. 6.10)?

6.11. Чему равна мощность двигателя автомобиля, если развивая силу тяги 700 Н, он движется со средней скоростью 72 км/ч?

6.12. Какая работа совершается при подъёме гранитной плиты объёмом 2 м3 на высоту 12 м?

6.13. Чему равно давление под поршнем площадью 20 см2, если при подъёме поршня на 15 см сила давления газа совершила работу 210 Дж?

6.14. Пожарный насос развивает мощность 3 кВт. На какой этаж он может подавать ежеминутно 1200 л воды? Расстояние между этажами 3 м.

6.15. Гружёный автомобиль массой 5 т, перемещаясь равномерно по горизонтальному участку дороги, проехал расстояние 2 км. Какую работу совершил двигатель автомобиля, если сила трения составляет 0,001 силы тяжести автомобиля?

6.16. Тепловоз мощностью 3 МВт тянет состав, прилагая силу 150 кН. Какое потребуется время для равномерного прохождения этим составом пути 48 км?

6.17. С какой постоянной скоростью ехал автомобиль массой 1 т, если за 30 мин его двигатель совершил работу 18 МДж, а сила сопротивления движению равна 5% веса автомобиля?

6.18. Вычислите мощность насоса, подающего ежеминутно 1300 л воды на высоту 24м.

6.19. Высота плотины гидроэлектростанции 12 м, мощность водяного потока 3 МВт. Найдите объём воды, падающей с плотины за 1 мин.

6.20. КПД наклонной плоскости равен 40 %. При поднятии по ней груза совершили работу 500 Дж. Чему равна полезная работа при поднятии груза?

6.21. Лебедка, совершив работу 400 кДж, протянула завязший грузовик на расстояние 4 м при силе натяжения троса 80 кН. Определите КПД лебедки.

6.22. Вес груза 40 кН. Лифт поднял его на высоту 7 м. Чему равен КПД лифта, если его двигатель совершил работу 300 кДж?

6.23. Мощность двигателя подвесной канатной дороги 4 кВт. Для равномерного подъема кабины с пассажирами общей массой 2,1 т двигателю потребовалось 18 мин. Определите КПД двигателя канатной дороги, если кабина поднимается на высоту 105 м.

6.24. Вертолету массой 1,4 т требуется 1,5 мин, чтобы равномерно подняться на высоту 350 м. Чему равна мощность двигателя вертолета, если его кпд равен 30 %.

Уровень В

6.25. Девочка каждый раз прилагает горизонтально направленную силу F, чтобы передвинуть (не переворачивая) по горизонтальной поверхности ящик массой т = 30 кг. Сила трения, действующая на ящик, Fтр= 150 Н. В каких пределах может изменяться сила F, если ящик переворачивается при силе F0 = 350 Н? Какую работу совершит девочка, переместив ящик на d = 2 м, действую на него силой F = 250 Н?

6.26. Девочка каждый раз прилагает вертикально направленную силу F = 50 Н, чтобы поднять с земли различные камни на высоту Н = 90 см. В каких пределах может изменяться масса каждого из камней? Какую работу совершит девочка при подъеме камня массой т = 2 кг?

6.27. Первый мотор поднимает груз массой m1 со скоростью v1 , а второй поднимает груз массой m2 со скоростью v2. С какой скоростью v будет поднимать груз массой M мотор, мощность которого равна сумме мощностей первых двух моторов?

6.28. При помощи гидравлического пресса нужно поднять груз массой т = 100 т. Определите число ходов малого поршня за t = 1 мин, если за один ход он опускается на глубину Н = 20 см. Мощность двигателя, приводящего в движение малый поршень пресса, равна N = 3,68 кВт, а его КПД 75 %. Отношение площадей поршней пресса равно k = 0,01.

6.29. Какую работу надо совершить, чтобы поставить вертикально рельс массой 100 кг и длиной 4 м, лежащий на земле?

6.30. Какую работу нужно совершить, чтобы поднять из колодца глубиной 30 м ведро с водой? Масса цепи равна 8 кг, масса ведра с водой 10 кг. Размерами ведра можно пренебречь.

6.31. Определите мощность потока воды, протекающей через плотину, если высота падения воды Н = 25 м, а ее расход q = 120 м3/мин. Плотность воды ρ = 1 г/см3. Сколько килограммов льда можно расплавить с помощью всей энергии, полученной от этой плотины за 1 ч, если для плавления 100 г льда требуется 34 кДж энергии? КПД этого процесса 10%.

6.32. Башенный кран поднимает в горизонтальном положении бетонную балку длиной L= 5 м и поперечным сечением S = 100 см2. Какую мощность развивает кран при равномерном подъеме балки на высоту H = 12 м за время t = 1 мин.? Плотность бетона ρ = 2,7 г/см3. Сколько придется заплатить «энергетикам» за произведенную краном работу, если 1 кВт·ч (киловатт-час) электроэнергии стоит 2 рубля, а КПД крана 10 %?

6.33. По наклонному настилу длиной L = 3 м рабочий вкатил в кузов бочку массой т=55кг. Определите КПД погрузки, если рабочий прилагал параллельную настилу силу F = 330 Н, а высота кузова машины Н = 1,5м.

6.34. Длина прямого подъема на дороге составляет L= 800 м. Верхняя его точка возвышается на H = 11 м над подножием. Грузовик тянет прицеп с силой F= 3,2 кН. Определите КПД подъема прицепа по дороге, если масса прицепа т = 6 т.

6.35. Масса первого груза (Рис.6.35) 1 кг, масса третьего груза 2 кг. Какова масса второго груза?

6.36. Масса первого груза (Рис.6.36) 5 кг, масса рычага 2 кг. Какова масса второго груза?

6.37. Массы всех трех грузов (Рис.6.37) равны по 4 кг. Какова масса рычага?

6.38. Плечи рычага, находящегося в равновесии, соответственно равны 15 и 90 см. Меньшая сила, действующая на рычаг, равна 1,2 Н. Найдите большую силу. Какой выигрыш можно получить с помощью этого рычага в силе? в работе?

6.39. На левом конце рычага подвешен груз объемом V, = 1 дм3, а на правом - объемом V2 = 2500 см3. Плотность левого груза ρ1 = 3 г/см3, плотность правого – ρ2 = 2000 кг/м3. Определите длину рычага, если длина его левого плеча L1 = 20 см. Массой рычага пренебречь.

6.40. На левом конце рычага подвешен груз объемом V1 = 1500 см3, а на правом - объемом V2 = 4 дм3. Плотность левого груза ρ1 = 1500 кг/м3, плотность правого - ρ2 = 4 г/см3. Определите длину рычага, если длина его правого плеча L2 = 0,1 м. Массой рычага пренебречь.

6.41. К концам горизонтально расположенного рычага прикреплены грузы, объемы которых находятся в соотношении V1: V2 = 3: 7. Каково отношение плотностей грузов, если длина левого плеча рычага L1 = 10 см, а правого плеча L2 = 25 см?

6.42. С помощью устройства, содержащего подвижный и неподвижный блоки, поднимают груз массой т = 150 кг. При этом на свободный конец троса действуют силой F = 937,5 Н. Изобразите схему такого устройства. Определите КПД этого устройства. Какой выигрыш в работе дает устройство, если груз поднимают на высоту Н = 2 м?

6.43. На концах доски длиной L = 6 м стоят мальчики, массы которых т1 = 70 кг и т2=50 кг. Посередине доски находится опора. Мальчики начинают аккуратно двигаться к середине доски со скоростями ʋ1 = 20 см/с и ʋ2 = 15 см/с. Через какое время доска окажется в горизонтальном положении? Массой доски пренебречь.

6.44. Посередине доски массой т = 40 кг вплотную друг к другу стоят мальчики. Массы мальчиков т1 = 40 кг и т2 = 50 кг. Посередине доски находится опора, правее которой на L0 =1 м расположен центр тяжести доски. Мальчики начинают аккуратно двигаться к краям доски со скоростями ʋ1= 10 см/с и ʋ2= 20 см/с. Через какое время доска займет горизонтальное положение?

6.45. Стержень, на одном конце которого подвешен груз весом 120 Н, находится в равновесии в горизонтальном положении, если его подпереть на расстоянии 1/5 длины стержня от груза. Чему равен вес стержня?

6.46. На концах рычага действуют силы 2 и 18 Н. Длина рычага 1 м. Где находится точка опоры, если рычаг в равновесии?

6.47. Чтобы приподнять один конец доски, лежащей на полу, надо приложить силу 300 Н. Какова масса доски?

6.48. Чтобы измерить массу линейки, на один из её концов положили грузик массой 15 г и начали выдвигать этот конец за край стола. Линейка находилась в равновесии до тех пор, пока её не выдвинули на треть длины. Чему равна масса линейки?

6.49. Прямолинейный кусок проволоки массой 40 г подвешен за середину. Левую половину куска согнули, как показано на рисунке. Какой массы грузик надо подвесить в точке А, чтобы восстановить равновесие.

6.50. К концам рычага приложены направленные вниз силы 6 Н и 4 Н. Точка опоры находится на 5 см ближе к одному концу рычага, чем к другому. Какова длина рычага, если он находится в равновесии?

6.51. Если груз лежит на левой чаше неравноплечих весов, его уравновешивают гири массой 9 кг на правой чаше. Если же груз переложить на правую чашу, его уравновешивают гири массой 25 кг на левой чаше. Какова масса груза?

6.52. Стержень массой 9 кг и длиной 1 м лежит на двух опорах. Одна из них находится у левого края стержня, а другая на расстоянии 10 см от правого края. С какой силой действует на стержень каждая из опор?

6.53. Однородный стержень длиной 1 м подвешен горизонтально на двух динамометрах. Первый динамометр находится на расстоянии 10 см от левого конца стержня и показывает 20 Н, второй динамометр находится на расстоянии 30 см от правого конца. Какова масса стержня?

6.54. Прямой кусок проволоки массой 200 г подвешен на нити за середину и находится в равновесии. Левый конец куска согнули в средней части так, что он составил прямой угол с другой частью проволоки. Какую силу нужно приложить к правому концу проволоки, чтобы восстановить равновесие?

6.55. К однородной балке массой 400 кг и длиной 7 м подвешен груз массой 700 кг на расстоянии 2 м от одного из концов. Балка концами лежит на опорах. Какова сила давления на каждую из опор?

6.56. Какого веса груз можно поднять при помощи подвижного блока весом 40 Н, если тянуть веревку с силой 0,23 кН?

6.57. Поднимет ли стоящий на полу человек весом 600 Н при помощи неподвижного блока груз массой 72 кг?

6.58. С помощью подвижного блока поднимают в течение 0,5 мин ящик с кирпичами на высоту 12 м, действуя с силой 320 Н. Как велика мощность, развиваемая при подъеме ящика?

6.59. Груз какой массы можно поднять с помощью устройства, состоящего из подвижного и неподвижного блоков, если к свободному концу веревки приложить силу F = 210 Н. Вес подвижного блока Р = 20 Н. Изобразите схему этого устройства. Трение не учитывать.

6.60. К рычагу необходимо подвесить грузы с массами т1 = 100 г, т2 = 360 г и т3=400 г так, чтобы он находился в равновесии (рис. 6.60). Массой рычага и крючков пренебречь. Ответ пояснить. Положение крючков не менять.

6.61. К рычагу необходимо подвесить грузы с массами т1 = 50 г, т2 = 300 г и т3 =600г так, чтобы он находился в равновесии (рис. 6.61). Массой рычага и крючков пренебречь. Ответ пояснить. Положение крючков не менять.

6.62. На каком расстоянии от опоры следует подвесить груз массой т2 = 18 кг, чтобы рычаг находился в горизонтальном положении (рис. 6.62)? Сила F = 40 Н, масса т1 = 60 кг, длина левого плеча рычага L1 = 10 см, длина правого плеча рычага L2 = 30 см. Массой рычага и блока пренебречь.

6.63. В изображенной на рис. 6.63 системе стержень длиной 5D находится в равновесии. Диаметр каждого блока равен D. Масса груза 3 равна 12 кг. Чему равна масса груза 1? Массой стержня, нитей и блоков пренебречь.

6.64. В изображенной на рис. 6.64 системе стержень длиной 7D находится в равновесии. Диаметр каждого блока равен D. Масса груза 2 равна 4 кг. Чему равна масса груза 3? Массой стержня, нитей и блоков пренебречь.

6.65. Как надо соединить подвижные и неподвижные блоки, используя их минимальное число, чтобы получить выигрыш в силе в 3 раза? Нарисуйте схему устройства и подтвердите расчетом. Трением и массой блоков пренебречь.

6.66. Как надо соединить подвижные и неподвижные блоки, используя их минимальное число, чтобы получить выигрыш в силе в 5 раз? Нарисуйте схему устройства и подтвердите расчетом. Трением и массой блоков пренебречь.

6.67. Однородный стержень длиной L = 90 см укреплен при помощи нити и опоры, как показано на рис. 6.67. При каком расстоянии х от правого конца стержня до опоры сила натяжения нити в 4 раза меньше силы тяжести, действующей на стержень?

6.68. В системе, изображенной на рис. 6.68, определите давление груза массой 2т на стол. Масса меньшего груза равна 2 кг, площадь основания большего груза S = 200 см2.

6.69. С помощью устройства, содержащего подвижный и неподвижный блоки, поднимают груз массой т = 150 кг. При этом на свободный конец троса действуют силой F = 937,5 Н. Изобразите схему такого устройства. Определите КПД этого устройства. Какой выигрыш в работе дает устройство, если груз поднимают на высоту Н = 2 м?

6.70. Разработайте устройство для подъема грузов, дающее выигрыш в силе в три раза. Оно должно содержать рычаг длиной 1 м и неподвижный блок. Масса поднимаемого груза много больше масс рычага и блока. Приведите схему устройства, на которой укажите длины плеч рычага. Какое давление на пол оказывает человек, использующий это устройство для подъема груза весом Р = 300 Н, если масса человека m = 70 кг, а площадь подошв его обуви S = 400 см2?

6.71. Груз массой m = 1,5 кг поднимают на высоту Н = 2 м с помощью наклонной плоскости и блока (рис. 6.71). Длина доски L = 8 м. Сила, приложенная к грузу при таком перемещении, равна F = 6 Н. КПД подъемного устройства 40%. Каков при этом КПД блока?

6.72. Для облегчения подъема грузов часто применяют приспособление, схематически показанное на рисунке 6.72. Верхние блоки один относительно другого неподвижны. Цепочка, соединяющая блоки, не проскальзывает. Какую силу F надо приложить к цепочке, чтобы груз находился в равновесии? Верхние блоки имеют радиусы соответственно R и r. Весом нижнего блока и трением пренебречь.

6.73. Для облегчения подъема грузов часто применяют ворот, состоящий из двух валов, неподвижно закрепленных на одной оси (рис. 6.73). При работе такого ворота трос (или цепочка), сматываясь с одного вала, одновременно наматывается на другой. Какую силу F нужно приложить к рукоятке ворота, чтобы груз находился в равновесии? Весом блока и трением пренебречь.

6.74. Определите силу, действующую в точке закрепления блоков к потолку, если груз массой m=75 кг, подвешенный к блоку (рис. 6.74), удерживается на весу человеком, который тянет за веревку вертикально вниз.

Задачи 8 класс

Равномерное движение. Средняя скорость

1.1. В течение какого времени пассажир, сидящий у окна поезда, идущего со скоростью 54 км/ч, будет видеть проходящий мимо него встречный поезд, скорость которого 36 км/ч, а длина 150 м? (6 с)

1.2. По двум параллельным путям в одном и том же направлении идут два поезда: то-варный длиной 630 м со скоростью 48,6 км/ч и электропоезд длиной 120 м со скоростью 102,6 км/ч. В течение какого времени электропоезд будет обгонять товарный? (50 с)

1.3. Поезд длиной 240 м, двигаясь равномерно, прошел мост за 2 минуты. Какова ско-рость поезда, если длина моста 360 м? (5 м/с)

1.4. Пассажирский поезд проходит мимо столба за 6 с. За какое время пройдут друг мимо друга пассажирский и скорый поезда, если скорость скорого поезда в 1,5 раза больше скорости пассажирского, а длина пассажирского на треть больше длины скорого? (4 с)

1.5. Водитель легкового автомобиля начинает обгон трейлера на скорости 90 км/ч в момент, когда расстояние между машинами равно 20 м, и перестраивается в прежний ряд при расстоянии между машинами 15 м. Определить время маневра. Скорость трейлера 72 км/ч, длина легкового автомобиля 4 м, длина трейлера 16 м. (11 с)

1.6. Катер идет по течению реки из пункта А в пункт В 3 часа, а обратно - 6 часов. За какое время проплывет расстояние АВ упавший в воду спасательный круг? (12 ч)

1.7. Между двумя пунктами, расположенными на реке на расстоянии 100 км друг от друга, курсирует катер. Катер проходит это расстояние по течению за 4 ч, а против течения - за 10 ч. Определить скорость течения реки и скорость катера относительно воды. (7,5 км/ч; 17,5 км/ч)

1.8. Скорость движения лодки относительно воды в 2 раза больше скорости течения ре-ки. Во сколько раз больше времени занимает поездка на лодке между двумя пунктами про-тив течения, чем по течению? (3)

1.9. Из середины колонны автомобилей, движущейся со скоростью 10 км/ч, одновре-менно выезжают два мотоциклиста: один в голову колонны, другой - в хвост. С какой скоростью двигались мотоциклисты, если их скорости были одинаковыми, а время движения одного мотоциклиста оказалось в два раза меньше другого? (30 км/ч)

1.10. Рыбак плывет на лодке вверх по реке. Проезжая под мостом, он уронил в воду за-пасное весло. Через час он обнаружил потерю и, повернув обратно, догнал весло в 6 км ни-же моста. Какова скорость течения реки, если рыбак все время греб одинаково? (3 км/ч)

1.11. Из одного города в другой вышел пешеход. Когда он прошел 27 км, вслед ему вы-ехал автомобиль, имеющий скорость в 10 раз большую. Второго города оба достигли одно-временно. Найти расстояние между городами. (30 км)

1.12. Автомобиль движется от моста со скоростью 72 км/ч. В начальный момент расстояние от автомобиля до моста равно 200 м. На каком расстоянии от моста будет автомобиль через 10 с? (400 м)

1.13. Мимо бензоколонки прошел грузовой автомобиль со скоростью 54 км/ч. Через два часа мимо той же бензоколонки в том же направлении прошел легковой автомобиль со скоростью 72 км/ч. Через какое время после этого и на каком расстоянии от бензоколонки легковой автомобиль догонит грузовой? (6 ч; 432 км)

1.14. Мимо бензоколонки прошел грузовой автомобиль со скоростью 54 км/ч. Через два часа в противоположном направлении мимо той же бензоколонки прошел легковой автомо-биль со скоростью 72 км/ч. На каком расстоянии от бензоколонки автомобили встретились? (≈ 61,7 км)

1.15. Первый пешеход идет из одной деревни в другую 10 часов, а второй - 15 часов. Че-рез сколько часов встретятся пешеходы, если одновременно выйдут навстречу друг другу из этих деревень? (6 ч)

1.16. Человека, идущего вдоль трамвайных путей, каждые 7 мин обгоняет трамвай, а каждые 5 мин попадается трамвай навстречу. С каким интервалом трамваи отходят от оста-новки? (5 мин 50 сек)

1.17. Пешеход проходит расстояние между пунктами А и В за 1 час, а автомобиль про-езжает его за 10 мин. Однажды пешеход вышел из А в В, но на половине пути его догнал автомобиль и вторую половину пешеход проехал. За какое время пешеход в этот раз добрался до пункта В? (35 мин)

1.18. Из пункта А в пункт В одновременно выезжают две машины: первая со скоростью 50 км/ч, вторая со скоростью 40 км/ч. Первая, доехав до В, поворачивает обратно. Вторую машину первая встретила в 6 километрах от В. Найти расстояние АВ. (54 км)

1.19. Два спортсмена побежали одновременно в одном направлении вокруг стадиона. Один из них пробегает за минуту 400 м, а второй - 300 м. Путь вокруг стадиона равен 1500 м. Через сколько минут они опять сойдутся вместе и сколько кругов вокруг стадиона к этому времени сделает каждый? (15 мин; 3 и 4 круга)

1.20. Петров и Иванов бегают по гаревой дорожке стадиона длиной 400 м. Петров про-бегает круг за 50 с, а Иванов за 60 с. Сколько раз они встретятся при забеге на дистанцию 4 км, если они стартуют одновременно и бегут в одну сторону? (1)

1.21. Автомобиль «Волга» может проехать 39 км от Барнаула до Бобровки со скоростью 100 км/ч, а «Тойота» - целых 180 км/ч. Какой автомобиль доедет до Бобровки первым, если примерно посередине дороги есть 3 км плохой дороги, по которой «Волга» может ехать со скоростью 25 км/ч, а «Тойота» - только 10 км/ч? («Волга»)

1.22. Двa aвтoмoбиля oднoвpeмeннo выexaли из пyнктa A. Пepвый вce вpeмя двигaлcя co cкopocтью 72 км/чac, a втopoй, пpoexaв 30 км co cкopocтью 60 км/чac, yвeличил cкopocть и пpoйдя еще 30 км дoгнaл пepвый aвтoмoбиль. Кaкoвa cкopocть втopoгo aвтoмoбиля нa втоpoм отрезке пути? (90 км/ч)

1.23. Автомобиль проезжает от А до В за 1 час. Автомобиль выехал из А и одновремен-но из В вышел пешеход. Автомобиль встретил пешехода, довез его до А и поехал опять в В, затратив на всю дорогу 2 ч 40 мин. За какое время расстояние АВ проходит пешеход? (5 ч)

1.24. Три грузовика возят песок из пункта А в пункт В. Из пункта А они отправляются с интервалом в 1 час. Скорость груженого грузовика равна 30 км/ч. Разгрузившись в пункте В грузовики возвращаются обратно со скоростью 50 км/ч. Первый грузовик на обратном пути из В в А встречает два других. Через какое время после встречи с третьим грузовиком первый вернется в пункт А, если расстояние АВ равно 100 км? (1,25 ч)

1.25. Ровно в 12.00 дядя Федор отправился на электричке из Москвы в Простоквашино. В то же самое время из Простоквашино в Москву на скором поезде отправился кот Матроскин. На промежуточной станции Матроскин увидел дядю Федора и быстро перебежал к нему в электричку. Успеют ли они к обеду, приготовленному Шариком к 14.00, если известно, что скорость поезда на 20% больше скорости электрички, а встретились они в 13.00. (Не ус-пеют)

1.26. Два велосипедиста едут со скоростью 35 км/ч. Один из них увеличивает скорость до 45 км/ч, едет с этой скорость 10 км и поворачивает обратно. Через какое время после раз-ворота велосипедисты встретились? (100 с)

1.27. По дороге идет пешеход со скоростью 5 км/ч. Его обгоняет велосипедист, движу-щийся со скоростью 15 км/ч. Велосипедист доехал до библиотеки, пробыл там 15 мин, с прежней скоростью поехал обратно и опять встретил пешехода. С момента обгона пешехода до момента встречи с ним прошел один час. Через сколько времени после встречи с велосипедистом пешеход дойдет до библиотеки? (37,5 мин)

1.28. Автомобиль поехал из города А в город В по прямой дороге. При этом первую треть пути он ехал по грунтовой дороге со скоростью 30 км/ч, а оставшееся расстояние по проселочной дороге со скоростью 10 км/ч. Обратно автомобиль поехал в объезд по асфаль-тированной дороге со скоростью 70 км/ч и затратил на обратный путь на 1 час меньше. На сколько дорога в объезд длиннее прямой дороги, если по прямой расстояние АВ равно 100 км? (≈ 374 км)

1.29. Если Петя в школу идет пешком, то тратит на дорогу 20 мин, а если едет на автобусе - то 5 мин. Однажды Петя пошел в школу пешком, но по дороге вспомнил, что забыл дома дневник. Вернувшись обратно и второй раз выйдя из дома, Петя сел в автобус и затратил на весь путь 20 мин. Какую часть пути Петя прошел к моменту, когда вспомнил про дневник? (0,375)

1.30. Колонна автомобилей длиной 500 м движется со скоростью 40 км/ч. От головной машины отъехал мотоциклист со скоростью 80 км/ч, доехал до хвостовой машины и сразу возвратился обратно. Какое расстояние проехал мотоциклист за это время? (≈ 1,33 км)

1.31. Два поезда одновременно выехали из пунктов А и В навстречу друг другу. Первый поезд прибыл в пункт В через 4 часа после встречи поездов, а второй в пункт А через 9 часов после встречи. Сколько часов был в пути первый поезд? (10 ч)

1.32. Два человека одновременно вступают на эскалатор с противоположных сторон и движутся навстречу друг другу с одинаковыми скоростями относительно эскалатора 2 м/с. На каком расстоянии от входа на эскалатор они встретятся, если длина эскалатора 100 м, а его скорость 1,5 м/с? (87,5 м)

1.33. Человек взбегает вверх по движущемуся вниз эскалатору за 1 минуту, а по движу-щемуся вверх эскалатору - за 20 с. За какое время поднимется вверх стоящий на эскалаторе человек? Скорости эскалатора и бегущего человека постоянны. (1 мин)

1.34. Двигаясь по движущемуся эскалатору метро, человек проходит его за 60 с, а двига-ясь с той же скоростью в обратном направлении - за 120 с. Определить скорость эскалатора и скорость движения человека, если длина эскалатора равна 120 м. (0,5 м/с; 1,5 м/с)

1.35. Две электрички длиной 200 м каждая движутся навстречу друг другу. Скорость од-ной из них меньше, чем второй, и равна 40 км/ч. Расстояние между местом встречи первых вагонов и расставания последних равно 40 м. Найти скорость второй электрички. (60 км/ч)

1.36. По дороге едет колонна автомобилей со скоростью 20 км/ч. Из середины колонны одновременно отправляются два мотоциклиста: один в голову колонны, а другой в хвост. Первый мотоциклист приехал к месту на 6 минут позже второго. Какова длина колонны, если скорость мотоциклистов равна 30 км/ч? (2,5 км)

1.37. Два тела движутся равномерно навстречу друг другу и расстояние между ними уменьшается на 16 м за каждые 10 с. Если эти тела с такими же скоростями движутся в од-ном направлении, то расстояние между ними увеличивается на 3 м за каждые 5 с. Найти скорость каждого тела. (1,1 м/с; 0,5 м/с)

1.38. Из пунктов А и В, расстояние между которыми равно 22,4 км, одновременно выез-жают два велосипедиста. Если они поедут навстречу друг другу, то встретятся через 0,5 часа, а если поедут в одном направлении, то один догонит второго через 3,5 часа. Найти скорости велосипедистов. (25,6 км/ч; 19,2 км/ч)

1.39. Мотоциклист за первые два часа проехал 90 км, а следующие три часа двигался со скоростью 50 км/ч. Какова средняя скорость на всем пути? (48 км/ч)

1.40. Два автобуса выехали одновременно из пункта А в пункт В. Один из них первую половину пути ехал со скоростью v1, а вторую половину со скоростью v2. Второй автобус двигался со скоростью v1 половину времени своего движения от А к В, а вторую половину - со скоростью v2. Определить среднюю скорость движения каждого автобуса, если v1 = 30 км/ч, а v2 = 50 км/ч. (37,5 км/ч; 40 км/ч)

1.41. Поезд первую половину пути проехал со скоростью 72 км/ч, а вторую половину - в 1,5 раза медленнее. Определить среднюю скорость на всем пути. (16 м/с)

1.42. Велосипедист на стадионе первые 10 кругов едет со скоростью 20 км/ч, а следую-щие 5 кругов - со скоростью 40 км/ч. Какова средняя скорость движения велосипедиста? (24 км/ч)

1.43. Средняя скорость автомобиля равна 15 м/с. С какой скоростью двигался автомо-биль первые 6 с, если за остальные 12 с он прошел расстояние 150 м? (20 м/с)

1.44. Мотоциклист проехал пятую часть расстояния между двумя пунктами со скоро-стью 10 м/с, а оставшуюся часть пути – со скоростью 20 м/с. Определить все расстояние, ес-ли время движения мотоциклиста 1 ч. (60 км)

1.45. Первые 20 минут тело двигалось со скоростью 5 м/с, а затем еще некоторое время со скоростью 20 м/с. Найти это время, если средняя скорость тела оказалась равна 15 м/с. (40 мин)

1.46. На дорогу от Москвы до Кубинки (65 км) пассажир электрички тратит 1 ч 10 мин. Средняя скорость электрички на перегонах между платформами 70 км/ч. Сколько времени электричка стоит на остановках? (≈ 14,3 мин)

1.47. Автомобиль едет из пункта А в пункт В со скоростью 60 км/ч. В пункте В он оста-навливается на время, равное 1/4 времени движения из А в В, и возвращается обратно со скоростью 45 км/ч. Определить среднюю скорость автомобиля на всем пути. (≈ 46,5 км/ч)

1.48. Автомобиль ехал половину времени со скоростью 60 км/ч, половину оставшегося времени со скоростью 45 км/ч, а оставшийся путь - со скоростью 75 км/ч. Найти среднюю скорость движения автомобиля. (60 км/ч)

1.49. Автомобиль 1/3 часть пути проехал со скоростью 60 км/ч, следующую четверть пути - со скоростью 75 км/ч и оставшуюся часть - со скоростью 50 км/ч. Определить среднюю скорость автомобиля. (≈ 58,1 км/ч)

1.50. Велосипедист проехал половину пути со скоростью 12 км/ч, следующую треть пу-ти - со скоростью 15 км/ч и оставшиеся 36 км он проехал за 2 ч. Определить среднюю ско-рость велосипедиста и расстояние, которое он проехал. (≈ 13,7 км/ч; 216 км)

1.51. Автомобиль проехал расстояние 30 км со скоростью 10 м/с, затем разгрузился и вернулся в начальный пункт со средней путевой скоростью 20 м/с. Определить время раз-грузки, если средняя путевая скорость на всем пути была равна 8 м/с. (50 мин)

1.52. Катер прошел первую половину пути со скоростью в два раза большей чем вторую. Средняя скорость на всем пути составила 1 м/с. Найти скорость катера на первой половине пути. (1,5 м/с)

1.53. Самолет первую треть пути летел со скоростью 700 км/ч, вторую треть – со скоро-стью 500 км/ч, а остаток пути – со скоростью, вдвое большей средней скорости на первых двух участках. Найти среднюю скорость самолета. (700 км/ч)

1.54. Автобус ехал 3 ч по шоссе, 1,5 ч по грунтовой дороге и еще 0,5 ч по проселочной дороге. Скорость автобуса по грунтовой дороге в 2 раза больше скорости по проселочной дороге, а скорость по шоссе в 3,5 раза больше, чем скорость по проселочной дороге. Найти скорость автобуса по проселочной дороге, если средняя скорость на всем пути равна 33,6 км/ч. (12 км/ч)

1.55. Катер проходит расстояние между пунктами А и В на реке по течению за время 3 ч, а против течения - за 6 ч. Средняя скорость катера при движении от А к В и обратно равна 10 км/ч. Найти собственную скорость катера и скорость течения реки. (vк = 11,25 км/ч; vр = 3,75 км/ч)

1.56. Автомобиль едет из одного города в другой со скоростью, зависимость которой от времени представлена на рис. 1.1. Определить среднюю скорость автомобиля. (21,4 км/ч)

1.57. На рис. 1.2 представлен график зависимости скорости автомобиля от времени. Определить среднюю скорость автомобиля на всем пути. (≈ 48,9 км/ч)

1.58. На рис. 1.3 представлена зависимость скорости автомобиля от времени. При этом средняя скорость автомобиля оказалась равна 30 км/ч. Определить скорость автомобиля на участке равномерного движения. (40 км/ч)

1.59. Из пункта А в пункт В автомобиль едет с горы со скоростью в два раза большей, чем обратно в гору. На дорогу из А в В автомобиль затрачивает 1 час. Какова средняя ско-рость автомобиля из А в В и сразу обратно, если расстояние АВ равно 60 км. (40 км/ч)

1.60. Велосипедист едет из одного города в другой. Первую четверть пути он ехал со скоростью 30 км/ч, последнюю четверть - со скоростью 10 км/ч, а в промежутке - со скоро-стью 15 км/ч. Определить среднюю скорость велосипедиста. (15 км/ч)

1.61. Бегун, стартовавший на дистанцию 5 км, первый километр пробежал за 200 с. Каж-дый следующий километр он пробегал на t секунд дольше предыдущего. Найти t, если всю дистанцию бегун пробежал так, как если бы на каждый километр он затрачивал 202 с. (1 с)

1.62. В каком случае катер затратит меньше времени на то, чтобы проплыть одно и то же расстояние туда и обратно: по реке или по озеру? (По озеру)

1.63. Человек, идущий вниз по опускающемуся эскалатору, затрачивает на спуск 1 мин. Если человек будет идти вдвое быстрее, он затратит на 15 с меньше. Сколько времени он будет спускаться, стоя на эскалаторе? (1,5 мин)

1.64. *Автомобиль выехал из города А и приехал в город В. Первую половину времени движения автомобиль ехал со скоростью 40 км/ч, половину оставшегося расстояния он ехал со скоростью 60 км/ч, а остаток пути - со скоростью 80 км/ч. Найти среднюю скорость на всем пути. (≈ 54,3 км/ч)

1.65. *Автомобиль первую половину времени движения из одного города в другой ехал со скоростью 40 км/ч, а вторую половину времени - со скоростью 60 км/ч. С какой средней скоростью автомобиль проехал первую половину расстояния? ≈ 43 км/ч)

1.66. *Теплоход длиной 300 м плывет по озеру с постоянной скоростью. Катер, имею-щий скорость 90 км/ч, проплывает от кормы движущегося теплохода до его носа и сразу об-ратно за 37,5 с. Определить скорость теплохода. (15 м/с)

1.67. *Когда мимо пристани проплывает плот, от пристани в деревню, расположенную на расстоянии 15 км вниз по течению реки, отправляется моторная лодка. Она доходит до деревни за 45 мин и, сразу повернув обратно, встречает плот на расстоянии 9 км от деревни. Какова средняя скорость течения реки? (4 км/ч)

1.68. * Пункт В расположен на реке в 20 км ниже по течению от пункта А. Катер отправляется из А в В, затем сразу обратно в А и сразу опять в В. Одновременно с катером из А отплывает плот. При возвращении из В катер встретил плот в 4 км от пункта А. На каком расстоянии от А катер вновь догонит плот, следуя опять в В? (5 км)

1.69. *Из пункта А в пункт В одновременно вышли два пешехода. Когда первый прошел половину пути, второму осталось пройти 24 км, а когда второй прошел половину пути, первому осталось пройти 15 км. Найти расстояние АВ. (40 км)

1.70. *Велосипедист ехал из одного города в другой. Половину пути он проехал со ско-ростью 12 км/ч. Далее, половину оставшегося времени движения он ехал со скоростью 6 км/ч, а затем до конца шел пешком со скоростью 4 км/ч. Определить среднюю скорость велосипедиста на всем пути. (≈ 7 км/ч)

2. Механика жидкости

2.1. Сплав состоит из олова массой 2,92 кг и свинца массой 1,13 кг. Какова плотность сплава, если объем сплава равен сумме объемов его составных частей? (8100 кг/м3)

2.2. По свежему снегу прошел снегоход, масса которого с водителем 500 кг, а площадь опорной поверхности гусениц 0,75 м2. Со снегохода слез человек массой 80 кг и встал на след снегохода. Площадь одной подошвы валенок 250 см2. Будет ли человек проваливаться в снег? (Будет)

2.3. Объем медного шара 2000 см3, а его масса 6 кг. Определить, сплошной это шар или полый. Если полый, то определить объем полости. (Полый; 1320 см3)

2.4. Вес тела в воде в 6 раз меньше, чем в воздухе. Определить плотность тела. Вытал-кивающей силой воздуха пренебречь. (1200 кг/м3)

2.5. Кусок медного купороса весит в воздухе 100 мН, а в керосине 70 мН. Определить плотность медного купороса. (2700 кг/м3)

2.6. Вес куска железа в воде равен 68 Н. Определить его объем. (0,001 м3)

2.7. В воде тело весит 75 Н, а в керосине - 100 Н. Найти вес тела в глицерине. (43,75 Н)

2.8. Тело плавает в воде, погрузившись в нее на 0,75 своего объема. Найти плотность материала тела. (750 кг/м3)

2.9. Тело плавает в воде, погрузившись в нее на 0,75 своего объема. Какая часть объема тела будет погружена в спирт? (≈ 0,94)

2.10. В одной жидкости тело плавает, погрузившись в нее на половину, а в другой – на треть своего объема. Найти отношение плотностей этих жидкостей. (2/3)

2.11. Два тела: одно плотностью 1,5 г/см3 и объемом 0,5 cм3; другое - 0,5 г/см3 и 1,5 см3 связаны вместе и опущены в воду. Какая часть их общего объема погружена в воду? (0,75)

2.12. Кусок пробки массой 1,2 г привязан к куску железа массой 11,7 г. При погружении этих связанных тел в воду их вес оказался равен 0,064 Н. Определить плотность пробки. (240 кг/м3)

2.13. Колба из стекла вместимостью 1,5 л имеет массу 250 г. Какой минимальный груз надо положить в колбу, чтобы она утонула в воде? (1,25 кг)

2.14. Плоская льдина, плавая в реке, выступает из воды на 20 см. Какова толщина льди-ны? (2 м)

2.15. Определить наименьшую площадь плоской льдины толщиной 0,8 м, способной удержать на воде человека массой 100 кг. (1,25 м2)

2.16. Железный брусок массой 7,8 кг подвешен на нити и наполовину погружен в воду. Какова сила натяжения нити? (73 Н)

2.17. Мяч объемом 3 дм3 плавает в воде, погрузившись в нее на 1/5 своего объема. Какая масса воды должна попасть в мяч, чтобы он утонул? (2,4 кг)

2.18. Железный кубик плавает в ртути. Поверх ртути наливают воду. Какой толщины слой воды надо налить, чтобы она полностью покрыла кубик? Длина ребра кубика 10 см. Верхняя и нижняя грани кубика горизонтальны. (≈ 4,6 см)

2.19. Доска толщиной 5 см плавает в воде, погрузившись на 70% своего объема. Поверх воды разливается нефть толщиной 1 см. На сколько будет выступать доска над поверхностью нефти? (1,3 см)

2.20. Полый шар, отлитый из свинца, плавает в воде, погрузившись ровно наполовину. Найти объем внутренней полости шара, если масса шара 6 кг. (0,0115 м3)

2.21. Объем полости полого шара вдвое меньше объема шара. Опущенный в воду, шар погружается в нее на 0,75 своего объема. Найти плотность материала шара. (1500 кг/м3)

2.22. Полый медный шар плавает в воде во взвешенном состоянии. Чему равна масса шара, если объем воздушной полости равен 17,75 дм3? (≈ 20 кг)

2.23. Полый латунный шар с объемом полости 10 см3 плавает в керосине, погрузившись на ¾ своего полного объема. Определить массу шара. (≈ 6,45 г)

2.24. Кусок льда плавает в воде, погрузившись на 1/2 своего объема. Какую часть объема куска льда занимает воздушная полость в нем? Отношение плотностей льда и воды равно 0,9. (4/9)

2.25. Пустая пробирка, опущенная в воду, оказалась погруженной на 2/3 своего объема. После того как в нее положили дробинку массой 10 г, она оказалась погруженной на 3/4 объема. Найти массу пробирки. (80 г)

2.26. При погружении тела массой 1 кг в воду на половину его объема, вес тела умень-шается на 2 Н. Найти плотность тела. (2500 кг/м3)

2.27. Баржа представляет собой коробку размером 1042 м3. Ее масса с грузом 50 т. Можно ли погрузить в нее еще два контейнера по 20 т каждый? (Нет)

2.28. На поверхности воды плавает брусок, погруженный на 2/3 своего объема. Для того чтобы он затонул, на него необходимо положить гирю не менее 1 кг. Найти массу бруска. (2 кг)

2.29. При углублении дна реки грунт вывозят на барже в море. При переходе баржи из реки в море глубина ее осадки уменьшилась на 5 см, а при обратном переходе из моря в реку пустой баржи - увеличилась на 1 см. Определить массу вывезенного грунта, если площадь сечения баржи на уровне воды 1500 м2. Плотность морской воды 1030 кг/м3. (2060 т)

2.30. В сосуде находится вода массой 2 кг и кусок льда. В сосуд начинают вливать спирт при температуре 0 С, перемешивая содержимое сосуда. Сколько спирта надо влить, чтобы лед утонул? (1,6 кг)

2.31. Бревно длиной 3,5 м и поперечным сечением 0,04 м2 плавает в воде. Какую наибольшую массу может иметь человек, чтобы бревно не утонуло, когда человек встанет на него? Плотность дерева равна 500 кг/м3. (70 кг)

2.32. Человек стоит на плавающем бревне по пояс в воде. Какое минимальное количе-ство таких бревен он должен взять для плота, чтобы, стоя на нем, не замочить ног. Плотность тела человека практически равна плотности воды. (2)

2.33. В воде плавает плоская льдина площадью 2 м2. Когда на льдину встал человек массой 70 кг, высота верхнего края льдины над водой умень¬шилась в два раза. Какова толщина льдины? (0,7 м)

2.34. Два одинаковых по размеру шара с плотностью  и 2 связали нитью и опустили в воду. При этом один шар утонул, а второй погрузился на 0,8 своего объема. Определить . (600 кг/м3)

2.35. Полый медный шар весит в воздухе 17,8 Н, а в воде - 14,2 Н. Определить объем по-лости (1,6·10-4 м3)

2.36. Кастрюля емкостью 2 л доверху заполнена водой. В нее опускают плавать пустую банку объемом 1,5 л и массой 0,6 кг. Какая масса воды вытечет из кастрюли? (0,6 кг)

2.37. Шар, до половины погруженный в воду, лежит на дне сосуда и давит на его дно с силой, равной трети его силы тяжести. Найти плотность материала шара. (750 кг/м3)

2.38. Вес тела в воде в 2 раза меньше, чем в масле и в 3 раза меньше, чем в воздухе. Найти плотность масла. (500 кг/м3)

2.39. Из водоема с помощью веревки медленно вытаскивают алюминиевый цилиндр длиной 60 см и площадью поперечного сечения 100 см2. Когда над поверхностью воды ока-залась ¼ часть длины цилиндра, веревка оборвалась. Найти максимальную силу натяжения, которую выдерживает веревка. (117 Н)

2.40. Найдите подъемную силу воздушного шара объемом 20 м3, наполненного гелием, если масса оболочки шара с корзиной 12,4 кг. Плотность воздуха равна 1,3 кг/м3, а гелия - 0,2 кг/м3. (≈ 96 Н)

2.41. Шар объемом 1 м3, наполненный гелием, может удержать максимальный груз мас-сой 1 кг. Какой максимальный груз может удержать этот же шар, наполненный водородом? Плотности: гелия - 0,18 кг/м3, водорода - 0,09 кг/м3. (1,09 кг)

2.42. *Цилиндрическую гирю, подвешенную к динамометру, опускают в сосуд с водой. Когда уровень воды в сосуде изменился на 10 см, показание динамометра изменилось на 1 Н. Определить площадь сечения сосуда. (10 см2)

2.43. *Пластмассовый кубик плавает в некоторой жидкости, погрузившись в нее на треть своего объема. При погружении этого кубика в другую жидкость погруженный объем увеличивается вдвое. Какая часть кубика будет погружена, если смешать эти две жидкости в объемном отношении V1/V2 = 2 соответственно? (2/5)

2.44. *В цилиндрической банке высота уровня воды составляет 15 см. Когда в нее опу-стили плавать пустую латунную чашку, уровень воды поднялся на 2,1 см. Какова будет вы-сота уровня воды в банке, если чашку утопить? (15,25 см)

2.45. *Посередине большого озера просверлили прорубь. Толщина льда оказалась 8 м. Какой наименьшей длины веревку необходимо взять, чтобы зачерпнуть воду из проруби? (0,8 м)

2.46. *Кусок сплава меди и серебра весит в воздухе 2,94 H, а в воде - 2,65 Н. Сколько се-ребра и меди в куске? (≈ 0,211 кг; 0,082 кг)

3. Количество теплоты. Теплообмен

3.1. Определить температуру воды, установившуюся после смешения 39 л воды при 20 С и 21 л воды при 60 С. (34 °С)

3.2. Определить температуру воды, установившуюся после смешения 6 кг воды при 42 С, 4 кг воды при 72 С и 20 кг воды при 18 С. (30 °С)

3.3. Сколько литров воды при 95 С следует добавить к 30 л воды при 25 С, чтобы по-лучить воду при 67 С? (45 л)

3.4. Сколько литров воды при 20 С и 100 С нужно смешать, чтобы получить 300 лит-ров воды при 40 С? (225 л; 75 л)

3.5. Смешали 60 кг воды при 90 С и 150 кг воды при 23 С. 15% тепла было потеряно в окружающую среду. Определить конечную температуру воды. (40 °С)

3.6. Железную деталь, нагретую до 500 С, опускают в сосуд с водой, содержащий 18,6 л воды при 13 С. Какова масса детали, если вода нагрелась до 35 С? Испарением воды пренебречь. (8 кг)

3.7. Чугунный брусок массой 0,2 кг опускают в сосуд, содержащий 0,8 кг керосина при 15 С. Окончательная температура керосина - 20 С. Определить начальную температуру бруска. (98 °С)

3.8. В стеклянную колбу массой 50 г, где находилось 185 г воды при 20 С, вылили не-которое количество ртути при 100 С. Установилась температура 22 С. Определить массу ртути. (150 г)

3.9. Пластину массой 0,3 кг, нагретую до 85 С, опускают в алюминиевый калориметр массой 42 г, содержащий 0,25 кг воды при 22 С. Установившаяся температура 28 С. Опре-делить удельную теплоемкость вещества пластины. (382 Дж/кг·°С)

3.10. Сколько медных деталей, нагретых до 100 С и имеющих массу 1 кг каждая, можно охладить до температуры 30 С в сосуде, содержащем 100 л воды при 15 С? Удельная теп-лоемкость меди равна 376 Дж/кгград. (≈ 240)

3.11. Оловянный брусок массой 3 кг, нагретый до 230 °С, опускают в стальной сосуд с водой, имеющий температуру 15 °С. Установилась температура 35 °С. Определить массу во-ды в сосуде, если массы воды и сосуда равны, а потери тепла в окружающую среду состав-ляют 20%. (≈ 1,25 кг)

3.12. Нагретое до 100 С тело опустили в сосуд с водой и при этом температура воды повысилась с 20 С до 30 С. Какой станет температура воды, если в нее опустить еще одно такое же тело с температурой 50 С? (≈ 32,2 °С)

3.13. В батарею водяного отопления вода поступает при температуре 80 С по трубе се-чением 500 мм2 со скоростью 1,2 м/с, а выходит из батареи, имея температуру 25 С. Сколько тепла получает отапливаемое помещение в течение суток? (1,2·1010 Дж)

3.14. Для измерения температуры воды, имеющей массу 66 г, в нее погрузили термо-метр, который показал 32,4 С. Какова действительная температура воды, если теплоемкость термометра 1,9 Дж/град и перед погружением он показывал температуру 17,8 С? (32,5 °С)

3.15. Алхимик Петя изготовил 1 кг золотого порошка. Он достал его из печи, разогретой до температуры 1000 С, и ссыпал в кувшин с тремя литрами воды при 10 С. За этим из укрытия наблюдал злоумышленник Шура, которому для полного счастья не хватало грамм 200 золотишка. Петя вышел из комнаты и Шура, выскочив из укрытия, вытащил из кувшина горсть золота. Хватит ли Шуре украденного золота для счастья, если температура вытащен-ного золота была равна 70 С, а в кувшине установилась конечная температура 20 °С? (Хва-тит)

3.16. Имеются два одинаковых стакана, в первый налито 100 г воды, во второй - 100 г спирта при температуре 20 °С. В стаканы бросают два нагретых до 80 °С стальных шарика. После установления теплового равновесия температура воды составила 23 °С, спирта 24,5 °С. Вычислить теплоемкость стакана и массу шарика. (64,5 Дж/град; 55 г)

3.17. Две одинаковые кастрюли, содержащие одинаковые количества воды при одинаковой температуре одновременно поставили на две одинаковые плитки. Через некоторое время часть воды из первой кастрюли перелили во вторую, а спустя еще некоторое время такое же количество воды перелили обратно из второй кастрюли в первую. В какой кастрюле вода закипит быстрее? (В первой)

3.18. В чайник налили 1 л холодной воды и поставили на плиту. Когда через 10 мин вода закипела, в чайник добавили еще некоторое количество холодной воды. После этого вода вновь закипела через 3 мин. Сколько воды добавили? (300 г)

3.19. *Имеется два сосуда. В первом находится 5 кг воды при 60 С, а во втором - 2 кг воды при 20 С. Из первого сосуда во второй перелили некоторое количество воды. После установления равновесия из второго сосуда в первый перелили такое же количество воды. В результате в первом сосуде установилась температура 57 С. Какая температура установи-лась во втором сосуде? (27,5 °С)

3.20. *В чайник налили 1 л холодной воды при температуре 20 0С и поставили на плиту. Через 3 мин в чайник долили еще 1 л холодной воды. После этого вода закипела через 10 мин. Какая температура была в чайнике перед доливом? (≈ 57 °С)

3.21. *Имеется два сосуда. В одном налито 5 л воды при температуре 60 С, а в другом - 1 л воды при 20 С. Из первого сосуда во второй перелили некоторое количество воды. По-сле установления равновесия из второго сосуда в первый обратно перелили такое же количество воды. В результате в первом сосуде установилась температура 59 С. Какое количество воды переливали? (≈ 0,14 кг)

3.22. *В стакан, содержащий 200 г воды, опускают нагреватель мощностью 50 Вт. Мак-симальная температура воды после длительного нагревания составляет 55 С. За какое время вода в стакане остынет на 1 С после выключения нагревателя? (16,8 с)

3.23. *Некоторое количество воды нагревается электронагревателем мощностью 500 Вт. При включении нагревателя на время 2 мин температура воды повысилась на 1 С, а при его отключении - понизилась за 1 мин на ту же величину. Какова масса воды, если потери тепла в окружающую среду пропорциональны времени? (4,8 кг)

4. Фазовые превращения

4.1. В сосуд, содержащий 400 г воды при температуре 17 С, вводят 10 г пара при 100 С. Определить конечную температуру воды . (32 °С)

4.2. Алюминиевый калориметр массой 50 г содержит 250 г воды при температуре 16 С. Какое количество пара при 100 С следует ввести в калориметр, чтобы температура в нем повысилась до 90 С? (35 г)

4.3. В сосуд, содержащий 30 л воды, впускают 1,85 кг водяного пара при 100 С. После конденсации пара температура воды повысилась до 37 С. Найти начальную температуру воды. (0 °С)

4.4. Кусок алюминия массой 561 г, нагретый до 200 С, погрузили в 400 г воды при 16 С. При этом часть воды испарилась, а оставшаяся часть нагрелась до 50 С. Определить массу испарившейся воды. (7,4 г)

4.5. Через змеевик подогревателя, содержащего 12 л воды при 12 С, пропускают пар при 100 С. Вытекающая из змеевика вода имеет температуру 60 С. Какое количество пара нужно пропустить через змеевик, чтобы температура воды повысилась до 50 С? (≈ 0,78 кг)

4.6. В баке кипятильника с КПД 75% содержится 208 л воды при 15 С. Сколько пара при 104 С нужно пропустить через змеевик кипятильника, чтобы нагреть воду до 92 С? Температура воды, вытекающей из змеевика, тоже 92 С. (39 кг)

4.7. Пар поступает в змеевик нагревателя при 100 С, а из змеевика вытекает вода при 90 С. В течении часа через нагреватель прошло 2 м3 воды с начальной температурой 8 С, а из змеевика вытекло 360 л конденсата. До какой температуры нагрелась вода в нагревателе, если его КПД 80%? (88 °С)

4.8. В чайник налили воду при температуре 10 С и поставили на электроплиту. Через 10 минут вода закипела. Через какое время вода полностью выкипит? (61 мин)

4.9. На нагревание воды от 10 С до кипения на электроплите потребовалось 18 мин и еще 23 мин, чтобы обратить 20% воды в пар. Какова удельная теплота парообразования во-ды? (2,4·106 Дж/кг)

4.10. На нагреватель поставили открытый сосуд с водой. Через 40 мин после закипания воды в сосуд добавили массу воды, равную массе выкипевшей воды. Вода снова закипела через 3 мин. Найти начальную температуру добавленной воды. (60 °С)

4.11. В сосуде находится 2 кг льда и 10 кг воды. В сосуд подают водяной пар при темпе-ратуре 100 °С. Сколько воды окажется в сосуде в момент, когда ее температура станет равна 80 °С? (14 кг)

4.12. В два сосуда, содержащие по 300 г воды при температуре 80 С, опускают кипя-тильники. Мощность первого кипятильника вдвое больше мощности второго. Сколько воды выкипит в первом сосуде к моменту закипания воды во втором? (≈ 11 г)

4.13. Какое количество теплоты нужно затратить, чтобы 8 кг льда при 30 С расплавить и получившуюся жидкость нагреть до 60 С 2? (5,2·106 Дж)

4.14. В алюминиевый калориметр массой 0,2 кг, содержащий 0,34 кг воды при 23,5 C, опустил и 81,5 г льда при 0 С. Лед расплавился. Найти установившуюся температуру. (5,3 °С)

4.15. Какое максимальное количество льда можно положить в воду массой 1,5 кг при температуре 30 С, чтобы он весь растаял? Температура льда 0 С. Тепловых потерь нет. (≈ 573 г)

4.16. В латунном калориметре массой 125 г находится кусок льда массой 0,1 кг при тем-пературе −20 °С. Сколько воды при температуре 20 °С необходимо налить в калориметр, чтобы половина льда растаяла? Удельная теплоемкость латуни равна 380 Дж/кгград. (≈ 258 г)

4.17. В ведро с водой при 0 °С бросили кусочек льда. Через достаточно большое время выяснилось, что масса льда увеличилась на 2,1%. Определить начальную температуру ку-сочка льда. Теплообменом пренебречь. (−3,4 °С)

4.18. В калориметр, содержащий 0,4 кг воды при 17 С, брошено 0,05 кг мокрого снега. В результате температура воды в калориметре понизилась на 5 С. Сколько воды было в мокром снеге? Теплоемкость калориметра 160 Дж/град. (0,03 кг)

4.19. Смесь из 5 кг льда и 15 кг воды нужно нагреть до температуры 80 С, впуская в нее пар при 100 С. Определить необходимую массу пара. (≈ 3,5 кг)

4.20. В сосуд с водой с плавающими в ней льдинками при 0 С добавили 200 г воды при температуре 100 С. На сколько изменится масса льда в сосуде после того как температура станет опять равна 0 С? (≈ 255 г)

4.21. Какое минимальное количество водяного пара при 100 С необходимо израсходо-вать, чтобы растопить 1 кг льда при температуре 0 С? (≈ 121 г)

4.22. В смесь из 5 кг льда и 4 кг воды впустили 0,5 кг водяного пара при 100 С. Опреде-лить установившуюся температуру. Какая масса льда растает? (0 °С; ≈ 4,1 кг)

4.23. Сосуд с водой внесли в теплую комнату. При этом за 15 мин температура воды по-высилась на 4 С. За какое время в этой же комнате растает такое же количество льда при 0 С? Скорость теплообмена одинакова. (5 ч)

4.24. Домашний холодильник за 20 мин охлаждает 1,5 л воды от 16 С до 4 С. Сколько льда получится в холодильнике еще через час работы в этом же режиме? (0,6 кг)

4.25. За какое время можно обратить в 100 - градусный пар 1 кг снега при 10 С, если мощность электроплитки равна 2 кВт, а ее КПД 60%? (42,6 мин)

4.26. Для того чтобы растопить лед, довести образовавшуюся воду до кипения, а затем испарить ее, потребовалось 9 минут. Сколько времени таял лед? Скорость теплоподвода счи-тать постоянной. (≈ 58 с)

4.27. В сосуде находится лед. Для нагревания сосуда со льдом от 3 С до 1 С требует-ся некоторое количество теплоты. Для дальнейшего нагревания системы до 1 С требуется количество теплоты в 20 раз больше. Определить массу льда в сосуде. Теплоемкость сосуда равна 600 Дж/град. (≈ 90 г)

4.28. При изготовлении дроби расплавленный свинец при температуре плавления 327 С выливают в воду. Какое количество дроби изготовлено, если 3 л воды нагрелось при этом от 25 С до 47 С? Потери тепла составляют 25% 3. (6,3 кг)

4.29. В сосуд, содержащий 10 кг воды при 10 С, положили кусок льда при 50 С. В ре-зультате установилась температура 4 С. Какое количество льда положили? (41 кг)

4.30. На сколько температура воды у основания водопада больше чем наверху? Высота водопада 120 м. (0,28 °С)

4.31. С какой высоты должны свободно падать дождевые капли, чтобы при ударе о зем-лю испаряться? Начальная температура капель 20 С. Сопротивления воздуха нет. (265 км)

4.32. С какой скоростью должна лететь свинцовая пуля, чтобы расплавиться при ударе о стену? Температура летящей пули 20 С. Все тепло, выделяющееся при ударе, идет на плав-ление пули. (360 м/с)

4.33. Нагретая железная болванка массой 3,3 кг ставится на лёд, имеющий температуру 0 С. После охлаждения под болванкой расплавилось 460 г льда. Какова была температура болванки? (100 °С)

4.34. Нагретый железный кубик положили на лед, имеющий температуру 0 С. После остывания кубик погрузился в лед на 3/4 своего объема. До какой температуры был нагрет кубик? (≈ 62 °С)

4.35. В калориметре находится вода и лед при 0 С и в равных по массе количествах. За-тем туда доливают воду, масса которой равна массе содержимого калориметра, а температу-ра равна 49,9 С. Какая температура установится в калориметре? (≈ 5,3 °С)

4.36. Оловянный брусок массой 3 кг, нагретый до 230 С, опускают в стальной сосуд с водой, имеющий температуру 15 С. Установилась температура 35 С. Определить массу во-ды в сосуде, если массы воды и сосуда равны, а потери тепла в окружающую среду состав-ляют 20%. (≈ 1,25 кг)

4.37. В сосуд, содержащий 0,6 кг воды при 10 С, опускают 0,8 кг льда при 20 С. Определить установившеюся температуру и конечный состав содержимого сосуда. (t = 0 C; mв = 575 г; mл = 825 г)

4.38. В алюминиевый сосуд массой 100 г, содержащий 410 г воды при 24 С, опускают лёд при 0 С. Найти установившуюся температуру, если масса льда равна: а) 100 г; б) 150 г. (а) 4,7 °С; б) 0 °С)

4.39. В калориметре находится 300 г льда при 10 С. Туда кладут 250 г алюминия при 200 С. Какая температура установится? (0 °С)

4.40. В калориметр, где находится 1 кг льда при температуре 40 °С, впускают водяной пар массой 1 кг при температуре 120 °С. Определить установившуюся температуру. Удель-ная теплоемкость пара равна 2200 Дж/кгград. (100 °С)

4.41. В калориметре находится 400 г воды при 5 С. К ней долили еще 200 г воды при 10 С и положили 400 г льда при 0 С. Какая установится конечная температура? (0 °С)

4.42. Через охладитель компрессора за 1 час протекает 3250 кг воды, нагреваясь от 11 С до 17 С. Найти мощность двигателя, приводящего в действие компрессор, если его КПД равен 60%. (≈ 57 кВт)

4.43. В сосуд, содержащий 1 кг льда при 0 С, понемногу впускают водяной пар при 100 С. Сколько воды окажется в сосуде когда весь лед растает? (1,121 кг)

4.44. *В ведре находится смесь воды со льдом массой 10 кг. Ведро внесли в теплую комнату и сразу же начали измерять температуру. На рисунке представлена зависимость температуры содержимого ведра от времени. Определите по графику первоначальную массу льда в ведре. (1,23 кг)

4.45. *В сосуде находится смесь равных по массе количеств воды и льда. Через сосуд пропускают такое же количество по массе водяного пара при 100 С. Какая установится температура? Теплоемкостью сосуда и потерями тепла пренебречь. (100 °С)

4.46. *В 1 кг переохлажденной до 10 С воды бросили маленький кусочек льда, вызвав её замерзание. Сколько получится льда? До какой температуры надо переохладить воду, что-бы она вся превратилась в лёд? (125 г; −80 °С)

4.47. *При морозе 10 С каждый квадратный метр поверхности пруда отдает воздуху 180 кДж тепла в час. Какой толщины ледяной покров образуется за сутки, если температура воды 0 С? (1,2 см)

4.48. *В сосуде находится 100 г воды при 0 С. Выкачивая воздух из сосуда, воду замо-раживают посредством её испарения. Какая масса льда получится? (88 г)

4.49. *В куске льда, находящемся при температуре 0 С, сделано углубление объемом 160 см3. В это углубления налили 60 г воды при температуре 75 С. Каким будет незанятый водой объем углубления после установления равновесия? (≈ 106,3 см3)

4.50. *Имеется сосуд с отверстием у дна, в котором лежит кусок льда при температуре 0 С. Сверху на лед льется струя воды, температура которой 20 C, а массовый расход 1 г/c. Из отверстия в дне сосуда вытекает вода при температуре 3 C. Найти расход вытекающей воды. (≈ 1,2 г/с)

5. Теплота сгорания топлива. КПД двигателей

5.1. Какое количество керосина необходимо сжечь, чтобы 50 л воды нагреть от 20 С до кипения? КПД нагревателя 35%. (1,1 кг)

5.2. Определить КПД нагревателя, расходующего 80 г керосина на нагревание 3 л воды на 90 С. (33%)

5.3. Сколько времени потребуется, чтобы нагреть 1,55 л воды от 20 С до кипения, если горелка потребляет 0,3 кг спирта в час, а ее КПД 24%? (16 мин)

5.4. Пуля массой 9 г вылетает из ствола винтовки со скоростью 850 м/с. Масса порохо-вого заряда 4 г. Определить КПД выстрела. (27%)

5.5. Сколько тепла в сутки уходит из комнаты через окна и двери, если для поддержа-ния в ней постоянной температуры пришлось сжечь в печке 10 кг угля? КПД печки равен 35%. (105 МДж)

5.6. Найти КПД двигателя автобуса, расходующего 63 кг дизельного топлива за 2,5 часа работы при средней мощности 70 кВт. (23%)

5.7. Подвесной лодочный мотор "Вихрь" имеет мощность 13,2 кВт и КПД 15%. На сколько километров пути хватит ему 20 л бензина при скорости лодки 30 км/ч? (61 км)

5.8. Двигатель реактивного самолета с КПД 20% при полете со скоростью 1800 км/ч развивает силу тяги 88,2 кН. Определить расход керосина за 1 час полета и развиваемую мощность. (18,4 т; 4,41·104 кВт)

5.9. Сколько необходимо сжечь угля, чтобы 6000 кг воды взятой при 10 С нагреть до кипения и 1000 кг ее обратить в пар? КПД котла 70%. (215 кг)

5.10. Автомобиль совершает пробег длиной 120 км со средней скоростью 60 км/ч. На этом пути израсходовано 15 л бензина. КПД двигателя 30%. Какую среднюю мощность раз-вивает двигатель за время пробега? (≈ 20 кВт)

5.11. Вычислите КПД двигателя внутреннего сгорания, если известно, что развиваемая им мощность равна 100 кВт, а потребление бензина 50 л в час. Удельная теплота сгорания бензина равна 46106 Дж/кг, плотность бензина - 710 кг/м3. (≈ 22%)

5.12. Какое количество бензина потребуется для двигателя автомобиля, чтобы проехать 300 км, если масса машины 5 т, КПД двигателя 22%, а сопротивление движению составляет 0,05 от силы тяжести машины? Найти силу тяги двигателя и мощность, развиваемую при скорости 108 км/ч. (104 л; 2450 Н; 73,5 кВт)

5.13. Междугородный автобус проехал путь 80 км за 1 час. Двигатель при этом развивал среднюю мощность 70 кВт при КПД двигателя 25%. Сколько дизельного топлива, плотность которого 800 кг/м3, сэкономил водитель в рейсе, если норма расхода горючего - 40 л на 100 км пути? (2 л)

5.14. Двигатель, развивающий мощность 4200 Вт, имеет КПД 60%. Сколько литров воды в час надо пропускать через охлаждающую систему двигателя, чтобы она нагревалась не более чем на 5 °С? (480 л)

5.15. Какую массу нефти нужно сжечь на тепловой электростанции, чтобы по телевизору мощностью 250 Вт посмотреть фильм продолжительностью 1,5 часа? КПД электростанции 35%. Удельная теплота сгорания нефти 46106 Дж/кг. (84 г)

5.16. *Для того чтобы поддерживать в комнате температуру 20 oС при температуре на улице 10 oС приходится сжигать 0,1 м3 сухих дров в день. Сколько дров придется сжигать в день для поддержания в комнате той же самой температуры, если температура воздуха на улице опустится до 20 oC? (≈ 0,133 м3)

6. Электрический ток. Электрическое сопротивление

6.1. Что покажет гальванометр, если через него за 10 мин прошло 18 Кл электричества? (30 мА)

6.2. Сколько электронов за 1 с должно пройти через поперечное сечение проводника для того, чтобы включенный в цепь гальванометр показал 1 мА? Заряд электрона - 1,610-19 Кл. (6,2·1015)

6.3. Какое количество электричества проходит через поперечное сечение проводника за 10 с, если за этот промежуток времени ток равномерно возрастает от нуля до 6 А? (30 Кл)

6.4. По проводу протекает постоянный ток 10 А. Какая масса электронов протекает че-рез поперечное сечение проводника за год? Масса одного электрона равна 9,1110 31 кг. (1,8 г)

6.5. Каково удельное сопротивление провода, если его длина 10 км, площадь попереч-ного сечения 70 мм2, а сопротивление 3,5 Ом. (0,0245·10-6 Ом·м)

6.6. Металлическую полосу с сопротивлением 0,2 Ом разрезали вдоль длины на 3 оди-наковые части и соединили последовательно. Чему равно сопротивление полученного про-водника? (1,8 Ом)

6.7. Во сколько раз изменится сопротивление проводника, если его сложить пополам? Проводник не изолированный. (Уменьшится в 4 раза)

6.8. Прямоугольная пластина ABCD изготовлена из однородного проводящего материала, причем AC = 2AB (см. рис.). Если присоединить контакты к сторонам AB и CD, то сопротивление пластины равно 4 Ом. Каким будет сопротивление пластины, если присоединить контакты к сторонам AC и BD? (1 Ом)

6.9. Медный провод длиной 1 км имеет сопротивление 2,9 Ом. Найти массу провода. (≈ 52,7 кг)

6.10. Определить сопротивление нагревательного элемента, выполненного из константановой проволоки диаметром 0,8 мм и длиной 24,2 м. (≈ 24,1 Ом)

6.11. Какое количество меди следует израсходовать на электропровод длиной 5 км, что-бы его сопротивление было 5 Ом? (≈ 765,4 кг)

6.12. Два цилиндрических проводника имеют одинаковую длину и сделаны из одного материала. Но при этом сопротивление первого проводника вдвое меньше, чем второго. Ка-кой из проводников тяжелее и во сколько раз? (Первый вдвое тяжелей)

6.13. Резиновая трубка полностью заполнена ртутью. Во сколько раз изменится сопро-тивление трубки, если ее растянуть, увеличив ее длину в 1,5 раза? (Увеличится в 2,25 раз)

6.14. Найти отношение сопротивлений двух железных проволок одинаковой массы, если диаметр первой в два раза больше диаметра второй. (16)

7. Закон Ома. Параллельное и последовательное соединение проводников

7.1. Определить падение напряжения в линии электропередачи длиной 500 м при токе в ней 15 А. Проводка выполнена алюминиевым проводом сечением 14 мм2. (28,9 В)

7.2. При включении в электрическую цепь проводника длиной 4,5 м и диаметром 0,5 мм напряжение на его концах оказалось 1,2 В при токе 1 А. Определить удельное сопро-тивление материала провода. (5,3·10-8 Ом·м)

7.3. Напряжение на зажимах генератора 230 В. От генератора в электродвигатель по медным проводам сечением 10 мм2 на расстояние 350 м течет ток 15 А. Под каким напряже-нием работает двигатель? (212 В)

7.4. Электродвигатель, рассчитанный на напряжение 120 В и ток 20 А, установлен на расстоянии 150 м от источника напряжения 127 В. Определить нужное сечение проводов подводящей линии, если они медные. (≈ 14,7 мм2)

7.5. Электрическая лампа сопротивлением 430 Ом включена в сеть с напряжением 220 В. Сопротивление подводящих проводов 10 Ом. Определить падение напряжения на лампе и проводах. (215 В; 5 В)

7.6. Три потребителя электроэнергии сопротивлением 12 Ом, 9 Ом и 3 Ом, соединены последовательно. Напряжение на концах цепи 120 В. Найти ток в цепи и падение напряже-ния на каждом потребителе. (5 А; 60 В; 45 В; 15 В)

7.7. Цепь состоит из трех сопротивлений 10 Ом, 20 Ом и 30 Ом, соединенных последо-вательно. Падение напряжения на первом сопротивлении 20 В. Найти падение напряжения на остальных сопротивлениях и напряжение на концах цепи. (40 В; 60 В; 120 В)

7.8. Определить сопротивление реостата и лампочки, если наименьшее и наибольшее значение силы тока в цепи 1,5 А и 2,5 А (рис. 7.1). Напряжение на зажимах постоянно и рав-но 12 В. (3,2 Ом; 4,8 Ом)

7.9. В проводнике при напряжении 120 В был ток 1,5 А. Когда в цепь ввели дополнительное сопротивление, ток стал 1,2 А. Определить величину дополнительного сопротивления. Напряжение не менялось. (20 Ом)

7.10. В сеть c напряжением 220 В включены последовательно 10 ламп с сопротивлением по 24 Ом, рассчитанные на 12 В, каждая. Лишнее напряжение поглощается реостатом. Опре-делить силу тока в цепи и сопротивление реостата. (0,5 А; 200 Ом)

7.11. Какое сопротивление и как нужно подключить к проводнику с сопротивлением 24 Ом, чтобы получить сопротивление 20 Ом? (120 Ом; параллельно)

7.12. На сколько равных частей требуется разрезать проводник сопротивлением 64 Ом, чтобы, соединив их параллельно, получить сопротивление 1 Ом? (8)

7.13. Четыре проводника по 1,5 Ом каждый требуется соединить так, чтобы получить сопротивление 2 Ом. Как это сделать? (Три параллельно и один последовательно)

7.14. Общее сопротивление двух проводников при последовательном соединении 50 Ом, а при параллельном 12 Ом. Определить сопротивление каждого проводника. (20 Ом; 30 Ом)

7.15. Как изменится показание амперметра, если замкнуть ключ (рис. 7.2)? Лампочки одинаковые, напряжение постоянно. (Увеличится в 2 раза)

7.16. Два проводника 1 Ом и 5 Ом соединены параллельно. Определить ток в каждом проводнике, если общий ток 15 А. (12,5 А; 2,5 А)

7.17. Найти напряжение на сопротивлениях, если амперметр показывает 6 А (рис. 7.3). Номиналы сопротивлений даны в Омах. (18 В; 8 В; 8 В)

7.18. Определить сопротивление участка цепи, где R1 = 30 Ом, R2 = 60 Ом, R3 = 20 Ом, R4 = 40 Ом (рис. 7.4). (20 Ом)

7.19. Кусок проволоки сопротивлением 1,8 Ом согнули в виде равностороннего тре-угольника. Чему равно сопротивление полученного каркаса между двумя его вершинами? (0,4 Ом)

7.20. Определить общее сопротивление цепи (рис. 7.5), если R = 1 Ом. (2/3 Ом)

7.21. Найти общее сопротивление участка цепи АВ (рис. 7.6). В точке С электрического контакта нет. (0,4 Ом)

7.22. При замкнутом ключе сопротивление цепи между точками А и В (рис. 7.7) равно 80 Ом. Каким будет это сопротивление при разомкнутом ключе? (90 Ом)

7.23. Определить общее сопротивление цепи (рис. 7.8), если R1 = 3 Ом; R2 = 9 Ом; R3 = R4 = R6 = 6 Ом; R5 = 4 Ом. (3 Ом)

7.24. Определить общее сопротивление цепи (рис. 7.9), если R = 1 Ом. (1/3 Ом)

7.25. Однородный проволочный каркас в виде прямоугольника включается в цепь сначала точками А и В, затем точками В и С (рис. 7.10). Во втором случае сопротивление каркаса в 1,6 раза больше, чем в первом. Во сколько раз сторона ВС длиннее стороны АВ? (2)

7.26. Определить сопротивление R4 и показание амперметра А1, если R1 = 2,9 Ом, R2 = 1,8 Ом, R3 = 6 Ом, U = 12,4 В, а амперметр А показывает 2 А (рис. 7.11). (2 Ом; 1,5 А)

7.27. В представленной схеме (рис. 7.12) амперметр А1 показывает силу тока 2 А. Какую силу тока показывает амперметр А2? Сопротивления даны в Омах. (3,43 А)

7.28. *Найти показание идеального вольтметра в представленной схеме (рис. 7.13). R = 1 Ом, общее напряжение - 55 В. (5 В)

7.29. *Учитель предложил пятерым ученикам померить напряжения на пяти одинаковых сопротивлениях, собранных в представленную схему (рис. 7.14), с помощью пяти вольтметров. В результате получились такие результаты: U1 = 1 B; U2 = 1 B; U3 = 2 B; U4 = 4 B; U5 = 5 B. После этого учитель сказал, что у одного вольтметра была смещена шкала. Какое из напряжений измерили неправильно? (U¬4)

7.30. *Из куска проволоки сопротивлением 100 Ом сделали кольцо и в двух точках к этому кольцу подсоединили подводящие провода. В каком отношении точки подсоединения должны делить длину кольца, чтобы сопротивление между ними было равно 9 Ом? (1:9)

7.31. *В цепи, представленной на рис. 7.15, гальванометр показывает отсутствие тока. Выразить сопротивление Rx через R1, R2 и R3. ( )

7.32. *Во сколько раз изменится показание амперметра, если движок реостата передви-нуть из среднего положения в крайнее правое (рис. 7.16)? Общее напряжение не изменяется. (Увеличится в 3 раза)

7.33. *Если клеммы А и В (рис. 7.17) подключить к источнику с напряжением 10 В, а к клеммам С и D подключить вольтметр, то он покажет напряжение 8 В. Если к тому же ис-точнику подключить клеммы С и D, то на клеммах А и В напряжение равно 4 В. Найти зна-чения сопротивлений, если R1 + R2 + R3 = 22 Ом. (R1 = 2 Ом; R2 = 12 Ом; R3 = 8 Ом)

7.34. *В схеме, представленной на рис. 7.18, амперметр показывает 0,7 А. Что показыва-ет вольтметр? (0,2 В)

7.35. *Найти общее сопротивление участка цепи АВ (рис. 7.19). (R)

7.36. *В представленной на рис. 7.20 схеме амперметр А1 показывает 0,8 А. Что показы-вает амперметр А2. (0,1 А)

7.37. *Два конца графитового стержня, имеющего длину 50 см и площадь сечения 1 мм2, соединены с одним полюсом источника с напряжением 4,5 В. По стержню может переме-щаться контакт, соединенный через резистор с сопротивлением 3 Ом со вторым полюсом источника. Определить минимальное значение тока в резисторе. Удельное сопротивление графита равно 1,210-5 Омм. (1 А)

7.38. *Какой ток течет через амперметр в представленной на рис. 7.21 схеме? R1 = 15 Ом, R2 = R3 = R4 = 10 Ом, напряжение источника 7,5 В. (0,75 А)

7.39. *В представленной на рис. 7.22 цепи сопротивление между точками А и С равно 8 Ом, между точками В и D - 10 Ом, а между точками А и D – 9 Ом. Каково сопротивление между точками С и В? (9 Ом)

8. Тепловое действие тока

8.1. Амперметр и вольтметр, включенные в сеть, показывают 50 А и 120 В. Какая мощ-ность потребляется этими приборами, если сопротивление вольтметра 2500 Ом, а ампермет-ра 0,003 Ом? (7,5 Вт; 5,75 Вт)

8.2. Две электрические спирали имеют сопротивление 25 Ом и 20 Ом. Какое количе-ство теплоты выделится в этих спиралях, если их включить на 3 мин в сеть с напряжением 100 В при последовательном и параллельном соединении? (40 кДж; 160 кДж)

8.3. Какое количество тепла выделилось в реостате с сопротивлением 6 Ом, если за 5 мин через него прошло 600 Кл электричества? (7200 Дж)

8.4. В каком из четырех сопротивлений выделяется больше мощность? Сопротивления даны в Омах. (2 Ом)

8.5. Две плитки, рассчитанные на 250 Вт и 1000 Вт, соединили последовательно и включили в сеть. Найти отношение мощностей, потребляемых плитками. (4)

8.6. В сеть с напряжением 220 В последовательно включаются 2 лампы мощностью 60 Вт и 250 Вт, рассчитанные на напряжение 110 В каждая. Какая мощность будет выделяться в каждой лампе? (159 Вт; 39 Вт)

8.7. Сопротивления двух ламп, включенных параллельно в сеть с напряжением 120 В, относятся как 3 : 2. Определить выделяемые в лампах мощности, если сила тока в первой лампе равна 0,4 А. (48 Вт; 72 Вт)

8.8. Дуговая лампа включена последовательно с сопротивлением 7,3 Ом в сеть с напряжением 110 В. Потребляемая лампой мощность составляет 410 Вт. Определить ток в лампе и ее сопротивление в рабочем состоянии. (6,76 А и 9 Ом; 8,2 А и 6,1 Ом)

8.9. Мощность, потребляемая реостатом, 30 Вт, напряжение на его зажимах 15 В. Определить длину никелиновой проволоки, пошедшей на изготовление реостата, если пло-щадь ее сечения 0,5 мм2. (9 м)

8.10. Две лампы накаливания мощностью 100 Вт и 80 Вт рассчитаны на напряжение 120 В. Какую мощность будет потреблять каждая лампа, если их включить в сеть с этим напряжением последовательно? (19 Вт; 25 Вт)

8.11. Напряжение на зажимах генератора равно 132 В, а у потребителя - 127 В. Опреде-лить сопротивление подводящих проводов, если мощность, дошедшая до потребителя - 5 кВт. (0,13 Ом)

8.12. Генератор с напряжением на зажимах 220 В передаёт во внешнюю цепь мощность 11 кВт. Какого минимального сечения должны быть медные провода линии передачи длиной 50 м, чтобы потеря напряжения в них не превышала 2% от указанного напряжения? (19,5 мм2)

8.13. Сопротивление одной электрической лампочки 420 Ом. Какое количество ламп включено параллельно в цепь, если при напряжении 127 В мощность, потребляемая лампа-ми, равна 1,52 кВт? (40)

8.14. Сто одинаковых лампочек накаливания, соединенных параллельно, питаются от сети с напряжением 220 В. Сопротивление каждой лампочки равно 220 Ом. Определить по-требляемую мощность. (22 кВт)

8.15. Электрический двигатель, обмотка которого имеет сопротивление 2,2 Ом, работает от источника электрической энергии с напряжением 120 В при токе 7,5 А. Определить поте-рю мощности в обмотке двигателя и его КПД. (124 Вт; 86%)

8.16. На сколько градусов изменится температура воды в калориметре, если через нагре-ватель пройдет 300 Кл электричества? Напряжение на нагревателе 210 В, масса воды 5 кг, теплопотерями пренебречь. (3 °С)

8.17. Два проводника с сопротивлением 5 Ом и 7 Ом соединяют параллельно и подклю-чают к источнику. В первом проводнике выделилось 1 кДж тепла. Какое количество тепла выделилось во втором проводнике за то же время? (714 Дж)

8.18. Сколько времени длится нагревание 3 л воды от 18 С до кипения в электрическом чайнике мощностью 800 Вт с КПД 87%? (24,7 мин)

8.19. Электрический кипятильник нагревает за 5 мин 210 г воды от 14 С до кипения. Определить сопротивление кипятильника, если он работает от сети с напряжением 120 В. (57 Ом)

8.20. Электрический кипятильник мощностью 1 кВт, работающий от сети с напряжени-ем 220 В, за 12 мин нагревает 1,5 л воды на 88 градусов. Определить величину тока в цепи и КПД нагревателя. (4,4 А; 77%)

8.21. Какой длины надо взять нихромовую проволоку сечением 0,1 мм2 для нагревателя, на котором можно за 5 мин довести до кипения 1,5 л воды, взятой при температуре 20 0С. Напряжение в сети 220 В, КПД нагревателя 90%. (2,36 м)

8.22. Электрический нагреватель мощностью 0,8 кВт и с КПД 50% содержит 0,6 л воды при температуре 8 0С. Через 10 мин после включения в него долили 0,3 л воды с температу-рой 8 °С. Определить установившуюся температуру. (≈ 69,2 °С)

8.23. Какую площадь поперечного сечения должна иметь свинцовая проволока предо-хранителя, чтобы при прохождении через него тока 1 А перегорание предохранителя проис-ходило через 1 с? Начальная температура проволоки равна 20 С, температура плавления свинца 327 С. (0,0215 мм2)

8.24. Сколько льда при температуре 10 °С можно растопить за 10 мин на электрической плитке, работающей от сети с напряжением 220 В при токе 3 А, если КПД плитки 80%? (0,9 кг)

8.25. Имеются три электрические лампы, рассчитанные на напряжение 110 В каждая. Мощности ламп равны 50 Вт; 50 Вт и 100 Вт. Как надо включить эти лампы в сеть с напря-жением 220 В, чтобы они давали нормальный накал? (Две первые параллельно, третья по-следовательно)

8.26. В сеть с напряжением 120 В параллельно включены две лампы (см. рис.). Лампа 1 имеет мощность 300 Вт и рассчитана на напряжение 120 В. Лампа 2 рассчитана на напряжение 12 В и включена последовательно с резистором так, что работает в расчетном режиме. Определить показания амперметров А1 и А и сопротивление резистора, если показание амперметра А2 равно 2 А. (2,5 А; 4,5 А; 54 Ом)

8.27. Электрический аппарат для перегонки воды потребляет от сети мощность 2,5 кВт. Сколько дистиллированной воды получают при помощи этого аппарата в течение 1 ч, если его КПД 80%, а вода поступает из водопровода при температуре 10 С? (2,68 кг)

8.28. Электрический чайник, содержащий 600 г воды при 9 С и имеющий сопротивле-ние обмотки 16 Ом, включили в сеть с напряжением 120 В и забыли выключить. Через какое время вся вода выкипит, если КПД чайника 60%? (49 мин)

8.29. В представленной схеме вольтметр показывает напряжение 10 В. Какое количество теплоты выделится в сопротивлении 2 Ом за 3 мин? (12,96 кДж)

8.30. Две лампочки имеют мощности 60 Вт и 100 Вт и рассчитаны на одинаковое напряжение. Лампочки соединили последовательно и включили в сеть с таким напряжением, что на первой лампочке выделяется ее номинальная мощность 60 Вт. Какая мощность при этом выделяется на второй лампочке? (36 Вт)

8.31. Электропоезд при движении со скоростью 54 км/ч потребляет мощность 9000 кВт. КПД электродвигателя 80%. Определить силу тяги, развиваемую двигателем. (480 Н)

8.32. Три лампочки мощностью N1 = 50 Вт, N2 = 25 Вт и N3 = 50 Вт, рассчитанные на напряжение 110 В каждая, соединены, как показано на рисунке, и включены в сеть с напря-жением 220 В. Какая мощность выделяется в каждой лампочке? (72 Вт; 16 Вт; 32 Вт)

8.33. *Медная и свинцовая проволоки одинакового сечения соединены последовательно и подключены к источнику напряжения. На сколько градусов нагреется медная проволока к тому моменту, когда свинцовая начнет плавиться, если начальная температура проволок 20 0С, а температура плавления свинца 327 °С? (≈ 11 °С)

8.34. *Электрическая кастрюля и чайник, потребляющие мощность 600 Вт и 300 Вт со-ответственно, включены в сеть параллельно и вода в них закипает одновременно через 20 мин. Через какое время закипит вода в кастрюле и чайнике, если их включить в сеть после-довательно? (180 мин; 45 мин)

8.35. *Проволока, подключенная к источнику напряжения, начинает плавиться через 2 с после подключения. Через какое время начнет плавиться проволока из того же материала, все линейные размеры которой (длина и диаметр) втрое больше? Напряжение постоянно. Теплообменом с окружающим воздухом пренебречь. (18 с)

8.36. *В комнате горит елочная гирлянда из двадцати одинаковых лампочек, соединен-ных последовательно, мощностью 0,25 Вт каждая. Одна из лампочек перегорела, и ее заме-нили другой, рассчитанной на то же напряжение, но мощностью 0,75 Вт. Будет ли в комнате светлее? (Будет)

8.37. *Четыре проводника, сопротивление которых 1 Ом; 2 Ом; 3 Ом и 4 Ом соединены так, что общее сопротивление оказалось равным 1 Ом. Какая мощность выделяется в про-воднике 2 Ом, если ток в проводнике 3 Ом равен 3 А? (72 Вт)

8.38. *Чему равно сопротивление подводящих проводов, если два одинаковых чайника при напряжении 220 В закипают за одно и то же время при последовательном и параллель-ном включениях? Потребляемая каждым чайником мощность при этом равна 400 Вт. (13,4 Ом)

8.39. *Электрический утюг, рассчитанный на напряжение 120 В, имеет мощность 300 Вт. При включении утюга в розетку напряжение в ней падает от 127 В до 115 В. Определить сопротивление проводов, подводящих напряжение к розетке. (5 Ом)

8.40. *Электрический чайник закипает за 24 мин. Как надо разделить его обмотку на 2 секции, чтобы при включении одной из них чайник закипал за 8 мин? За какое время закипит чайник, если включить одну вторую секцию? За какое время закипит чайник, если включить обе секции параллельно? (R1 = R/3; R2 = 2R/3; 16 мин; 5,33 мин)

8.41. *Лифт массой 1,5 т поднимается на высоту 20 м за 40 с. Напряжение на зажимах электродвигателя 220 В, его КПД 85%. Определить силу тока в двигателе и сопротивление его обмоток. (≈ 40 А; ≈ 0,81 Ом)

8.42. *Два сопротивления R1 = 1 кОм и R2 = 5 кОм, рассчитанные на максимальную мощность по 2 Вт каждое, соединили последовательно. Какую максимальную мощность можно получить от такой схемы? (2,4 Вт)