Եռանկյունաչափությունը կյանքում

Тригонометрия в строителстве

Пример

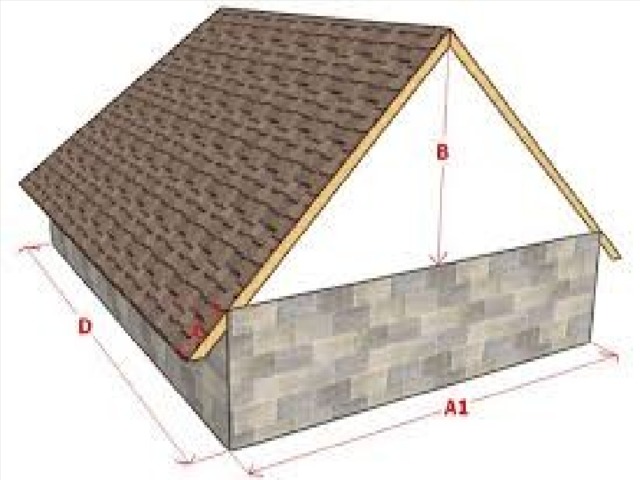
• Строим двускатную крышу. Угол ската 40 градусов. Ширина половини крыши 5 метров. Какой длини стропила нужны? Угол наклона необходимо точно рассчитать. Несоблюдение заданных параметров приводит к негативным последствиям. Таким образом , правильный уклон обеспечит двускатной крыше долговечность и безопасность. Основанием для расчета зтого покозателя служат соответствующие таблици ветровой нагрузки для того или иного региона.
• Стропила это гипотенуза нашего треугольника. Известен катет b=5метров и угол 40 градусов. Тогда используя формулу
• b=Ccosα, найдем гипотенузу C. Cos40 =0,766
• C=6,53 и с помощю тангенса найдем высоту центральной стойки. Как видим , тригонометрия может облегчить жизнь во время стройки.

40

40

5

5м

Тригонометрия в медицине

Аппараты ЭКГ снимают кардиограмму у людей, фиксируя удары сердца. Этот расчет необходим для оценки частоты ритма, где форма и величина зубцов в разных отведениях будет показателем характера ритма, происходящих электрических явления в сердце и электрической активности отдельных участков миокарда, то есть, электрокардиограмма показывает, как работает наше сердце в тот или иной период.

График электрокардиограммы является измененной синусоидой. И здесь важна каждая неровность графика. Количество интервалов и зубцов, максимум и минимум скачков, протяженность периодов: все это играет важную роль в определении диагноза и правильности лечения. При расшифровке результатов ЭКГ проводят измерение продолжительности интервалов между ее составляющими.

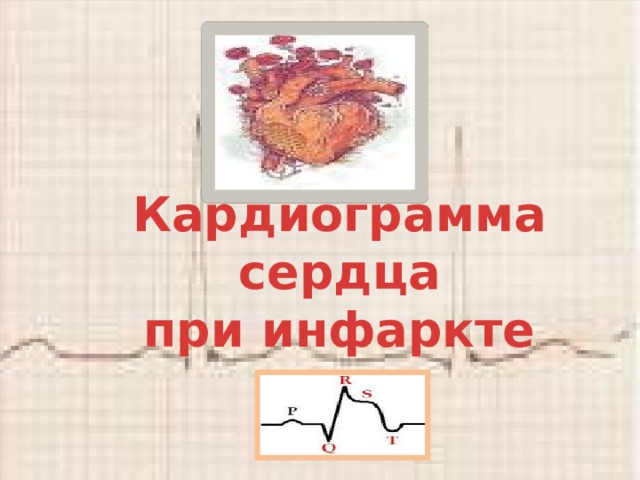
Кардиограмма сердца

при инфаркте

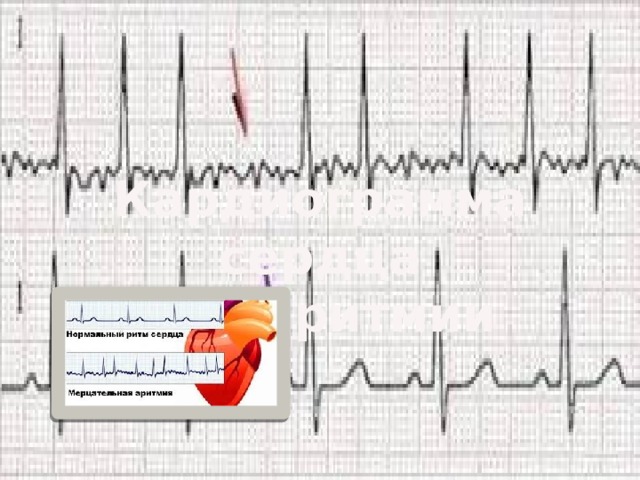
Кардиограмма сердца

при аритмии

Тригонометрия в биологии

• Все живые существа на Земле - от растений до высших млекопитающих - подчиняются суточным ритмам. У человека в зависимости от времени суток циклически меняются физиологическое состояние, интеллектуальные возможности и даже настроение. это периодические изменения интенсивности и характера биологических процессов поддерживаются и воспроизводятся в любых условиях. У каждого организма есть свои циклы, которые помогают ему чередовать фазы активности и восстановления. это колебания интенсивности различных биологических процессов в организме, связанные со сменой дня и ночи, описывается при помощи  тригонометрических функций .

Тригонометрия в

астрономии

и физике

Существует множество областей , в которых применяются тригонометрия.

Например, метод триангуляции используетсяв астрономии для измерения

расстояния до ближайших звезд, в спутниковых навигационных системах.

Синус и косинус имеют фундаментальное значение для теории пероидечис-ких функций, например при описании звуковых и световых волн. Тригонометрия используется в астрономии (особенно для расчетов положения небесных обьектов , когда требуется сферическая тригоно-метрия). В окружающем нас мире приходится сталкиваться с периодическими процессами , которие повторяются через одинаковые промежутки времени . Эти процессиы называются колебательными .

Колебательные явления рарличной физической природи подчиняются общим закономерностям и опысиваются одинаковыми уравнениями.

Существуют разние види колебательных явлений.

Гармоническое колебание явление периодического изменения какой –либо величины, при котором зависимость от аргумента имеет характер функции синуса и косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом.

x(t) = Acos(ωt+ ϕ) y(t) = Asin(ωt+ ϕ)