Звездный час (внеклассное мероприятие по математике в 8 классе)

Городской отдел образования г. Шымкента

Общеобразовательная средняя школа №39 имени М.Жумабаева

Методическая разработка внеклассного мероприятия

в 8-х классах

«Звездный час»

Подготовили: учителя математики

Славкина Н.В., Алимжанова Г.Н.

г. Шымкент, 2022-2023 учебный год

Методическая разработка внеклассного мероприятия «Звездный час»

Предмет: математика.

Целевая аудитория: учащиеся 8г, 8д и 8е классов

Цели проведения:

Образовательные:

- Научить применять теоретические знания и практические умения и навыки, полученные на уроках математики при решении квадратных уравнений и задач, связанных с ними.

- Способствовать формированию интереса к урокам математики.

- Совершенствовать навыки работы в группе, планирования ответа и монологической речи.

Воспитательные:

- Совершенствовать навыки коллективной работы.

- Способствовать развитию логического мышления, речи, памяти, внимания.

- Показать ценность каждого члена коллектива как личности.

- Создать ситуацию, в которой необходимо проявить умение брать инициативу на себя, принимать ответственные решения.

- Учить стойкости, собранности, терпимости.

Задачи развития интеллекта, воли, эмоций, познавательного интереса и способностей:

- Развивать умения анализировать ситуацию, выделять главное, сопоставлять факты, выбирать наиболее вероятные ответы.

- Развивать ассоциативное мышление.

- Воспитывать эмоциональную устойчивость в экстремальных ситуациях, дать практику преодоления трудностей.

- Развивать познавательный интерес.

Оформление: три стола для команд участников, портреты ученых- математиков, интерактивная доска или проектор с экраном, презентация.

Сценарий математического конкурса «Звездный час» для учеников 8-х классов

Учитель: Добрый день, дорогие друзья! Сегодня вместе мы с вами проведем мероприятие, которое мы условно назвали «Звездный час». Почему именно так? Я думаю, что на этот вопрос мы ответим в конце встречи вместе. (Слайд 1)

Ведущий 1: Наверное, вам известно, что слово “математика” пришло к нам из древнегреческого языка. По-древнегречески “мантанейн” означает “учиться”, “приобретать знания”. Много тысяч лет люди накапливали математические знания, т.е. знания о числах, количествах и количественных отношениях. Без таких знаний древние египтяне, например, не смогли бы построить свои знаменитые пирамиды, а в древней Индии не изобрели всемирно известные ныне шахматы.

Ведущий 2: Математика помогает нам познавать и совершенствовать тот мир, в котором мы живем. Запуск на орбиту спутников, строительство автострад, вождение поездов, даже оклейка стен обоями, - все это и многое другое было бы просто невозможно без математических расчетов. Математика помогает нам учиться мыслить яснее и последовательнее. (отрывок из поэмы Н. И. Кованцева на фоне Слайд 2)

Ведущий 1: Преданье старинное знает весь свет,
  Как тешась горячею ванной,
  Открыл свой великий закон Архимед,
  Связав его с выходкой странной . . .

Ведущий 2: Сияющий выскочил вон Архимед
  Из ванны горячей, где мылся,
  И прямо из бани, как был не одет,
  Куда – то бежать он пустился . . .

  Ведущий 1: Картина, достойная кисти богов:
    По улице, солнцем нагретой,
    Пунктир оставляя из мокрых следов,
    Бежит Архимед неодетый.

Ведущий 2: Толпа сиракузцев несётся вослед,
    В восторге от бешеной гонки,
    И громко ликует, когда Архимед
    Выкрикивал “Эврика!” звонко.

Ведущий 1: Нашёл! Он нашёл тот желанный ответ,
    Который искал так упорно!
  “Нашёл!” - в упоеньи кричал Архимед,
  “Нашёл!” - повторяли задорно . . .

Ведущий 2: Да, действительно, великое открытие совершил Архимед, и поэтому его слово «эврика» стало как призыв. И я хочу, чтобы каждый из вас совершил свое открытие нового (пусть уже кем-то открытого) для себя и также мог воскликнуть громко: «Эврика!» и предлагаю девизом конкурса сделать именно это слово и поэтому прошу: давайте все вместе воскликнем также с озарением: ЭВРИКА!!! (Слайд 3)

Ведущий 1: Итак, начинаем дорогу к своему звездному часу, которая будет состоять из нескольких этапов. А для начала представим членов жюри, которые помогут определить, чья команда будет сегодня успешнее и достигнет своего звездного часа. (представление членов жюри)

Ведущий 1: А теперь давайте выясним, кому из вас будет предоставлено право проложить свою дорогу к славе.

Этап 1 – «Отборочный» (зрительному залу задаются вопросы, учащиеся, первыми ответившие верно, вызываются на сцену) (Слайд 4)

Вопросы отборочного тура:

Задание 1. Два путешественника одновременно подошли к реке. У берега привязана лодка, в которой может переправиться только один человек. Путешественники не умели плавать, но каждому из них удалось переправиться через реку. Внимание вопрос: как могло это произойти? (Они подошли с разных сторон.) 

Задание 2. Существует легенда о греческом изобретатели  Дедале (мастере, сделавшем крылья Икару) и его племяннике, очень талантливейшем юноше, который придумал гончарный круг, первую в мире пилу и то, что лежит в этом ящике. За это молодой человек поплатился жизнью, так как завистливый дядя столкнул его с высокого городского вала. Самый древнейший такой предмет пролежал в земле почти 3000 лет. В нашей стране впервые был обнаружен на раскопках в Нижнем Новгороде. В Древней Греции умение пользоваться этим предметом считалось верхом учёности, а умение решать задачи с его помощью – признаком большого ума. О чем идет речь? (О циркуле)

Задание 3. Однажды в магазине мальчики купили 6 перьев, несколько тетрадей по 3 рубля и 3 карандаша. Продавец выписал чек на 40р. 40к. – вы ошиблись, - сказал ему мальчик, как только взглянул на чек, продавец был удивлен, как мальчик, не подсчитав денег, заметил ошибку. Проверка показала, что мальчик был прав. Скажите, как мальчик догадался? (Сумма должна быть кратна 3.)

Задание 4. Перед вами игральная карта - бубновый туз. Посмотрите внимательно: на карте вы видите изображение ромба. Почему на карте бубновой масти изображен именно  ромб, а не что-нибудь другое? («Ромб»- бубен, а раньше бубны имели форму ромба или квадрата)

Задание 5. Вам  наверное знакома басня И. А. Крылова «Волк и ягненок». Автор утверждает: « У сильного всегда бессильный виноват: тому в истории мы тьму примеров слышим». Какое число встречается в этих строках и как оно переводилось у народов?  (Тьма - очень много, десять тысяч, сотня сотен.)

Задание 6. Летели утки: одна впереди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Сколько летело уток? (Три утки: одна за другой.)

Задание 7. Пять десятков умножили на пять десятков. Сколько получилось десятков? (250 десятков.)

Задание 8. Эту теорему изучают в средней школе. Во Франции в средние века называли «мостом ослов», у математиков арабского Востока эта теорема получила название «теорема невесты». Как формулируется эта теорема?(Теорема Пифагора.)

Задание 9. Голландский математик 16в. Симон Стевин писал: «При одном их виде учащиеся приходят в такое уныние, что останавливаются и восклицают: ради Бога, не надо дальше!» Про какие числа писал Симон Стевин? (Обыкновенные дроби.) 

Задание 10. Современные цифры 1,2,3,4,…,9 ценнейший вклад в математических знаниях. Очень скоро эти цифры заимствовали арабы, от них они в 10-13в.в. распространились в Европе, а затем во всем мире. У народов какой страны эти цифры позаимствовали арабы? (У индусов, Индия.)

Задание 11. Точка, от которой в Венгрии отсчитывают расстояние, отмечена особо. В этом месте в центре Будапешта поставлен памятник. Кто удостоился таких почестей? (Нуль)

Задание 12. Эта старинная мера обозначает расстояние от 19 до 23 см. т.е. расстояние между двумя вытянутыми пальцами большим и указательным. Название этой меры сохранилось в пословице, когда говорят об очень умном человеке. Как называется мера. (Пядь. Семь пядей во лбу).

Задание 13. От трудов этого ученого шли все замыслы дальнейшего, более совершенного обоснования геометрии. Ему принадлежат слова: «В математике нет царской дороги». Назовите имя учёного. (Евклид).

Задание 14. Улитка ползает по столбу высотой 10 м. за день она поднимается на 5 м, а за ночь опускается на 4 м, за какое время улитка доберется от подножия до вершины столба? (5,5 суток)

Задание 15. Как из 13 спичек получить сто? Ломать спички запрещено! (составить из спичек число «100» или слово «сто»)

Задание 16. В музыке существуют миллионы аккордов. В математике существуют миллионы чисел. Но без этого числа математика — не более чем арифметика. Без этого аккорда музыка — не более чем шум. (число ноль, пустой аккорд)

Задание 17. В математике известны различные способы записи цифр, но в современном мире наиболее применимы арабские цифры. Какие цифры не получили широкого применения из-за невозможности выполнения с ними умножения и деления в столбик? (римские)

Задание 18. Главная героиня фильма «Снежное чувство Миллы» говорит, что ОНА — это огромный, безграничный пейзаж: ты идешь к горизонту, который всегда отступает. Как Гренландия. О чем идет речь? (математика)

Задание 19. Самое сказочное число (три)

Задание 20. Галилео Галилей говорил, что на ее языке написана книга природы (язык математики)

Задание 21. Что Песталоцци считал основой порядка в голове? (счет и вычисления)

Задание 22. Химия – правая рука физики, а что является ее глазами? (математика)

Задание 23. Что тяжелее килограмм железа или килограмм пуха? (они весят одинаково)

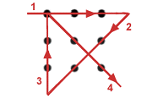
Задание 24. Соедините 9 точек четырьмя прямыми линиями не отрывая руки и не обводя линий.
( )

Задание 25. Исправьте ошибку в числовом равенстве XIV - V = XX . Передвинуть можно только одну спичку! (XV + V = XX)

Задание 26. Кирпич весит 1 килограмм плюс половину собственного веса. Сколько весит кирпич? (2кг)

Задание 27. 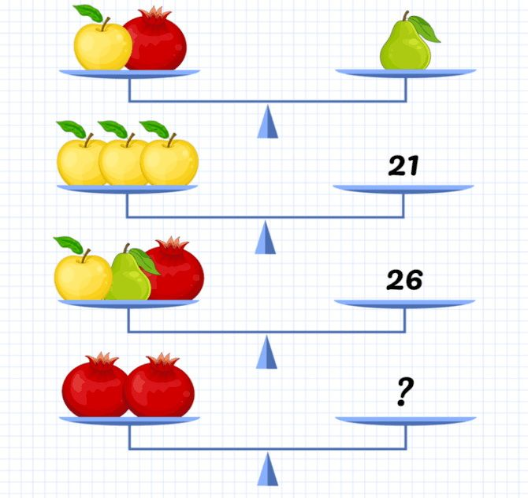? (12)

Задание 28. Вы бросили мяч, и он прилетел к Вам назад, ни обо что не ударившись на своём пути и не попав к кому-либо в руки. Как вам это удалось? (мяч был брошен вертикально вверх)

Задание 29. На ветке сидели три птички, две из них решили полетать. Сколько птичек сидит на ветке? (3, ни одна из них еще не улетела)

Задание 30. Что не может увеличить лупа в фигуре? (углы)

(учащиеся на сцене делятся на три команды и садятся за столы)

Этап 2 – «Разминка» (каждая команда получает листок с уравнениями, решает их и сдает жюри, команде, сдавшей задания первой, начисляется 2 дополнительных балла; команде, сдавшей задания второй, 1 дополнительный балл ) (карточки, слайд 5 с названием тура «Байга»)

Этап 3 – «Путешествие в прошлое» (Слайд 6)

Ведущий 1: Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведенных над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучаются общие свойства действий над величинами.

Ведущий 2: Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне.

Ведущий 1: Задачи на квадратные уравнения встречаются и в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме.

Ведущий 2: В алгебраическом трактате великого ученого древнего востока Аль-Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, куда вошли как полные, так и неполные квадратные уравнения.

Ведущий 1: Сегодня вы побываете в роли древних ученых и используя современные методы решения квадратных уравнений, попробуете решить их задачи.

(капитаны команд выходят и берут со стола жюри лист с задачей, который перевернут текстом вниз, задача команд обсудить задачу, решить ее и презентовать присутствующим в зале)

« Обезьянок резвых стая

Всласть поевши, развлекалась

Их в квадрате часть восьмая

На поляне забавлялась

А двенадцать по лианам

Стали прыгать, повисая

Сколько ж было обезьянок,

Ты скажи мне, в этой стае?»

Квадрат и число 21 равны 10 корням. Найти корень.

Пока команды обсуждают свои решения ведущие проводят игру со зрителями:

1. Что отличает один поезд от другого с точки зрения математики? (Номер поезда).

2. Без чего не могут обойтись охотники, барабанщики и математики? (Без дроби).

3. Что есть у каждого слова, растения и уравнения? (Корень).

4. Какая геометрическая фигура используется для наказания детей? (Угол).

5. Какая геометрическая фигура дружит с солнцем? (Луч).

6. Какая дуга вошла в историю ХХ – го века? (Курская дуга).

7. Как было названо военно-историческое кольцо? (Блокада).

8. Многогранник из Египта. (Пирамида).

9. Географический конус? (Вулкан).

10. Угол на который поворачивается солдат кругом (180)

(за каждый верный ответ зритель получает звезду)

По завершении решения задач команды выбирают представителя для презентации.

Этап 4 «Конкурс капитанов» (капитанам каждой из команд выдается лист с сеткой, заполненной буквами, их задач, двигаясь только по прямым линиям, найти как можно больше математических названий) (Слайд 8)

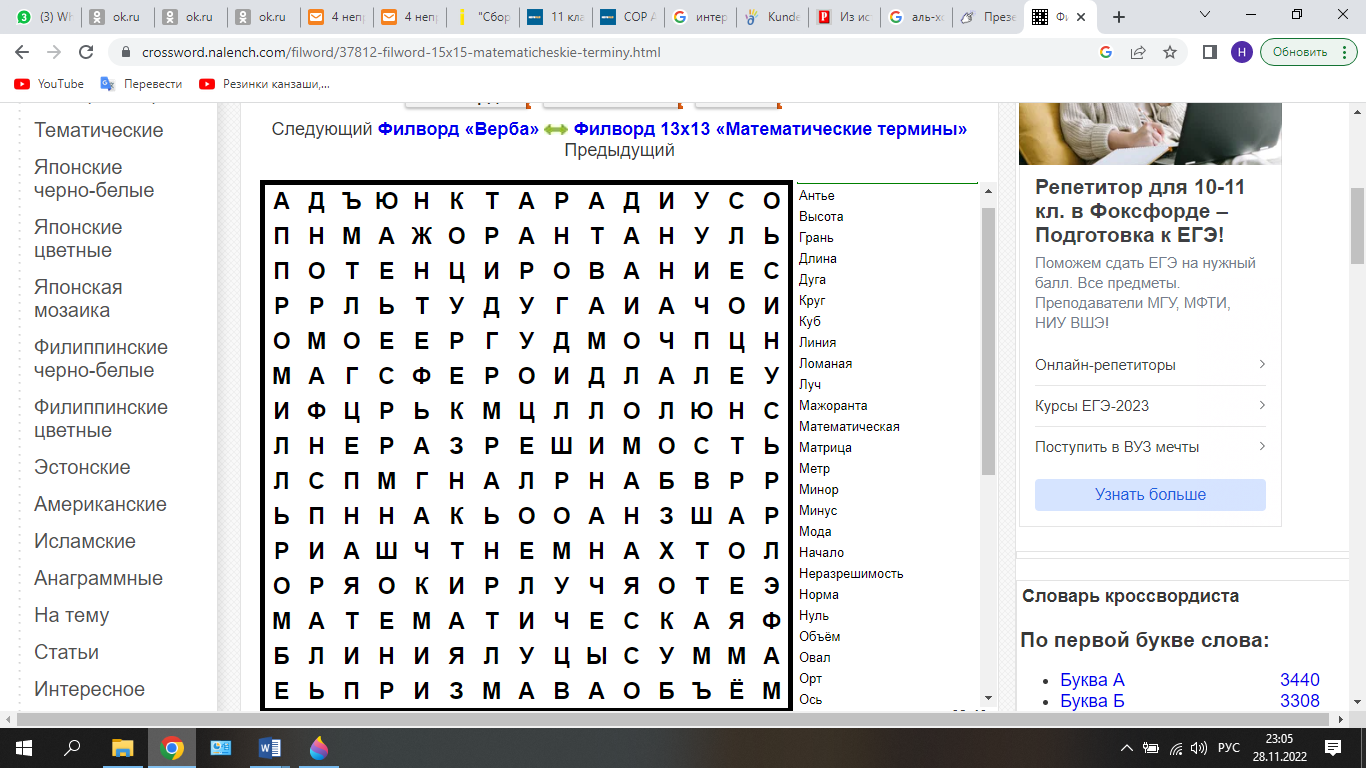
На выполнение задания дается 10 минут. По завершении капитаны по очереди называют найденные термины (те, что были уже озвучены не засчитываются). Побеждает та команда, которая назовет последний термин.

Этап 5 «Поддержка зрителей» (пока капитаны готовятся ведущие проводят игру со зрителями «Ребусы»)

Число Степень Знаменатель Ответ Периметр Точка

Задача Угол

(Слайды 11-18)

(за каждый верный ответ зритель получает звезду)

Эап 6 «Домашнее задание» (команды получили домашнее задание найти дополнительные способы решения квадратных уравнений и презентовать их в произвольной форме)

Ведущий 1: А теперь дадим жюри время для подведения итогов.

Ведущий 2: А пока мы попытаемся доказать всем присутствующим то, что в школе вы проводите не так уж и много времени.

Ведущий 1: Все вы наверное считаете, что школа отнимает у вас много времени. А хотите мы докажем, что в течение целого года вы практически не бываете в школе. В году 365 дней.

Ведущий 2: Из них 52 воскресенья и, по крайне мере, 10 других дней отдыха, поэтому отпадает 62 дня.

Ведущий 1: Летние и зимние каникулы продолжаются не менее 100 дней. Следовательно, уже 162 дня.

Ведущий 2: Ночью в школу не ходят, а ночи составляют половину года, следовательно, ещё 182 дня отпадает.

Ведущий 1: Остаётся 21 день, но ведь не весь день продолжаются занятия в школе, а не более четверти дня, поэтому ещё 15 дней отпадает.

Ведущий 2: Остаётся всего-навсего 6 дней. Так много ли времени вы проводите в школе?

З65 – 52 – 10 – 100 – 182 – 15 = 6 (данная запись на Слайде 21)

Ведущий 1: Есть о математике молва,

Что она в порядок ум приводит.

Потому хорошие слова

Часто говорят о ней в народе.

Выступление жюри, подведение итогов, вручение наград и грамот в номинациях:

- команда-победитель;

- лучший капитан команды;

- самая дружная команда;

- самый активный игрок команды;

- самый активный зритель.

Ведущий 2: Математика - жизни основа,

Она скучать не дает никогда

Математика в жизни и в школе –

Будем ей верны мы всегда!

Она нам мир объяснить помогает,

Она по жизни зовет, и ведет,

Кто с математикой в сердце шагает,

Тот никогда и нигде не пропадет.

Сегодня мы прошли все этапы, прежде, чем достигли итога. Завершая нашу работу, вспомним о названии нашей встречи: «Звездный час». Почему?......ответы учеников На наш взгляд сегодня каждый из вас узнал что-то новое и достиг своего звездного часа. У кого-то это получилось лучше, у кого-то немного хуже. Желаем вам не останавливаться на достигнутом, получать новые знания и каждому найти свою дорогу!