Элементы математического моделирования в школьном курсе информатики и ИКТ.

Элементы математического моделирования в школьном курсе информатики и ИКТ .

.

• .

• Объект исследования – элементы математического моделирования в школьном курсе информатики и ИКТ .

• Цель исследования – методическая поддержка темы «математическое моделирование».

Задачи :

• 1. Изучить теоретическую и методическую литературу по теме «Математическое моделирование».
• 2. Проанализировать тематическое планирование.
• 3. Рассмотреть типовые задачи по «Математическому моделированию» в школьном курсе информатики и ИКТ.

Развитие математического моделирования.

Математические модели – широкий класс знаковых моделей широко использующих те или иные математические методы.

Математическое моделирование – это описание, воспроизведение, изучение и прогнозирование всевозможных процессов и явлений с помощью математических и вычислительных средств.

Этапы построения математической модели:

• ВЫДЕЛИТЬ СУЩЕСТВЕННЫЕ ЭЛЕМЕНТЫ, ОПИСАННЫЕ В ЗАДАЧЕ;
• ОБОЗНАЧИТЬ ИХ;
• УСТАНОВИТЬ ОТНОШЕНИЕ МЕЖДУ ЭЛЕМЕНТАМИ И МАТЕМАТИЧЕСКИМИ ОПЕРАЦИЯМИ;
• ЗАПИСАТЬ С ИСПОЛЬЗОВАНИЕМ МАТЕМАТИЧЕСКОЙ СИМВОЛИКИ ЭТИ СООТНОШЕНИЯ.

Классификация математических моделей.

Математические модели классифицируют по различным признакам.

Общая классификация:

-дескриптивные (описательные) модели;

-оптимизационные модели;

-многокритериальные модели;

-игровые модели;

-имитационные модели.

РАСКРЫТИЕ ТЕМЫ В УЧЕБНОЙ ЛИТЕРАТУРЕ.

• Пропедевтический курс информатики.
• Базовый курс информатики (рассмотрены учебники: И.Г. Семакина, Н.Д. Угриновича, Л.Л. Босовой).
• Профильный курс информатики (рассмотрены учебники: Н.Д. Угриновича, С.А. Семакина).

Тематическое планирование.

• Учебник Л. Л. Босовой 7 класс.

№

Тема урока.

1

Параграф

Модели объектов и их назначение .

2

Информационные модели.

2.1

3

4

Словесные информационные модели.

2.2

Математические модели .

2.3

5

2.4

Табличные информационные модели.

6

Табличное решение логических задач.

2.5

7

8

2.6

Вычислительные таблицы.

Электронные таблицы.

2.7

9

2.8

Графики и диаграммы.

10

Схемы.

2.9

2.10

???

???

Страница 1

Страница 1

.

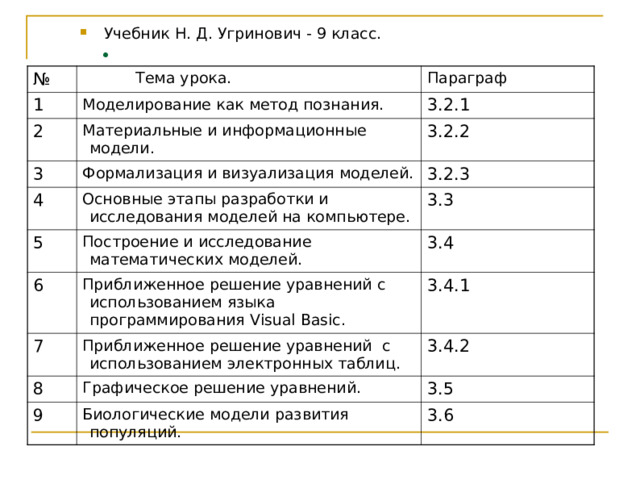
• Учебник Н. Д. Угринович - 9 класс.

№

Тема урока.

1

Параграф

Моделирование как метод познания.

2

3.2.1

Материальные и информационные модели.

3

3.2.2

Формализация и визуализация моделей.

4

5

3.2.3

Основные этапы разработки и исследования моделей на компьютере.

6

Построение и исследование математических моделей.

3.3

Приближенное решение уравнений с использованием языка программирования Visual Basic.

3.4

7

3.4.1

8

Приближенное решение уравнений с использованием электронных таблиц.

9

Графическое решение уравнений.

3.4.2

3.5

Биологические модели развития популяций.

3.6

???

???

Страница 1

Страница 1

.

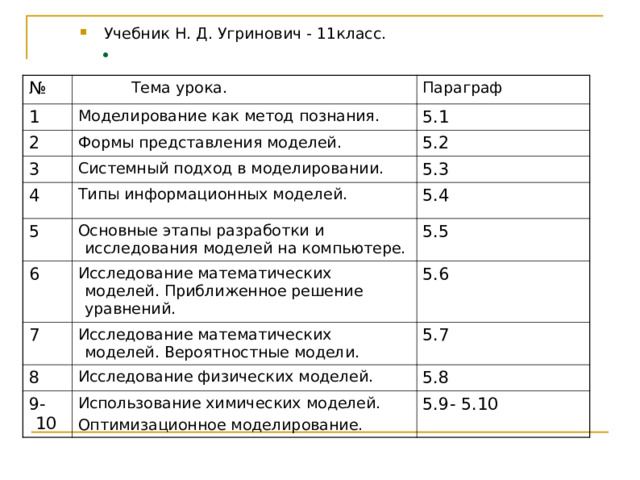
• Учебник Н. Д. Угринович - 11класс.

№

Тема урока.

1

Параграф

Моделирование как метод познания.

2

5.1

Формы представления моделей.

3

5.2

Системный подход в моделировании.

4

5

5.3

Типы информационных моделей.

6

Основные этапы разработки и исследования моделей на компьютере.

5.4

Исследование математических моделей. Приближенное решение уравнений .

5.5

7

5.6

8

Исследование математических моделей. Вероятностные модели.

9-10

Исследование физических моделей.

5.7

5.8

Использование химических моделей.

Оптимизационное моделирование.

5.9- 5.10

???

???

Страница 1

Страница 1

Типовые задачи по «Математическому моделированию».

• Информационное моделирование с использованием таблиц;
• Математическое моделирование с использованием электронных таблиц ( Microsoft Excel) ;
• Математическое моделирование с использованием языков программирования ( В частности Pascal) ;
• Исследование математических моделей: (Приближенное решение уравнений и приближенное вычисление площадей);
• Моделирование задач оптимального уровня;
• Моделирование искусственного языка.

= 0 . " width="640"

Задача : «На шоссе расположены пункты А и В, удаленные друг от друга на 20 км. Мотоциклист выехал из пункта В в направлении, противоположном А, со скоростью 50 км/ч»

Для решения составим математическую модель, описывающую положение мотоциклиста относительно пункта А через t часов.

Решение: За t часов мотоциклист пройдет 50 t км и будет находиться от А на расстоянии 50 t км + 20км. Обозначим s – расстояние мотоциклиста до пункта А, тогда зависимость этого расстояния от времени движения можно выразить формулой: s = 50 t + 20, где t= 0 .

Задача: «Найдите в электронных таблицах корень уравнения x – sin x = 0 приближенными методами.»

3

• Решение: В электронных таблицах определим корни уравнения.
• 1.В диапазон ячеек В1 : В2 ввести значение аргумента функции от -1,4 до 1,4 с шагом 0,2.
• 2.В ячейку В2 ввести формулу вычисления значений функции =В1 ^3-SIN(B1) и скопируем ее в диапазон ячеек С2 : Р2
• 3.Для грубо приближенного определения корней ур-ия постройте диаграмму типа График.
• 4.По графику видно корни: х1=-0,9; х2=0; х3=0,9.

1

A

2

B

х

C

-1,4

Y=x ³ –sinx

-1,8

D

-1,2

-1.0

-0,8

E

-0,2

-0,8

F

0,2

-0,6

G

0,3

-04

H

-0,2

0,3

I

0,2

0

J

K

0,2

0

L

0,4

-0,2

-0,3

0,6

M

-0,3

0,8

N

O

-0,2

1,0

0,2

P

1,2

1,4

0,8

1,8

ЗАДАЧА: « ВЫЧИСЛИМ ЧАСТНОЕ ДВУХ ЧИСЕЛ ».

• Решение.
• На ноль делить нельзя, следовательно, делитель не равен нулю.. a / b , b =0.
• Реализуем нашу задачу на языке программирования Turbo Pascal .
• Program delenie;
• Var
• a, b: integer;
• Rezult : real ;
• Begin
• Write (‘Введи значение делимого а ‘);
• Read (а);
• Write (‘Введи значение делителя b ‘);
• Read ( b );
• If b =0 then writeln (‘На ноль делить нельзя ‘ );
• Else
• Begin
• Rezult: = a/b;
• Writeln (‘ Частное чисел ‘, а,’ и ‘, b ,’ = ’, Rezult );
• End ;
• End .
• Запустим программу на выполнение ( Ctrl + F 9) и получим результаты. Если есть ошибки – устраняем их.

• Метод математического моделирования – выполняет развивающую функцию, поскольку при его изучении уч-ся продолжают знакомство еще с одним методом познания окружающей действительности.

• В ходе изучения математического моделирования формируется системно-информационная, научная картина мира.
• Поставленные нами задачи были выполнены. К сожалению, были рассмотрены не все методические вопросы и не все задачи, но это станет темой других работ.

Спасибо

за внимание.